
|
|
|
Subiectul I
A. Mecanica
1)
![]() definirea conform
manualului (vezi relatia. de la breviar, pag. ). [a]SI = [m/s2]
nu este marime fundamentala a Sistemului International de
unitati (S.I.) a = a
definirea conform
manualului (vezi relatia. de la breviar, pag. ). [a]SI = [m/s2]
nu este marime fundamentala a Sistemului International de
unitati (S.I.) a = a
2)
Oy: G = N; ![]() , Oy:
, Oy: ![]() ;
; ![]() ,
, ![]() :
: ![]()
F =
G: ![]()
![]()
![]() a gresit Bogdan
a gresit Bogdan
B. Optica
1) ![]()
![]() :
: ![]() ;
; ![]() ; [C]SI = ID (Dioptria nu este unitatea
fundamentala a
; [C]SI = ID (Dioptria nu este unitatea
fundamentala a
S.I.
2)
![]() ;
; ![]()
![]()
![]() .
. ![]()
![]()
![]()
![]() f = 50 cm.
f = 50 cm.
![]() . Corect b.
. Corect b.
Subiectul II. Fizica moleculara si termodinamica
1)
![]() sau
sau 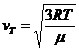 Definirea conform manualului. [T]SI = [K] (gradul
Kelvin este unitate fundamentala a S.I.) .
Definirea conform manualului. [T]SI = [K] (gradul
Kelvin este unitate fundamentala a S.I.) .
2)
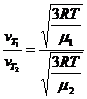
![]()
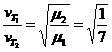 ;
; 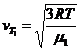 ,
, 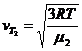
![]()
![]() ,
,![]() .
.
Subiectul III. Electricitate si magnetism
1)
![]()
![]() Definirea conform
manualului. [L]SI = [H], Henry(H) nu este unitate fundamentala a S.I.
Definirea conform
manualului. [L]SI = [H], Henry(H) nu este unitate fundamentala a S.I.
2)
![]() : L = L1 + L2.
: L = L1 + L2.
Subiectul IV
1) Enuntul primului
postulat conform manualului ![]() ħ [L]SI
= [J.s] nu este unitate
fundamentala a S.I.
ħ [L]SI
= [J.s] nu este unitate
fundamentala a S.I.
2![]()
![]() r1 = 53 pm; r2 = 212 pm; r3 = 477 pm; r4 = 848 pm; r5
= 1325 pm,
r1 = 53 pm; r2 = 212 pm; r3 = 477 pm; r4 = 848 pm; r5
= 1325 pm, ![]() a calculat gresit
Eugen.
a calculat gresit
Eugen.
B Fizica cuantica
1)
![]()
![]() : 1u = 1,67.10-27 kg ( nu este unitate
fundamentala a S.I.)
: 1u = 1,67.10-27 kg ( nu este unitate
fundamentala a S.I.)
2)
N = A - Z
= 246 Caremen; QN = Z.e = 1,47.10-17 C Daniel ![]() Bogdan.
Bogdan.
Sesiunea August 1999
A. Mecanica
1) ![]() , [L]SI = [J.s]; J.s - nu este unitate fundamentala a S.I. Definitia
momentului cinetic conform manualului.
, [L]SI = [J.s]; J.s - nu este unitate fundamentala a S.I. Definitia
momentului cinetic conform manualului.
3)
![]()
![]() F = 0,015 N, [F]SI = [N], Eugen a obtinut rezultatul eronat.
Lmax = 67,5 J.s.
F = 0,015 N, [F]SI = [N], Eugen a obtinut rezultatul eronat.
Lmax = 67,5 J.s.
B. Optica
Definirea reflexiei conform
manualului, i = r si ![]() [I]SI = 1 Candila
[I]SI = 1 Candila ![]() Definirea acestei
unitati fundamentale conform manualului
Definirea acestei
unitati fundamentale conform manualului
i = 45o ![]()
![]() . Daniala este cea care a obtinut rezultatul corect. iB = 90o.
. Daniala este cea care a obtinut rezultatul corect. iB = 90o.
Subiectul II Fizica moleculara si termodinamica
Definirea masei molare a unei
substante conform manualului.
Definirea masei molare relative a unei substante conform manualului. ![]()
![]() nu este unitate
fundamentala in S.I.
nu este unitate
fundamentala in S.I. ![]() . 40% H2; 20% Ar.
. 40% H2; 20% Ar.
Subiectul III
Definirea rezistentei
conform manualului. ![]() ,
, ![]() Definirea ohmului
conform manualului. Ohmul (
Definirea ohmului
conform manualului. Ohmul (![]() ) nu este unitate fundamentala in S.I. Enuntul
legii lui Ohm conform manualului.
) nu este unitate fundamentala in S.I. Enuntul
legii lui Ohm conform manualului.
Circuitul reprezentat
schematic este aratat in figura ![]()
![]() ;
; 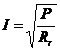 ,
, ![]() ,
, ![]()
![]()
![]()
![]()
![]() .
.
Subiectul IV
A. Fizica atomica
Definirea electronvoltului ![]() Energia unui electron
accelerat la o tensiune de 1 V. eV
Energia unui electron
accelerat la o tensiune de 1 V. eV ![]() nu este marime
fundamentala in S.I. Ec
= e.U = 1,6.10-19.20. 103
= 3,2.10-15 J.
nu este marime
fundamentala in S.I. Ec
= e.U = 1,6.10-19.20. 103
= 3,2.10-15 J.
![]() ;
; ![]() . Carmen a obtinut rezultate incorecte.
. Carmen a obtinut rezultate incorecte.
B. Fizica nucleara:
Indicarea semnificatiei
numarului atomic Z. Indicarea
semnificatieie numarului de masa A. N![]() numarul de neutroni N
= A -Z. definirea constantei radioactive conform manualului S-1
numarul de neutroni N
= A -Z. definirea constantei radioactive conform manualului S-1 ![]() nu este unitate
fundamentala a S.I. Bogdan Wleg
= B.A164 GeV. sarcina
electrica a nucleului. Adriana Q = Z.e
= 1,6.10-19. 84 1,34.10-17 C. Timpul de imjumatatire
nu este unitate
fundamentala a S.I. Bogdan Wleg
= B.A164 GeV. sarcina
electrica a nucleului. Adriana Q = Z.e
= 1,6.10-19. 84 1,34.10-17 C. Timpul de imjumatatire ![]() .
.
RASPUNSURI. BACALAUREAT. TESTUL I
SUBIECTUL I:
A. MECANICA: 1.a) Confom manualului.b) v=12m/s .
2.a) L=-10 J. P=28 kW.
B.
OPTICA 1.a) Conform manualului
; b)![]()
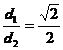
2. a) Conform manualului. C=2,5d
1.a) Conform manualului; 2.a) Conform manualului.![]() ;
;
a)
Conform
manualului. ![]()
1. Conform manualului. a) I1=30 mA; b) r=1W
SUBIECTUL IV: A)FIZICA ATOMICA
1.
Conform
manualului. 2.a) ![]()
![]() b) E=2,17.10-18J
b) E=2,17.10-18J
A. FIZICA NUCLEARA
1.
Conform
manualului. a)![]() b)
b) ![]()
![]()
RASPUNSURI. BACALAUREAT. TESTUL 2
SUBIECTUL I: A. MECANICA:
 1.a) Confom manualului. b)
1.a) Confom manualului. b)![]()
![]()
2.a) ![]() ; b)
; b) ![]()
![]() ;
; ![]()
B. OPTICA.
1.a) Conform manualului.b)![]()
![]()
![]()
2.Formula
fundamentala conform manualului. ![]()
C(Capacitate calorica ![]() ),cv(caldura specifica izocora
J/kg.K),V(Volum m3),CV(Caldura molara la volum
constant J/kmol K)
),cv(caldura specifica izocora
J/kg.K),V(Volum m3),CV(Caldura molara la volum
constant J/kmol K)
2.a) ![]() ;
;![]() .
.![]()
![]()
![]()
b) ![]()
1. F[Fluxul
magnetic].![]() ,Weber, L[Inductanta].
[L]Si=H,Henry, B[Inductanta magnetica]. [B]SI=T, Tesla.
R [Rezistenta electrica].[R]SI=W,Ohm.
,Weber, L[Inductanta].
[L]Si=H,Henry, B[Inductanta magnetica]. [B]SI=T, Tesla.
R [Rezistenta electrica].[R]SI=W,Ohm.
2.a)![]()
![]() Regula lui Lenz.(Regula mainii drepte)
Regula lui Lenz.(Regula mainii drepte)
b)![]()
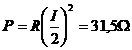
1.![]() , Conform manualului. 2.a)
, Conform manualului. 2.a)![]() ,
,![]()
b)![]()
![]()
![]()
1.![]() ,
, ![]()
![]()
2.a)![]()
![]() ,
,![]()
b) Conform manualului
1. ![]() si
si ![]() , de unde
, de unde
![]() Corect
b).
Corect
b).
Fig. R.1
2. Notam
cu H distanta parcursa
si t timpul total de
cadere, astfel ca: ![]() si
si ![]() , de unde
, de unde ![]() =3 465 m. Corect a.
=3 465 m. Corect a.
3. Prin
asezarea caporalului pe obuz viteza comuna secalculeaza cu
relatia:![]() .
. ![]() Corect d.
Corect d.
4.
Ciclistul se deplaseaza pe cercul de raza r pentru care forta centrifuga este egala cu
forta de frecare, adica: ![]() , de unde
, de unde 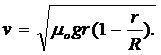 Valoarea maxima
se obtine anuland derivata lui v(r)
in functie de r:
Valoarea maxima
se obtine anuland derivata lui v(r)
in functie de r: 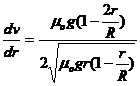 = 0, de unde
= 0, de unde ![]() si
si ![]() . Corect
c.
. Corect
c.
5. Sistemul
are viteza maxima in pozitia de echilibru in care tensiunea in cel
doua resorturi este aceeasi, adica ![]() , unde
, unde ![]() . Din aceste relatii obtinem:
. Din aceste relatii obtinem:
![]() si
si ![]() . Din
teorema conservarii energiei initiala si de echilibru,
. Din
teorema conservarii energiei initiala si de echilibru, ![]() , de unde
, de unde ![]() . Corect
a.
. Corect
a.
6. Corpul care se ciocneste pleaca cu
aceeasi viteza v dupa
o directie ce face unghiul 2a cu planul orizontal si cade la distanta ![]() . Corpul care ciocneste neelastic pleaca cu viteza
. Corpul care ciocneste neelastic pleaca cu viteza ![]() dupa
directia care face unghiul a cu planul orizontal si cade la distanta
dupa
directia care face unghiul a cu planul orizontal si cade la distanta ![]() . Din conditia ca d1=d2 rezulta
. Din conditia ca d1=d2 rezulta ![]() . Corect c.
. Corect c.
7. In
punctul O corpul de masa m
in cadere libera atinge viteza ![]() . Intre talerul de masa M si corpul de masa
m are loc o ciocnire plastica. Din legea de conservare a impulsului se
obtine viteza sistemului corp-taler.
. Intre talerul de masa M si corpul de masa
m are loc o ciocnire plastica. Din legea de conservare a impulsului se
obtine viteza sistemului corp-taler.
![]() (1)
(1)
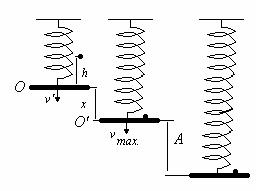 Datorita faptului ca pe taler ramane
corpul de masa m are loc
deplasare pozitiei de echilibru in jurul careia are loc miscare
oscilatorie a sistemului corp-taler din O in O . In unctul O dupa ciocnirea plastica sistemul
corp-taler are energie cinetica si energie potentiala.
Datorita faptului ca pe taler ramane
corpul de masa m are loc
deplasare pozitiei de echilibru in jurul careia are loc miscare
oscilatorie a sistemului corp-taler din O in O . In unctul O dupa ciocnirea plastica sistemul
corp-taler are energie cinetica si energie potentiala.
![]() ;(2) mg=kx (3) (Alungirea x se datoreaza geutatii mg)
;(2) mg=kx (3) (Alungirea x se datoreaza geutatii mg)
In punctul de amplitudine maxima sistemul corp-taler are numai energie potentiala.
![]() (4)
(4)
Se scrie legea de conservare a energiei:
Fig.R.7
![]() (5). (Acasta relatie s-a obtinut inlocuind in relatia
(2) relatiile (1) si(3)
(5). (Acasta relatie s-a obtinut inlocuind in relatia
(2) relatiile (1) si(3)
Din relatia (5) se obtine: 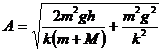
8. ![]() , de unde n= 2,5. Corect b.
, de unde n= 2,5. Corect b.
9. Masa de
oxigen care poate fi utilizata este: ![]() , unde
, unde ![]() . Astfel,
. Astfel, ![]() . Corect b.
. Corect b.
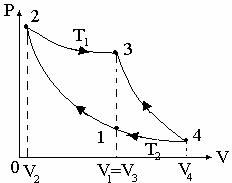
10. ![]() Aria ciclului Carnot
este egala cu lucru mecanic efectuat pe un cilcu, adica:
Aria ciclului Carnot
este egala cu lucru mecanic efectuat pe un cilcu, adica:
Fig. R.10
![]() . Din ecuatiile transformarilor,
. Din ecuatiile transformarilor, ![]() , deci
, deci ![]() . Dar, din transformarea 1-2,
. Dar, din transformarea 1-2, 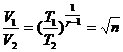 , adica
, adica ![]() . Astfel,
. Astfel, ![]() = 4 300 J. Corect e.
= 4 300 J. Corect e.
11. Densitatea
unui gaz, scrisa utilizand ecuatia termica de stare, este: 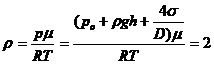 kg/m3 . Corect
c.
kg/m3 . Corect
c.
12. ![]() , de unde
, de unde ![]() ; randamentul
; randamentul ![]() ;
; ![]() kJ. (fig.
R.10) Corect e.
kJ. (fig.
R.10) Corect e.
13. ![]() , deoarece
, deoarece ![]() Corect
e.
Corect
e.
14. Aria
ciclului este egala cu ![]() . Din
. Din ![]()
![]() ,
, ![]() , rezulta ca
, rezulta ca ![]() , iar din
, iar din 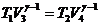 , obtinem ca
, obtinem ca ![]() . Astfel,
. Astfel, 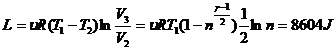 (fig. R.10). Corect
c.
(fig. R.10). Corect
c.
15.Din
figura se observa ca:![]()
![]()
de unde ![]() iar
iar ![]()
Corect c.
16. ![]() , unde
, unde ![]() , cu
, cu ![]() astfel incat
astfel incat ![]() =3,37 10-9
s. Corect d.
=3,37 10-9
s. Corect d.
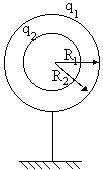 17. Sfera exterioara fiind
legata la pamant, potentialul ei este nul:
17. Sfera exterioara fiind
legata la pamant, potentialul ei este nul: ![]() ,deci
,deci![]() ,dar
,dar ![]()
In al doilea caz,din aceleasi considerente,![]() ,
,
astfel incat
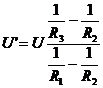 = 105 V. Corect
d. Fig.R.17
= 105 V. Corect
d. Fig.R.17
18. Din ![]() ,
, 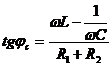 si
si ![]() rezulta:
rezulta: ![]() de unde C= 48,7 10-6
F. Corect c.
de unde C= 48,7 10-6
F. Corect c.
19. ![]() a carei valoare
maxima se obtine din conditia:
a carei valoare
maxima se obtine din conditia: ![]() =0, de unde R=nr.
Deci,
=0, de unde R=nr.
Deci, ![]() . Corect c.
. Corect c.
20. In
timpul t tija matura
unghiul la centru![]() si suprafata
si suprafata ![]() . Fluxul magnetic care traverseaza aria spirei in
intervalul de timp t este:
. Fluxul magnetic care traverseaza aria spirei in
intervalul de timp t este: ![]() , iar tensiunea electromotoare indusa,
, iar tensiunea electromotoare indusa, ![]() Corect
c.
Corect
c. ![]()
![]()
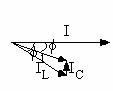 21. Conform diagramei fazoriale,
21. Conform diagramei fazoriale, ![]() , unde
, unde ![]()
![]() ;
; ![]()
![]()
![]() , de unde
, de unde ![]() Corect c. Fig.R 21
Corect c. Fig.R 21
22.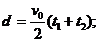 (1)
(1) 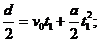 (2)
(2) ![]()
![]()
![]() (3) introducand rel. (3)in rel. (2)
(3) introducand rel. (3)in rel. (2)![]() (4)
(4)
inlocuind d din rel (4) in rel.(1)![]()
![]()
23. Din legea de conservare a energiei in punctele A si B:
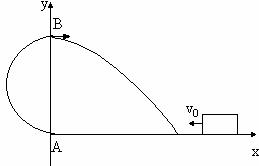
![]()
![]()
![]() ,
,
OX; x=vt=t
![]()
OY; y=![]() .Ajungand pa axa OX y=0
.Ajungand pa axa OX y=0
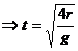 ;
;
![]()
![]() cand
cand
Fig.R.23
(x)1=0![]()
24.![]() .
.
25. Din
conservarea de energie a unui sistem coservativ se scie: ![]()
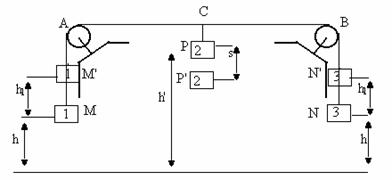
![]() ;
; ![]()
Considerand,neglijabila distanta PC
Din DACP ![]() ,
,
AP'=d/2+h1, AC=d/2, PP'=s.
(d/2+h)2=(d/2)2+s2
![]() (1)
(1)
Fig. R.25
![]() (2), Inlocuind rel (2) in rel.(1)
(2), Inlocuind rel (2) in rel.(1)![]()
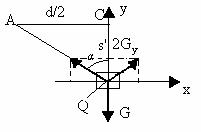 26. Pe axa Oy;
26. Pe axa Oy;
![]() .
.
Din ![]() ,
,
![]()
Fig. R.26
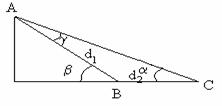 27.
27. ![]()
![]() (1)
(1)
In ![]() se aplica teorema
sinusurilor:
se aplica teorema
sinusurilor: ![]() T
T![]() (2) Fig. R.27
(2) Fig. R.27
Din rel. (1)si (2)Tm=tg.a
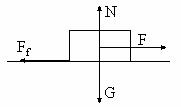
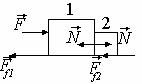
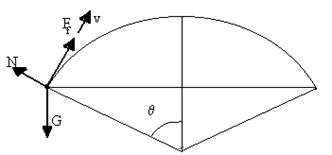 28. Autoturismul se considera a fi un corp punctiform
care dupa cum se observa in desenul de mai jos se afla la intrarea pe pod. Toate
rotile fiind motoare fortele de frecare sunt orientate in sensul deplasarii
.!!!In cazul rotilor nemotoare fortele de frecare ar fi orientate in
sens opus deplasarii.
28. Autoturismul se considera a fi un corp punctiform
care dupa cum se observa in desenul de mai jos se afla la intrarea pe pod. Toate
rotile fiind motoare fortele de frecare sunt orientate in sensul deplasarii
.!!!In cazul rotilor nemotoare fortele de frecare ar fi orientate in
sens opus deplasarii.
In cazul acesta se poate scrie:
![]()
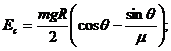
![]() . Fig. R.28
. Fig. R.28
29.Se poate
vorbi de un poligon regulat cu 12 laturi inscris intr-un cerc, in care ![]()
![]() . La momentul initial (fig. R.29 a) lungimea
fiecarui resort este:
. La momentul initial (fig. R.29 a) lungimea
fiecarui resort este: ![]() unde R0 este raza cercului.La
momentul ulterior, cand sistemul este
comprimat, raza cercului devenind R<R0,lungimea fiecarui
resort comprimat este:
unde R0 este raza cercului.La
momentul ulterior, cand sistemul este
comprimat, raza cercului devenind R<R0,lungimea fiecarui
resort comprimat este: ![]()
In figura R29b este prezentat un singur corp din sistem unde sunt reprezentate fortele elastice ce actioneaza asupra sa datorita comprimarii resorturilor:
![]()
Miscarea corpului se realizeaza sub actiunea rezultantei Fe data de relatia:
![]() ;
; ![]()
![]() .
.
In final rezulta :
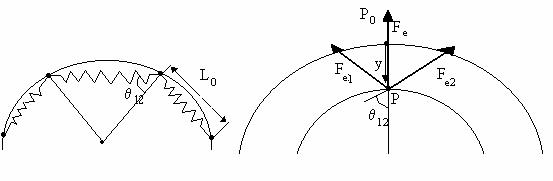
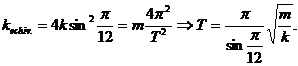
Fig.R30 Fig. R.32
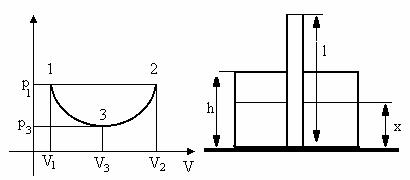
30.
L=Aria dreptunghiului V1-1-2-V2- Aria semicercului 1-3-2.
Aria dreptunghiului V1-1-2-V2=p1![]() , Aria semicercului 1-3-2=
, Aria semicercului 1-3-2=![]()
L=7,29.102 J.
31. ![]() ;
; ![]()
32. Starea de echilibru 1 este caracterizata de parameterii; po, V0=hs,T. Starea de echilibru 2 este caracterizata de parameterii; p=p0+rg(L-x),V=(h-x)s,T.
1 2TTransformare izoterma: pohs=[p0+rg(L-x)](h-x)sT![]() Ts=6,3 cm.
Ts=6,3 cm.
33. Intre st. initiala si stare in care nivelul lichidului in tub este zero are loc o transformare izocora.
![]()
![]() ;
;![]()
![]() T
T
T![]()
![]() Dar
Dar ![]()
![]() .
.
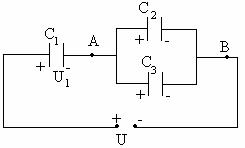
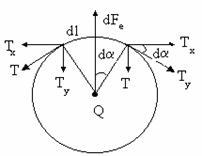
Fig.R.34 Fig. R. 35
35.Fiind incarcate intai C1 serie cu C2 la
tensiunea U, sarcina initiala pe acesti condensatori este: 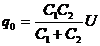 . Sarcina cu care se incarca initial condensatorul
C3 la tensiunea U este
. Sarcina cu care se incarca initial condensatorul
C3 la tensiunea U este ![]()
Ecuatiile ce descriu circuitul, dupa conectarea lui C3 la stabilirea echilibrului electrostatic sunt:
![]() (1)
(1)
![]()
A treia ecuatie care face
bilantul sarcinii in punctul A este: ![]() .(3) Semnul +"
corespunde situatiei cnd condensatorul C3 este conectat cu
amatura incarcata pozitiv in A. Semnul corespunde situatiei cnd condensatorul C3
este conectat cu amatura incarcata negativ in A.
.(3) Semnul +"
corespunde situatiei cnd condensatorul C3 este conectat cu
amatura incarcata pozitiv in A. Semnul corespunde situatiei cnd condensatorul C3
este conectat cu amatura incarcata negativ in A.
Pentru situatia
prezentata in fig. R.14 ![]()
36. Notand cu r
rezistenta interna a bateriei si cu l distanta pana la locul strapungerii, se aplica legea lui Ohm pentru
circuitul a: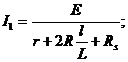 Pentru circuitul b:
Pentru circuitul b: 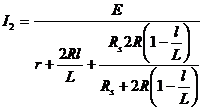 ;
;
Pentru situatie de scurtcircuit legea lui Ohm
este: ![]() .
.
Din cele trei ecuatii
rezulta:![]()
![]() T
T
T![]() si
si ![]() T
T![]() si
si![]()
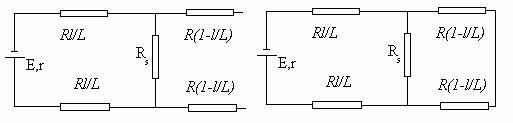
Fig.R.36a
Fig.36b
Din cele trei ecuatii
rezulta:![]()
![]() T
T
T![]() si
si ![]() T
T![]() si
si![]()
37. ![]()
![]() ,
,![]()
de unde; ![]() . Conditia D 0 da
. Conditia D 0 da ![]() , dar
, dar![]() Pentru q =p/6 si
m=6 linii ionul de He se excita
pe nivelul 4. In aceasta situatieT
Pentru q =p/6 si
m=6 linii ionul de He se excita
pe nivelul 4. In aceasta situatieT ![]()
38. Poate emite numai ![]() :
: ![]() .
.
Deci ![]()
39. In
conditiile in care bara parcursa de un curent electric alternativ de
intensitate momentana![]() , este perpendiculara pe directia inductiei
magnetice in intrefierul bobinelor, atunci forta electromagnetica ce
actioneaza asupra barei are valoarea:
, este perpendiculara pe directia inductiei
magnetice in intrefierul bobinelor, atunci forta electromagnetica ce
actioneaza asupra barei are valoarea:
![]() .
.
Pentru ca oscilatorul mecanic
sa intre in rezonanta este necesar ca 2w w0=![]() ,de unde frecventa
curentului alternativ pentru care se
obtine aceasta rezonantaeste;
,de unde frecventa
curentului alternativ pentru care se
obtine aceasta rezonantaeste; ![]()
40. Inductanta ansamblului format de cele doua bobine are valoarea:
![]() H.
H.
Amplitudinea
intensitatii curentului alternativ prin bobine este![]() Iar amplitudinea inductiei magnetice in intrefierul
bobinelor este
Iar amplitudinea inductiei magnetice in intrefierul
bobinelor este![]()
Rezulta ca deplasarea pozitiei de echilibru este data de sensul fotei electromagnetice, deci depinde de modul de conectare a barei intre ecestea. Deplasarea pozitiei de echilibru a barei in cazul conectarii la sursa de curent alternativ este:
![]()
1998 F8B Universitatea Transilvania din Brasov
1b; 2d; 3d; 4d; 5c; 6c; 7e; 8c; 9a; 10b; 11c; 12b; 13e; 14 e; 15 b; 16 c; 17 d; 18 e; 19 c; 20 d.
1998 Universitatea "Transilvania" din Brasov
1e; 2.b; 3c; 4b; 5a; 6d; 7c; 8B, 9d; 10e; 11b; 12b; 13c; 14a; 15e; 16b; 17d; 18e; 19e; 20 e.
T.3 MF3A - 1999
1.c; 2. b; 3. c; 4. d; 5. a; 6. d; 17. b; 8. b.
F1A Fizica Chimie, Brasov, 1999
1. c; 2. B; 3. D; 4. B; 5. C; 6. C; 7. A; 8. B; 9.c; 10. ; 11. ; 12. ; 13. B; 14. C; 15. D; 16. B; 17. C; 18.c.
1999 Brasov, Facultatea de Medicina.
1.c; 2.b; 3. A; 4. C, 5. D; 6. D; 7. A; 8. C; 9. C; 10. D; 11. B; 12. B; 13. C; 14. C; 15. D; 16.. b; 17. C; 18. A; 19. D; 20. C; 21. B; 22. C; 23. B; 24. A; 25. A; 26. B; 27.a.
Medicina Bucuresti, 1997
1. e; 2. B; 3. D; 4. C; 5. C; 6. C; 7. E; 8. D; 9. A; 10. B; 11. A; 12. D; 13. C; 14. D; 15 b; 16. C; 17. A; 18. E; 19. B; 20. D; 21. A; 22. C; 23. C; 24. D; 25. A; 26. E; 27. A ; 28. D; 29. D; 30. E; 31. A; 32. C; 33. C; 34. D; 35. A; 36. A; 37. D; 38. C; 39. B; 40. D; 41. D; 42. E; 43. E; 44. B.
1. Hristev, A., Borsan, D., Manda, D., Sandu, M., Georgescu, L., Gherbanovschi, L., - Probleme de Fizica pentru cl. IX-X. Editura Didactica si Pedagogica. R.A . Bucuresti 1996.
2. Vladuca, Gh., Gherbanovschi, N., Melnic, M., Ciobotaru, D., Munteanu, I., Rusu, A., I. Vita - Probleme de Fizica pentru cl. XI-XII. Editura Didactica si Pedagogica, Bucuresti 1983
3. Cone Gabriela, Stanciu, Gh., Tudorache, St. - Probleme de Fizica pentru liceu - Editura ALL -1996
4. Sandu, M., -Probleme de Fizica - Editura Scrisul Romanesc Craiova -1987.
5. Druica Zeletin, I., Popescu, A., - Probleme de mecanica si acustica.- Editura Tehnica -1974.
6. Manualele de fizica pentru liceu, editiile in vigoare.