Plansee caseta

Plansee caseta

Block floors are part of the network floor beams. They are characterized in that beams after the two directions have the same width and height of the section. If the beams are distributed oblique to the contour, the floor is called the network, if the beams are distributed parallel to the sides of the boundary contour, the floor is called a cassette. 1.5. Are set to use when opening the report of what is to be covered is 500 daN/m2 In this situation are more economical than any type of floor condition that p. Beam distribution is so l1/l2 be as close to one. Inter axle beams is in the range 1.5 to 3 meters, the floor is more aesthetic as the axis is less international.

Ascultati

Cititi fonetic

Floor plate and the elastic is calculated as follows l1/l2 1.5 To calculate the minimum and maximum bending moments of the plate is considered loaded fields all over them with permanent load g and the useful load p acting in chess. In this regard it is considered two conventional schemes and boundary loading. The plate is considered simply rest on the outer contour and supports that are embedded in the network of beams. Every eye type of plate boundary results in the figure.

Be calculated for each type of plate distinct M1 and M2 (bending moments in the field after the two directions), used to calculate the lower reinforcement and bending moments on the supports as well as two ways to calculate the upper reinforcement

.

Network of beams is calculated also in elastic beams resting easy considering the ends and loaded with concentrated forces at the nodes. So are statically determined beams outside, but the network is static indefinite beams inside. A node inside the network and focused work force that consists of loading Pi plate and transmitted to simplify the calculation, all the force concentrated weight of the two beams and corresponding node

STEP 6. Calculation of floor plate cassette

6.1 Establishment of floor geometry

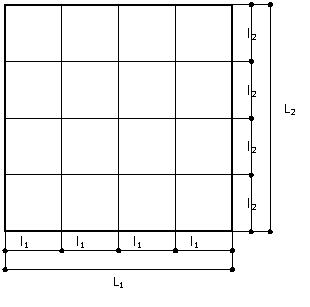L₁, L₂ si p se cunosc din datele proiectului

L₁=11.70 m

L₂=11 m

P_n^B=550-10*6=490 daN/m

l₁=L₁/4 =2.925 (m);

l₂=L₂/4 =2.75(m);

h_p=(1/40--1/45)max(l₁;l₂)=0.065m=6.5cm

h_{p min}=7 cm

h_p=7 cm

6.2 Design cassette floor beams

h_min=L₁/20 (max. 60 cm)=1162/20=58.5 h=60cm

b= 30 cm, astfel incat 1.5 h/b 3

1.52 3

6.3 Establishment charges

1.     6.4 The calculation of static

2.    Panels is considered embedded in the intermediate bearings and rest on simple contour. On the surface of all panels apply a conventional load directed from the top down, which has value q '= g + p / 2 = 759 (daN/m2)

Panels is considered simply rest on all accounts and loaded
p / 2 = 245 (daN/m2) q =

q”= p/2=245 (daN/m²) . q’ q”

Caseta de tip 1Tl=l₂/l₁=2.75/2.925=0.940T a₁₁=0.0329,a₁₂=0.0403;b₁₁=0.4489_, b₁₂=0.5511

Caseta de tip 4T l=l₂/l₁ =0.940 T a₄₁=0.0242_, a₄₂ =0.0297; b₄₁=0.4489_, b₄₂=0.5511

Caseta de tip 5 T l=l₂/l₁=0.940 T a₅₁=0.0209_, a₅₂ =0.0224:b₅₁=0.6196_, b₅₂=0.3804

Caseta de tip 5’ T l=l₁/l₂=0.940 T a₅₁=0.0153_, a₅₂=0.0257 ; b₅₁=0.2546_, b₅₂=0.7454

Caseta de tip 6 T l=l₂/l₁ =0.940 T a₆₁=0.0161_, a₆₂=0.0198 ; b₆₁=0.4489_, b₆₂=0.5511

6.4.1 Calculation of maximum and minimum moments

Caseta de tip 4 M₄₁=a₄₁q’l₁² a₁₁q”l₁² = 226.11 (daNm)

=88.18 (daNm)

M₄₂=a₄₂q’l₂² a₁₂q”l₂²=245.15(daNm)

=95.8 (daNm)

Caseta de tip 5   M₅₁=a₅₁q’l₁² a₁₁q”l₁²=204.68 (daNm)

=66.75 (daNm)

M₅₂=a₅₂q’l₂² a₁₂q”l₂²=203.24 (daNm)

=53.91 (daNm)

Caseta de tip 5’ M₅₁=a₅₁q’l₁² a₁₁q”l₁² =168.31 (daNm)

=30.39(daNm)

M₅₂=a₅₂q’l₂² a₁₂q”l₂²=222.18 (daNm)

=72.84 (daNm)

Caseta de tip 6 M₆₁=a₆₁q’l₁² a₁₁q”l₁² =173.51(daNm)

=35.58(daNm)

M₆₂=a₆₂q’l₂² a₁₂q”l₂²=188.31 (daNm)

=38.98 (daNm)