PERCENTILE

Marimile tendintei centrale furnizeaza informatii despre multimi de scoruri. In anumite cazuri insa, cercetatorul poate fi interesat de descrierea pozitiei unui scor individual in raport cu celelalte scoruri dintr-o distributie. Daca, de pilda, un subiect a obtinut scorul 47 la un test de cunostinte, semnificatia acestui scor poate fi explicata inclusiv in termenii numarului de subiecti din esantionul considerat care au obtinut scoruri mai mici decat 47.

Pozitia unui scor individual intr-o distributie poate fi determinata cu ajutorul percentilelor. Cea de-a m-a percentila a unei multimi de scoruri, P_m, este valoarea fata de care cel mult m% din scoruri sunt mai mici decat m si cel mult (100 - m)% din scoruri sunt mai mari decat m. Intrucat mediana unei multimi de scoruri este valoarea fata de care cel mult 50% din scoruri sunt mai mici si cel mult 50% din scoruri sunt mai mari, mediana este cea de-a 50-a percentila a acelei multimi. Tot asa cum exista un nume special pentru cea de-a 50-a percentila a unei multimi de scoruri, exista nume speciale pentru percentilele care impart o multime ordonata de scoruri in sferturi si in zecimi: cuartile[1] si, respectiv, decile. Lista urmatoare prezinta cele mai utilizate percentile, impreuna cu simbolurile uzuale pentru cuartile si decile (considerand ca este vorba despre o multime de scoruri ordonata crescator):

D₁ = Prima decila = P₁₀

Q₁ = Prima cuartila = P₂₅

Q₂ = A doua cuartila = P₅₀ =

Q₃ = A treia cuartila = P₇₅

D₉ = A noua decila = P₉₀

Pentru ilustrare, fie urmatoarea multime ordonata de 15 scoruri:

2, 4, 4, 5, 7, 8, 10, 12, 17, 18, 18, 21, 27, 29, 30

Q₁ Q₃

Prima cuartila este valoarea fata de care cel mult 25% din scoruri, i.e. cel mult (15/100)25 = 3,75 scoruri sunt mai mici si cel mult 75% din scoruri, i.e. cel mult (15/100)75 = 11,25 scoruri sunt mai mari. Singurul scor care satisface acest criteriu este 5, deci Q₁ = 5. Cea de-a doua cuartila, mediana, este scorul central, i.e. 12. Cea de-a treia cuartila este valoarea fata de care cel mult 75% din scoruri, i.e. cel mult 11, 25 scoruri sunt mai mici si cel mult 25% din scoruri, i.e. 3,75 scoruri sunt mai mari. Singurul scor care satisface acest criteriu este 21, deci Q₃ = 21.

De notat ca (n/100)25 = n(0,25), iar (n/100)75 = n(0,75). Ca atare, pentru Q₁ putem folosi formula n(0,25), iar pentru Q₃ formula n(0,75) sau, echivalent, n - n(0,25). In exemplul nostru, n(0,25) = 3,75 si n(0,75) = n - n(0,25) = 11,25.

Uneori, percentila cautata "cade" intre doua scoruri din multimea respectiva. Intr-un astfel de caz, prin conventie, se alege media aritmetica a celor doua scoruri pentru a aproxima percentila cautata. Sa presupunem ca ne intereseaza ce-a de-a 20-a percentila din multimea de mai sus. Aceasta ar fi valoarea fata de care cel mult 3 scoruri sunt mai mici si cel mult 12 scoruri sunt mai mari. Intrucat orice numar cuprins intre 4 si 5 (inclusiv) satisface acest criteriu, vom alege 4,50 drept ce-a de-a 20-a percentila.

Procedura de calcul a percentilelor pentru date grupate este asemanatoare procedurii de calcul a medianei pentru date grupate. Sa consideram din nou distributia de frecvente a scorurilor obtinute la un test de cunostinte de 180 de subiecti si sa presupunem ca ne intereseaza cea de-a 75-a percentila. Pentru a o afla, vom folosi tabelul 3.8, care include o coloana de frecvente cumulate.

Mai intai, identificam intervalul de clasa care contine percentila cautata. Avand 180 de scoruri individuale in esantion, P₇₅ este valoarea fata de care cel mult 135 (180 0,75) de scoruri sunt mai mici si cel mult 45 (180 - 135) de scoruri sunt mai mari. Ca atare, intervalul de clasa care contine percentila cautata este cel care contine valoarea fata de care cel mult 135 (180 0,75) de scoruri sunt mai mici. Inspectand coloana de frecvente cumulate din tabelul 3.8, constatam ca 122 de cazuri sau scoruri s-au cumulat sub limita superioara a intervalului 50-54 si ca 159 de cazuri sau scoruri s-au cumulat sub limita superioara a intervalului 55-59. Stim acum ca P₇₅ este o valoare cuprinsa intre limita reala inferioara si limita reala superioara ale intervalului 55-59, adica intre 54,5 si 59,5. Mai departe, presupunem ca toate cele 37 de cazuri situate in acest interval sunt distribuite uniform intre limitele reale ale intervalului, cazul 123 fiind situat la limita reala inferioara (54,5), iar cazul 159 la limita reala superioara (59,5). In intervalul care contine P₇₅ sunt 37 de cazuri, cazul 135 fiind al 13-lea: cazul 123 este primul, 124 al doilea, ., 135 al 13-lea. Aceasta revine la a spune ca, pentru a afla al catelea caz este cazul 135, scadem din 135 frecventa cumulata a cazurilor aflate sub intervalul in care se afla cazul 135: 135 - 122 = 13. Daca, asa cum am presupus, scorurile sunt distribuite uniform, atunci cazul 135 se afla la 13 37 din distanta dintre 54,5 si 59,5. Acum, 13 37 din 5 (marimea intervalului) este 1,75, asa incat putem aproxima P₇₅ la 54,5 + 1,75 sau 56,25.

Formula urmatoare rezuma pasii de calcul al percentilelor pentru date grupate:

Formula 3.5 P_m LCRI_m +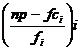

in care LCRI_m = limita de clasa reala inferioara a intervalului care contine P_m

n = numarul total de scoruri

p = proportia corespunzatoare percentilei cautate P_m

fc_i = frecventa cumulata sub intervalul care contine P_m

f_i = numarul de cazuri din intervalul care contine P_m

i = marimea intervalului

Aplicand formula 3.5 la exemplul nostru, avem:

P₇₅ 54,5 + = 54,5 + 1,75 = 56,25

Sa presupunem acum ca ne intereseaza procentul de subiecti care au obtinut un scor mai mic sau egal cu 47 si ca nu dispunem decat de datele grupate din tabelul 3.8. Procentul de cazuri care au un scor mai mic sau egal cu un scor dat se numeste rangul percentilei scorului respectiv.

Pentru a afla rangul percentilei pentru scorul 47, notat RP₄₇, observam mai intai ca acest scor este cuprins in intervalul 45-49 si ca 50 de cazuri s-au cumulat sub limita reala inferioara a acestui interval, 44,5. Ca si pana acum, vom presupune ca toate cele 42 de cazuri situate in acest interval sunt distribuite uniform intre limitele reale ale intervalului. Sub aceasta presupunere, proportia de cazuri din interval care au scoruri mai mici sau egale cu 47 este (47,0 - 44,5)/5 = 2,5/5 = 0,5. Ca atare, in acest interval sunt 42 0,5 = 21 de scoruri mai mici sau egale cu 47. Prin urmare, numarul total de scoruri mai mici sau egale cu 47 este 50 + 21 = 71, iar rangul percentilei scorului 47 poate fi aproximat la (71/180) 100 = 39,4. Aceasta inseamna ca 39,4% din cazuri au un scor mai mic sau egal cu scorul 47.

Urmatoarea formula rezuma pasii de calcul al rangului percentilelor pentru date grupate:

Formula 3.6 RP_X

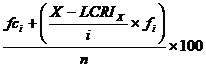
in care fc_i = frecventa cumulata sub intervalul care contine scorul X

X = scorul pentru care se determina RP_X.

LCRI_X = limita de clasa reala inferioara a intervalului care contine scorul X

i = marimea intervalului

f_i = numarul de cazuri din intervalul care contine scorul X

n = numarul total de cazuri

Aplicand aceasta formula la exemplul nostru, avem:

RP₄₇ 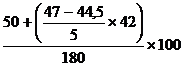= = 39,4

Percentilele si rangul percentilelor pentru date grupate pot fi aproximate si folosind ogivele. Pentru exemplificare, sa folosim ogiva construita in capitolul anterior pentru scorurile celor 180 de subiecti:

Figura 3.4 Ogiva pentru scorurile obtinute

la un test de cunostinte

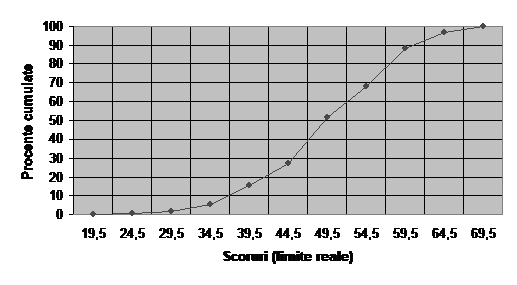
Pentru a afla, de pilda, P₅₈, din punctul 58 de pe axa procentelor trasam o paralela cu axa scorurilor care sa intersecteze curba, iar din punctul de intersectie trasam o perpendiculara pe axa scorurilor. Punctul de intersectie al acestei perpendiculare cu axa scorurilor este P₅₈. Pentru a afla RP₆₂, din punctul 62 de pe axa scorurilor trasam o paralela cu axa procentelor care sa intersecteze curba, iar din punctul de intersectie trasam o perpendiculara pe axa procentelor. Punctul de intersectie al acestei perpendiculare cu axa procentelor este RP₆₂.