Marimi ale corelatiei la nivel ordinal

MARIMI ALE CORELATIEI LA NIVEL ORDINAL

Vom prezenta patru coeficienti ai corelatiei, utilizabili la nivel ordinal: γ al lui Goodman si Kruskal, d al lui Somer, τ_b al lui Kendall si ρ_s al lui Spearman[1]. Acesti coeficienti iau valori cuprinse intre 0 si 1 (τ_b numai pentru cazul r = c).

Coeficientul γ se utilizeaza in situatii de cercetare in care avem doua variabile masurate la nivel ordinal cu un numar mic de valori (nu mai mult de cinci sau sase). Sa presupunem ca am obtinut urmatoarele date privind vechimea in munca si descurajarea profesionala pentru un esantion de 100 de cadre didactice din invatamantul primar:

Tabelul 7 Vechimea in munca si descurajarea profesionala

In cele ce urmeaza, cazurile care fac parte din aceeasi categorie a unei variabile vor fi numite cazuri legate ale variabilei respective.

Pentru a calcula coeficientul γ, sunt necesare doua cantitati, notate cu N_a si respectiv N_d. Cantitatea N_a reprezinta numarul total de perechi de cazuri nelegate si dispuse in aceeasi ordine in privinta ambelor variabile. Cantitatea N_d reprezinta numarul total de perechi de cazuri nelegate si ordonate diferit in privinta celor doua variabile. Pentru aflarea acestor doua cantitati, vom lucra cu frecventele celulelor, considerand celula cu celula.

Pentru inlesnirea referirii la celulele unui tabel n m vom numerota randurile de la 1 la n incepand de sus in jos si, de asemenea, coloanele de la 1 la m incepand de la stanga la dreapta; pentru fiecare celula, vom folosi o notatie de forma c_ij, in care i este numarul randului, iar j numarul coloanei. Pentru un tabel 3 3, cum este 7, avem:

Sa observam ca daca alcatuim perechi selectand un caz dintr-o celula c_ij si un caz dintr-o celula situata pe acelasi rand cu c_ij, obtinem perechi de cazuri legate ale variabilei Y, iar daca alcatuim perechi selectand un caz dintr-o celula c_ij si un caz dintr-o celula situata pe aceeasi coloana cu c_ij, obtinem perechi de cazuri legate ale variabilei X. Evident, daca alcatuim perechi din aceeasi celula, obtinem perechi de cazuri legate in privinta ambelor variabile. Daca, insa, alcatuim perechi selectand un caz dintr-o celula c_ij si un caz dintr-o celula situata deasupra si la dreapta celulei c_ij, cazurile din perechile astfel obtinute sunt nelegate si dispuse in aceeasi ordine in privinta ambelor variabile. De pilda, daca alcatuim o pereche selectand un caz din celula c₃₁ si un caz din celula c₁₂, cazul din celula c₃₁ are o vechime mai mica decat cazul din celula c₁₂ si la fel, cazul din celula c₃₁ are un nivel de descurajare profesionala mai mic decat cazul din celula c₁₂. Numarul total de perechi de cazuri alcatuite selectand un caz din celula c₃₁ si un caz din celula c₁₂ se afla inmultind frecventele din cele doua celule: 20 11 = 220. Cu alte cuvinte, contributia acestor doua celule la cantitatea N_a este de 220 de perechi. Procedand la fel pentru fiecare dintre celelalte trei celule situate deasupra si la dreapta celulei c₃₁ (c₁₃, c₂₂ si c₂₃) si adunand produsele astfel obtinute aflam numarul total de perechi de cazuri alcatuite selectand un caz din celula c₃₁ si un caz din fiecare celula situata deasupra si la dreapta celulei c₃₁:

(20 11) + (20 21) +(20 15) + (20 5) = 1040

Acelasi calcul il putem efectua dupa cum urmeaza:

20(11 + 21 + 15 + 5) = 1040

Prin urmare, pentru a afla cantitatea N_a, se inmulteste frecventa din fiecare celula cu suma frecventelor din toate celulele situate deasupra si la dreapta celulei respective, dupa care se aduna produsele astfel obtinute. De notat ca nici una dintre celulele situate pe primul rand sau pe ultima coloana nu poate contribui la N_a, deoarece nu exista celule situate deasupra si la dreapta acestora. Calcularea N_a pentru tabelul 7 decurge dupa cum urmeaza:

Pentru c₃₁: 20(11 + 21 + 15 +5) = 1040

Pentru c₃₂: 6(21 + 5) = 156

Pentru c₂₁: 10(11 + 21) = 320

Pentru c₂₂: 15 21 = 315

N_a = 1831

Procedeul de calculare a N_d urmeaza o schema simetrica fata de cel pentru N_a, caci daca alcatuim perechi selectand un caz dintr-o celula c_ij si un caz dintr-o celula situata deasupra si la stanga celulei c_ij, cazurile din perechile astfel obtinute sunt nelegate si ordonate diferit in privinta ambelor variabile. De pilda, daca alcatuim o pereche selectand un caz din celula c₃₃ si un caz din celula c₁₁, cazul din celula c₃₃ are o vechime mai mare decat cazul din celula c₁₁ si un nivel de descurajare profesionala mai mic decat cazul din celula c Prin urmare, pentru a afla cantitatea N_d, se inmulteste frecventa din fiecare celula cu suma frecventelor din toate celulele situate deasupra si la stanga celulei respective, dupa care se aduna produsele astfel obtinute. Ca mai sus, sa observam ca nici una dintre celulele situate pe primul rand sau pe prima coloana nu poate contribui la N_d, deoarece nu exista celule situate deasupra si la stanga acestora. Calcularea N_d pentru tabelul 7 decurge dupa cum urmeaza:

Pentru c₃₃: 4(8 + 11 + 10 +15) = 176

Pentru c₃₂: 6(8 + 10) = 108

Pentru c₂₃: 5(8 + 11) = 95

Pentru c₂₂: 15 8 = 120

N_d = 499

In tabelul 7, un numar total de 1831 de perechi de cazuri sunt nelegate si dispuse in aceeasi ordine in privinta ambelor variabile si un numar total de 499 de perechi de cazuri sunt nelegate ordonate diferit in privinta celor doua variabile.

Coeficientul γ se calculeaza cu ajutorul urmatoarei formule:

Formula 6

Valoarea coeficientului γ pentru datele din tabelul 7 este:

Vom conchide ca vechimea in munca este corelata moderat cu nivelul de descurajare profesionala, aceasta corelatie fiind pozitiva: daca, de pilda, stim ca A are o vechime mai mare in munca decat B, suntem indreptatiti sa spunem ca este probabil ca A sa aiba un nivel de descurajare profesionala mai inalt decat B.

Este important de observat ca aplicarea coeficientului γ presupune (pentru a obtine cantitatile N_a si N_d) ca tabelul pe care se lucreaza sa fie construit in maniera tabelului 7, cu categoriile de pe coloane dispuse in ordine crescatoare de la stanga la dreapta si categoriile de pe linii dispuse in ordine crescatoare de jos in sus. γ este o marime simetrica a corelatiei: valoarea acestui coeficient va fi aceeasi indiferent de variabila care este luata ca independenta.

Ca si γ, coeficientii d al lui Somer si τ_b al lui Kendall se utilizeaza in situatii de cercetare in care avem doua variabile masurate la nivel ordinal cu un numar mic de valori si necesita calcularea cantitatilor N_a si N_d. In plus, acesti coeficienti necesita calcularea a doua cantitati, notate L_y si respectiv L_x. Cantitatea L_y reprezinta numarul total de perechi de cazuri legate ale variabilei dependente. Cantitatea L_x reprezinta numarul total de perechi de cazuri legate ale variabilei independente.

Numarul total de perechi de cazuri legate ale variabilei dependente, L_y, se determina afland numarul de perechi de cazuri de pe fiecare rand (prin definitie, toate cazurile aflate pe acelasi rand sunt legate in privinta variabilei dependente) si adunand cantitatile astfel obtinute. Pentru a afla contributia fiecarui rand la L_y, se inmulteste frecventa din fiecare celula cu suma frecventelor din toate celulele situate la dreapta (pe randul respectiv), dupa care e aduna produsele astfel obtinute. Evident, celulele situate pe ultima coloana nu pot contribui la L_y, deoarece nu exista celule situate la dreapta acestora. Calcularea L_y pentru tabelul 7 decurge dupa cum urmeaza:

Pentru randul 1: 8(11 + 21) + (11 21) = 487

Pentru randul 2:10(15 + 5) + (15 5) = 275

Pentru randul 3: 20(6 + 4) + (6 4) = 224

L_y = 986

Numarul total de perechi de cazuri legate ale variabilei independente, L_x, se determina analog, lucrand insa pe coloane. Pentru a afla contributia fiecarei coloane la L_x, se inmulteste frecventa din fiecare celula cu suma frecventelor din toate celulele situate dedesubt (pe coloana respectiva), dupa care e aduna produsele astfel obtinute. Evident celulele situate pe ultimul rand nu pot contribui la L_x, deoarece nu exista celule situate dedesubtul acestora. Calcularea L_x pentru tabelul 7 decurge dupa cum urmeaza:

Pentru coloana 1: 8(10 + 20) + (10 20) = 440

Pentru coloana 2:11(15 + 6) + (15 6) = 321

Pentru coloana 3: 21(5 + 4) + (5 4) = 209

L_x = 970

In tabelul 7 avem un numar total de 986 de perechi de cazuri legate ale variabilei dependente si un numar total de 970 de perechi de cazuri legate ale variabilei independente.

Coeficientul d al lui Somer se calculeaza cu ajutorul urmatoarei formule:

Formula 7

Sa observam ca aceasta formula difera de formula pentru γ numai prin adunarea cantitatii L_y la numitor, ceea ce face ca d sa fie o marime a corelatiei mai conservatoare decat γ, deoarece valoarea lui d va fi intotdeauna mai mica decat valoarea lui γ pentru acelasi tabel. Pentru tabelul 7, avem:

Aceasta valoare a coeficientului d indica o corelatie pozitiva cel mult moderata intre cele doua variabile.

Dupa cum se poate constata, coeficientul d este o marime asimetrica a corelatiei. Daca variabila ale carei categorii sunt capete de randuri este luata drept variabila independenta, atunci se calculeaza numarul de perechi de cazuri pe coloane si nu pe randuri (in notatia noastra, in formula 7 se ia L_x in loc de L_y ). In cazul datelor din tabelului 7, valorile cantitatilor L_x si L_y sunt apropiate, ceea ce inseamna ca o astfel de schimbare nu ar afecta mult valoarea coeficientului d. In cazul in care cele doua cantitati sunt sensibil diferite, trebuie sa fim precauti in privinta alegerii variabilei dependente, deoarece valoarea lui d poate fi considerabil afectata de aceasta decizie.

Coeficientul τ_b al lui Kendall este o marime simetrica a corelatiei, intrucat tine cont atat de L_y, cat si de L_x. Formula sa de calcul este urmatoarea:

Formula 8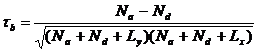

Pentru tabelul 7 avem:

Particularitatea coeficientului τ_b consta din aceea ca poate lua valori cuprinse intre 0 si 1 doar pentru tabele patratice (r = c), deci nu se recomanda calcularea sa pentru orice tabel rectangular.

Coeficientul ρ_s al lui Spearman se utilizeaza, de regula, in situatii de cercetare in care avem doua variabile masurate la nivel ordinal, care au o amplitudine relativ larga de scoruri diferite si putine cazuri legate in privinta fiecarei variabile. Sa presupunem ca dorim sa verificam ipoteza conform careia persoanele care practica jogging au un sentiment mai puternic de respect fata de sine. Pentru aceasta, 10 persoane care practica jogging au fost chestionate cu ajutorul a doua scale, prima masurand gradul de implicare in practicarea jogging-ului, cealalta masurand nivelul respectului fata de sine. Datele obtinute, impreuna cu o serie de calcule cerute de determinarea coeficientului ρ_s, sun prezentate in tabelul 8.

Tabelul 8 Practicarea jogging-ului si respectul fata de sine

Mai intai, atribuim ranguri scorurilor fiecarei valori, incepand cu cel mai mare scor. Apoi, pentru fiecare caz, calculam diferenta dintre rangul scorului in privinta primei variabile (X) si rangul scorurilor in privinta celeilalte variabile (Y) (in tabel, coloana etichetata d). Sa observam ca suma acestor diferente este 0, ceea ce inseamna ca diferentele negative sunt egale cu cele pozitive, acesta fiind intotdeauna cazul. Daca obtinem ∑d 0, atunci am gresit in atribuirea rangurilor sau/si in calcularea diferentelor. Fiecare diferenta astfel obtinuta este apoi ridicata la patrat pentru a elimina semnele minus (in tabel, coloana d²), dupa care se calculeaza suma acestor diferente ridicate la patrat, ∑d².

Formula de calcul a coeficientului ρ_s al lui Spearman este urmatoarea:

Formula 9

in care n este numarul de perechi de ranguri. Aplicand aceasta formula la datele din tabelul 8, obtinem:

Acest rezultat indica o corelatie pozitiva puternica intre cele doua variabile, ceea ce sprijina ipoteza cercetarii.

In anumite situatii de cercetare ne intereseaza sa aflam daca doua variabile sunt corelate la nivelul populatiei de referinta. In cazul variabilelor masurate la nivel nominal, semnificatia statistica a unei corelatii este judecata, de obicei, prin intermediul testului χ². De asemenea, testul χ² poate fi aplicat si in cazul corelatiilor dintre variabile masurate la nivel ordinal. Totusi, acest test evidentiaza doar probabilitatea ca frecventele observate sa se datoreze doar intamplarii si, ca atare, nu reprezinta un test direct al corelatiei[2]. Pentru coeficientii γ si ρ_s au fost elaborate teste de semnificatie specifice, in care ipoteza de nul enunta ca nu exista nici o corelatie la nivelul populatiei, deci ca valorile marimilor respective sunt egale cu 0: γ = 0, respectiv ρ_s = 0. Corespunzator, ipoteza alternativa enunta ca γ 0 sau, respectiv, ca ρ_s 0[3]. Astfel, pentru esantioane cu n > 30, distributia de esantionare pentru γ aproximeaza distributia Z si se foloseste urmatoarea formula pentru calcularea statisticii testului:

Formula 10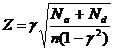

Regulile de decizie sunt cele cunoscute pentru testul Z.

In cazul coeficientului ρ_s, daca 5 n 30, atunci se foloseste tabelul valorilor critice pentru ρ_s (anexa H). Pentru a folosi acest tabel, se identifica valoarea critica a lui ρ_s corespunzatoare numarului de perechi de ranguri, n, si nivelului α ales. Pentru a putea respinge ipoteza de nul si a conchide ca variabilele respective sunt corelate la nivelul populatiei, valoarea obtinuta pentru ρ_s trebuie sa fie mai mare decat valoarea critica. Daca n > 30, atunci distributia de esantionare pentru ρ_s aproximeaza distributia t cu gl = n 2 si se foloseste urmatoarea formula pentru calcularea statisticii testului:

Formula 11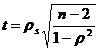

Regulile de decizie sunt cele cunoscute pentru testul t - Student.