Magnetizarea corpurilor

MAGNETIZAREA CORPURILOR.

Miscarii orbitale a electronului, intr‑un corp solid metalic, in jurul nucleului si respectiv momentului cinetic orbital ii corespunde un moment magnetic orbital de­ter­minat de relatia:

(1)

unde: e - este sarcina electronului; m - masa acestuia iar M_co - momentul cinetic or­bi­tal.

De asemenea miscarii spin a electronului, deci momentului cinetic de apin (M_cs) ii corespunde un moment magnetic de spin:

(2)

Dupa relatia (2), rezulta ca momentul magnetic de spin al electro­nu­lui este mai mare decat momentul magnetic orbital (1).

Similar electronului se stabileste momentul magnetic de spin al nucle­ului ato­mic, insa cum masa acestuia este de aproximativ (10³) ori mai mare decat cea a elec­tronului, rezulta tinand seama de (2) ca momentul sau mag­netic de spin este negli­jabil. Daca se ia in considerare faptul ca miscarea orbitala a electronilor este puternic influentata de atomii vecini din reteaua cristalina, rezulta ca orientarea mo­mentelor cinetice orbitale ale electronilor dupa un camp magnetic exterior, este extrem de re­du­sa, incat contributia acestor momente la magnetizarea atomului este neglijabila.

Prin urmare magnetizarea atomului este datorata cu precadere mo­men­telor mag­­netice de spin ale electronilor. Cum starea enegetica a elec­tronului este cuanti­fi­cata si momentele magnetice de spin sunt cunatificate.

Momentul cinetic de spin al electronului conform teoriei cuantice, poa­te avea numai doua directii de orientare in raport cu directia unui camp magnetic exterior si anume:

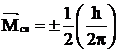(3)

unde: h - este cuanta de energie (adica constanta lui Plank).

Inlocuind (5.03) in (5.02) rezulta ca momentul magnetic de spin al electronului poate avea valorile cunatificate:

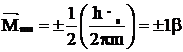(4)

unde valoarea momentului magnetic de spin s‑a considerat drept unitate de masura si se numeste magneton Procopiu-Bohr, dupa numele fizicianului roman Stefan Procopiu (care a stabilit in 1913 momentul magnetic orbital al electronului) si fizi­ci­a­nul N. Bohr. Din (5.04) rezulta ca valoarea unui mag­neton Procopiu-Bohr este 1b = 9,27 · 10^-24 [Am²].

Momentul magnetic propriu al atomului rezulta ca suma cuan­tica a mo­mentelor magnetice ale electronilor si nucleului. In consecinta ele­mentele ale caror electroni isi compenseaza reciproc momentele magnetice de spin, ca si cele orbitale, cum sunt atomii care au straturile electronice com­plet ocupate, prezinta moment mag­netic al atomului nul. Elementele de tranzitie insa, cum sunt Fe, Co si Ni poseda stra­turi electronice incomplete, astfel ca atomii acestora prezinta momente magnetice ale electronilor necom­pensate. Fierul de exemplu, poseda pe stratul (3d) cinci elec­troni de spin pozitiv (+5) si un electron de spin negativ (-1) deci un moment mag­ne­tic propriu avand valoarea (4b). La fel pentru Co exista trei electroni necom­pensati, iar Ni are doi electroni necompensati.

Deci conditia ca un atom sa posede moment magnetic propriu rezida in existenta electronilor cu spini necompensati, in structuri electronice incomplete.

Vectorul de magnetizare al corpului, in functie de marimile microsco­pi­ce (adica specifice microparticulelor din atom) rezulta ca suma a momentelor mag­netice proprii ale atomilor din unitatea de volum.

(5)

La nivelul marimilor macroscopice, starea de magnetizare a unui corp izotrop, omogen si cu temperatura constanta in toata masa sa, lipsit de polarizatie magnetica proprie, cand este indtrodus intr‑un camp magnetic exterior de intensitate este de­terminata in fiecare punct al corpului de vectorul inductie magnetica conform legii de legatura in camp magnetic:

(6)

unde: m₀ = 4p · 10^-7 [H/m] este permeabilitatea magnetica a vidului;

c = 1 in S.I.U. si cu (4p) in sistemele nerationalizate, constituie o constanta de proportionalitate. Pentru corpurile cu polarizatie magnetica temporara liniara vectorul de magnetizatie este de forma:

(7)

unde: c_m - constituie susceptivitatea magnetica a corpului. Inlocuind (7) in (6) pentru (c = 1) rezulta

(8)

sau notand:

(9)

care constituie permeabilitatea magnetica relativa, (8) devine:

(10)

unde: m - este permeabilitatea magnetica absoluta a materialului. Din (07) si (09) se obtine vectorul de magnetizatie sub forma:

(11)

dependent de marimile macroscopice determinabile pe cale experimentala, sau legatura intre acestea si marimile microscopice:

(12)

pentru concentratia (n₀) data a atomilor suma din (12) poate fi determinata, consi­de­rand valoarea medie a proiectiei dupa directia campului magnetic exterior.

Magnetizatia poate avea o componenta temporara care este diferita de zero numai daca (H   0) corespunzator relatiei (7) pentru medii liniare, sau o com­ponenta permanenta diferita de zero si in absenta campului magnetic exteri­or.