Determinarea tensiunilor si a sagetii din placile plane circulare incarcate simetric

Determinarea tensiunilor si a sagetii din placile plane circulare incarcate simetric

1 Placa incastrata pe contur

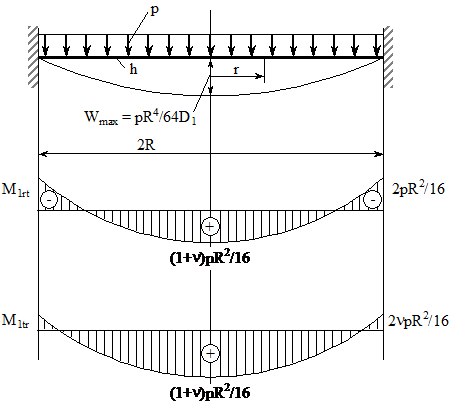
Se considera placa de raza R, grosime h, incastrata pe contur incarcata cu o sarcina uniform distribuita p conform fig. (XVIII.5).

Expresia functiei (XVIII.35) pentru cazul studiat se stabileste in raport de constantele de integrare prin determinarea acestora in baza urmatoarelor conditii:

rotirea in centrul placii (r = 0) este nula, deoarece tangenta la planul deformat este paralela cu planul median al placii nesolicitate:

(XVIII.40)

Relatia poate fi indeplinita daca . Expresia (XVIII.35) capata forma:

(XVIII.41)

din conditia pe contur pusa pentru relatia (XVIII.41) [II.2] pentru , rezulta:

(XVIII.42)

de unde:

(XVIII.43)

Odata stabilite constantele , ale expresiei (XVIII.35) pentru cazul studiat, acestea capata forma:

. (XVIII.44)

Se pot stabili valorile eforturilor moment (XVIII.14), (XVIII.15) avand in vedere ca:

, (XVIII.45)

Fig. XVIII.5 Placa incastrata pe contur

Rezulta:

, (XVIII.46)

. (XVIII.47)

Pentru o placa executata din otel aliat , se obtine:

, (XVIII.48)

. (XVIII.49)

Diagramele momentelor incovoietoare se construiesc conform relatiilor si au o forma parabolica. Se observa ca in centrul placii momentul incovoietor are aceeasi valoare in orice directie, fig. (XVIII.5)

Pentru:

. (XVIII.50)

Pentru:

, (XVIII.51)

. (XVIII.52)

Tensiunile normale maxime corespunzatoare valorilor extreme ale eforturilor in cazul otelului aliat (),(XVIII.37), sunt:

in centrul placii (r = 0)

XVIII.53)

pe contur (r = R)

, (XVIII.54)

. (XVIII.55)

Valoarea cea mai mare a tensiunii este pe contur pe directia razei r, ; in punctele conturului tensiunea minima este pe directia verticala z, unde ; astfel tensiunea echivalenta conform teoriei tensiunilor tangentiale maxime, (XI. 14),  pe contur este :

(XVIII.56)

Fig. XVIII.6 Placa incastrata pe contur

Prin prisma celor prezentate la o solicitare extrema fisurile apar in jurul conturului placii de grosime h pe partea  superioara a acesteia.

XVIII.57)

Din (XVIII.1) se deduce sageata w sub forma (XVIII.39), cunoscand din expresia (XVIII.43) si . Rezulta:

. (XVIII.58)

Pentru determinarea lui se pune conditia:

pentru sageata; rezulta:

, . (XVIII.59)

Expresia sagetii pentru placa circulara incarcata simetric cu o sarcina uniform distribuita, incastrata pe contur este:

. (XVIII.60)

Sageata maxima este pe mijlocul placii (w₀) r =0 si are marimea:

. (XVIII.61)

2 Placa simplu rezemata pe contur

Se considera placa definita in paragraful pecedent numai ca este simplu rezemata pe contur, fig. (XVIII.7). Deoarece si in aceste caz , expresia functiei are forma (XVIII.41).

Conditia pentru determinarea constantei C₁ are in vedere faptul ca pe contur (marginea placii) pentru , (are loc o rotire a marginii placii).

Tensiunea (XVIII.6) se calculeaza prin prisma functiei (XVIII.41) avand in vedere ca:

, (XVIII.62)

. (XVIII.63)

Pentru valoarea cea mai mare a tensiunii pe suprafetele laterale, , rezulta:

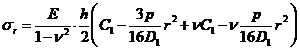XVIII.64)

Pentru , (adica paranteza are valoarea zero) se obtine:

. (XVIII.65)

De unde:

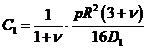. (XVIII.66)

In aceste conditii expresia lui capata forma:

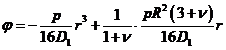. (XVIII.67)

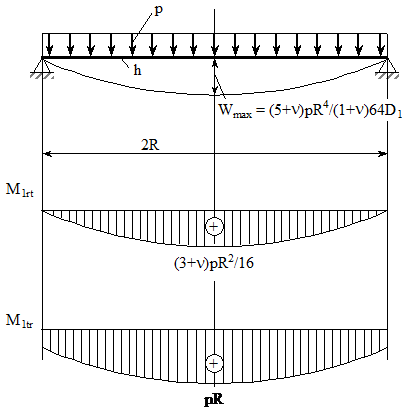
Fig. XVIII.7 Placa simplu rezemata pe contur

Se pot stabili valorile eforturilor moment (XVIII.14), (XVIII.15), avand in vedere ca:

(XVIII.68)

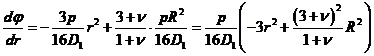. (XVIII.69)

Rezulta:

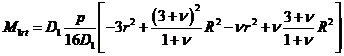, (XVIII.70)

(XVIII.71)

, (XVIII.72)

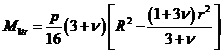. (XVIII.73)

Pentru o placa executata din otel aliat , se obtine:

(XVIII.74)

. (XVIII.75)

Ca si in cazul placii incastrate diagramele momentelor incovoietoare au o forma parabolica, iar in centrul placii momentul incovoietor are aceeasi valoare in orice directie, fig. (XVIII.7).

Din relatiile (XVIII.71), (XVIII.73) se determina valorile momentelor incovoietoare in sectiunile din centrul si marginea placii.

in centrul placii ()

. (XVIII.76)

pe contur ()

, (XVIII.77)

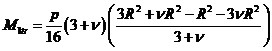, (XVIII.78)

. (XVIII.79)

Tensiunile normale maxime corespunzatoare valorilor extreme ale eforturilor in cazul otelului aliat (),(XVIII.77), sunt:

in centrul placii

. (XVIII.80)

pe contur

, . (XVIII.81)

Tensiunea normala este maxima in centrul suprafetei inferioare a placii si are aceeasi valoare pe oricare directie a razei; tensiunea minima este pe directia z, . Tensiunea echivalenta conform teoriei tensiunilor tangentiale maxime, [XI. 14], in centrul placii este:

. (XVIII.82)

Fisurile apar in centrul suprafetei inferioare a placii, fig. (XVIII.8).

Fig. XVIII.8 Fisuri pe suprafata posterioara

Cunoscand expresia rotirii , (XVIII.67), se determina sageata w, (XVIII.39), cunoscand C₁, (XVIII.66) si C₂=0:

(XVIII.83)

Se pune conditia ca deplasarea w sa fie nula pe contur r = R, w = 0. Rezulta: . De unde:

XVIII.84)

Expresia sagetii este:

(XVIII.85)

Sageata maxima este pe mijlocul placii (w₀) pentru r = 0 si are marimea:

. (XVIII.86)