
|
|
|
DETERMINAREA CONFIGURATIEI MECANISMELOR PLANE
1. Introducere.
Sistemele mecanice care fac parte din mecanica fina, au ca trasatura comuna faptul ca ele stabilesc relatii intre valorile de intrare si iesire, care sunt semnale purtatoare de informatii in aparatele respective.[19];[20];[21];[22].
Mecanismele din domeniul mecanicii fine sunt utilizate cu precadere ca tehnica a transmiterii si prelucrarii semnalelor. [22];[23].
Mecanismele cu elemente rigide, cunoscute in literatura de specialitate si sub denumirea de mecanisme cu parghii, ca parte integranta a sistemelor din mecanica fina, poarta amprenta acestui domeniu, scopul lor functional primordial fiind acela de a transmite si prelucra semnalele mecanice.
Semnalele mecanice pot fi: deplasari, viteze, acceleratii (cinematica), forte si momente (cinetostatica).
Determinarea si cunoasterea pozitiilor tuturor elementelor (sau a unor puncte de pe ele), deci implicit a deplasarilor, este o problema foarte importanta si in determinarea pe mai departe a cunoasterii cinematicii si cinetostaticii mecanismului respectiv.
In acest paragraf vor fi prezentate metodele pentru determinarea pozitiilor tuturor elementelor (a configuratiei) luand in studiu o serie de mecanisme cu articulatii si culise, des intalnite in practica.
Marimile cunoscute apartin urmatoarelor doua categorii:
a) Marimi invariabile: puncte fixe, lungimile (constante) ale elementelor, unghiuri constante;
b) Parametri geometrici conducatori (coordonatele generalizate).
Este cunoscut faptul ca numarul parametrilor conducatori este egal cu gradul de mobilitate M.
Metoda folosita in practica pentru determinarea configuratiei este metoda numerica care este o metoda moderna, cu posibilitatea utilizarii, cu precadere, si a programelor automate de calcul.
Metoda geometrica (grafica) va fi prezentata in acest paragraf doar informativ, pe un singur exemplu de mecanism.
2. Mecanisme cu articulatii.
Exemplul 1.
Metoda grafica.
Fie mecanismul patrulater articulat din fig. 1.32.
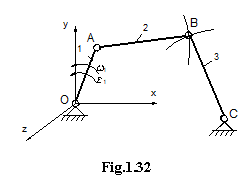 Se cunosc: coordonatele punctelor
fixe O si C, lungimile elementelor
Se cunosc: coordonatele punctelor
fixe O si C, lungimile elementelor ![]() ;
; ![]() ;
;![]() , precum si parametrul
, precum si parametrul ![]() corespunzator
elementului conducator 1. Se duce, intai o dreapta inclinata cu
unghiul
corespunzator
elementului conducator 1. Se duce, intai o dreapta inclinata cu
unghiul ![]() fata de axa X pe care se ia lungimea
fata de axa X pe care se ia lungimea ![]() . Din punctul A
astfel determinat se duce un arc de cerc de raza
. Din punctul A
astfel determinat se duce un arc de cerc de raza ![]() . Analog cu centrul in
C se duce un arc de cerc de
raza
. Analog cu centrul in
C se duce un arc de cerc de
raza ![]() . La intersectia celor doua cercuri se obtine
punctul B.
. La intersectia celor doua cercuri se obtine
punctul B.
Se observa ca aceasta intersectie poate fi:
cu
solutie dubla; in acest caz va trebui indicata solutia care
trebuie considerata (daca nu se face aceasta specificatie
se va alege solutia cea mai apropiata de pozitia
precedenta, in cazul in care intr-o succesiune de valori pentru unghiul ![]() , se considera pasi suficient de apropiati);
, se considera pasi suficient de apropiati);
cu solutie simpla (cele doua cercuri tangente);
fara solutie; in acest caz mecanismul nu poate exista fizic in aceasta pozitie (de exemplu el s-a blocat intr-o pozitie anterioara).[51];[62];[63];[65];[72].
Metoda numerica.
Pentru mecanismul din fig. 1.32 se pot scrie urmatoarele ecuatii:
![]() (1.11)
(1.11)
![]()
Se vor scrie apoi ecuatiile a doua cercuri cu centrul in A si respectiv cu centrul in C:
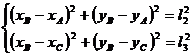 (1.12)
(1.12)
Dupa
gasirea coordonatelor punctului A,
ultimele doua ecuatii (relatiile 1.12) au ca necunoscute ![]() si
si ![]() . Rezolvarea lor se efectueaza prin una din metodele
moderne de calcul.
. Rezolvarea lor se efectueaza prin una din metodele
moderne de calcul.
Exemplul 2.
Metoda analitica (numerica).
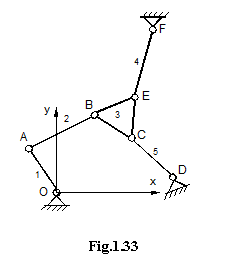 Fie mecanismul din fig. 1.33.,
pentru care se pot scrie ecuatiile:
Fie mecanismul din fig. 1.33.,
pentru care se pot scrie ecuatiile:
![]()
![]() (1.13)
(1.13)
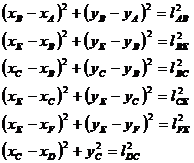 (1.14)
(1.14)
Dupa aflarea coordonatelor punctului A se obtine un sistem de sase ecuatii, avand ca necunoscute cele doua coordonate ale punctelor B, C si E.
Se
observa ca utilizarea metodei Newton pentru calculator nu este
avantajoasa deoarece problema se reduce la aflarea solutiilor unui
sistem de sase ecuatii liniare cu sase necunoscute. Spre
deosebire de aceasta prin metoda gradientului functiei F (![]() ) aflarea necunoscutelor este posibila cu
usurinta.[51];[62];[63];[72].
) aflarea necunoscutelor este posibila cu
usurinta.[51];[62];[63];[72].
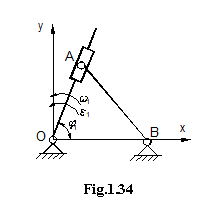
3. Mecanisme cu culise.
Exemplul 3.
Metoda numerica.
Pentru rezolvarea mecanismului din fig. 1.34. se scriu urmatoarele ecuatii:
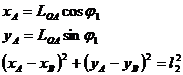 (1.15)
(1.15)
adica trebuie rezolvata o singura ecuatie:
![]() (1.16)
(1.16)
cu necunoscuta ![]() ; se revine la primele ecuatii si se determina
; se revine la primele ecuatii si se determina
![]() si
si ![]() .
.
Exemplul 4.
Metoda numerica.
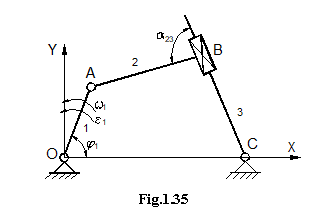
Pentru
rezolvarea mecanismului din fig. 1.35. se scriu succesiv urmatoarele
ecuatii:
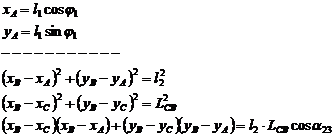 (1.17)
(1.17)
Ultimele
trei ecuatii au ca necunoscute ![]() ,
,![]() ,
,![]() .
.
Produsul scalar care a fost calculat in ultima ecuatie intervine intotdeauna in cazul unghiurilor constante adica in cazul in care nu intervine suprapunerea unei articulatii cu o culisa.