Structura algebrica si topologica a multimilor R si

Modulul 1.1 Multimile R si . Aspecte algebrice.

Pentru a introduce axiomatic multimea R, amintim - pana la definitia 1.5 - cele ce urmeaza.

Definitia 1.1 O multime K, avand cel putin doua elemente, inzestrata cu doua operatii algebrice interne - adunarea, notata cu si inmultirea, notata cu  - astfel incat

( 1.1 )( K,+ ) este grup abelian ( aditiv ),

( 1.2 )( K^*, ) - unde K^* inseamna K , cu 0 elementul neutru in raport cu

- este grup abelian ( multiplicativ ),

( 1.3 )inmultirea este distributiva fata de adunare

se numeste corp comutativ. Acesta se noteaza cu ( K,+, ), iar elementul sau neutru fata de  cu 1.

Observatie. Elementele 0 si 1, precum si simetricele, in raport cu si  , ale oricaror elemente din K sunt unice.

Definitia 1.2 i) O relatie binara pe o multime nevida A, notata cu , se numeste relatie de ordine ( partiala ) pe A daca este reflexiva, antisimetrica si tranzitiva, adica daca sunt satisfacute axiomele:

( r ) x x , x I A ;

( a ) x, y I A , x y si y x T x = y ;

( t ) x, y, z I A , x y si y z T x z .

ii) Multimea A, inzestrata cu relatia de ordine , se numeste ( partial ) ordonata, fiind notata cu ( A,

iii) ( A, ) se numeste total ( liniar ) ordonata cand x, y I A , x y sau x y.

Exemple

1) Multimea ( N, ₁ ) , unde , x, y I N , x ₁ y daca si numai daca exista k I N astfel incat y = x + k, este total ordonata.

2)     ( N, ₂ ) , cu x ₂ y daca si numai daca exista k I N astfel incat y = k x este o multime partial ordonata.

3)     Daca X , iar P(X)= este multimea partilor lui X, atunci relatia de stricta incluziune A B ( x I A T x I B si x^*I B astfel incat x^* A) este una de ordine partiala pe P(X).

4)     Multimea ( Q, ), adica multimea numerelor rationale, dotata cu ordinea uzuala , este total ordonata.

Definitia 1.3 O multime total ordonata ( A, ) se numeste complet ordonata, daca orice submultime nevida si majorata a lui A admite o margine superioara in A.

Observatie. Nu orice multime total ordonata este si complet ordonata.Astfel, de exemplu, ( Q, ) este total ordonata si are submultimea B = nevida si majorata, cu sup Q. Deci B nu are marginea superioara in Q , Q nefiind complet ordonata.

Definitia 1.4 Fie ( K,+, ) un corp comutativ si o relatie de ordine definita pe K.

a) Daca sunt satisfacute axiomele

( O₁ ) ( K, ) este multime total ordonata,

( O₂ ) x, y I K , x y T x + z y + z, z I K,

( O₃ ) x, y I K , x 0, y 0 T x y 0,

K se numeste corp ordonat , fiind notat cu ( K, + ,

b) ( K, + , ) se numeste corp complet ordonat cand multimea ( K, ) este complet ordonata in raport cu relatia de ordine data

Teorema 1.1 Intr-un corp comutativ si ordonat ( K, + , ) sunt adevarate urmatoarele afirmatii:

( 1.4 ) x, y I K are loc una si numai una din relatiile:

x < y ( x y si x y ), x = y, x > y ( x y si x y );

( 1.5 ) 0 < 1;

( 1.6 ) 0 < x T x < 0;

( 1.7 ) x, y, z, t I K, x y si z t T x + z y + t;

( 1.8 ) x, y I K, x 0 si y 0 T x y 0;

( 1.9 ) x, y, z I K, x y si z 0 T x z y z.

Demonstratia se bazeaza pe definitiile 1.1, 1.2 si 1.4

Observatie. ( Q, ) - in raport cu operatiile uzuale de adunare si inmultire  precum si cu ordinea uzuala - este un corp comutativ ordonat, dar necomplet, pentru ca, a I Q , x si y I R astfel incat a < x si y < a

Definitia 1.5 ( a corpului R )a) Un corp comutativ si complet ordonat ( in raport cu operatiile  si cu relatia ) , incluzand pe Q, se numeste multime a numerelor reale sau sistem al numerelor reale si se noteaza cu R.

b) Elementele din R se numesc numere reale , iar ( R, ) este denumit corpul numerelor reale.

Observatie. In mod obisnuit, in R, inversul fata de  al unui element arbitrar x ( 0 se noteaza prin , iar rezultatul inmultirii oricarui element y, cu el insusi, de n ( I N^* s N ) ori, prin yⁿ .

Teorema 1.2 R are urmatoarele proprietati algebrice fundamentale:

( p₁ ) x I R, x > 0, n I N^*, astfel incat x n < x + 1;

( p₂ ) x, y I R, y > 0, n I N astfel incat x n y ( principiul lui Arhimede );

( p₃ ) x I R , x > 0 si n I N , n 2, exista si este unic y I R , y > 0, astfel incat

yⁿ = x ( y se noteaza cu si se numeste radacina reala, de ordin n, a lui x );

( p₄ ) xIR, x > 0, nI N^* astfel incat ;

( p₅ ) x, yIR, x < y, r I Q astfel incat x < r < y .

Demonstratia se poate vedea consultand bibliografia ([10], [11], [13]).

Definitia 1.6 Fie ( R, ) corpul numerelor reale.

a) Aplicatia | |: R R definita prin si verificand axiomele:

( N₁ ) | x | 0, x I R si |x| = 0 x = 0,

( N₂ ) | x y | = | x | | y |, x, yI R,

( N₃ ) | x + y | | x | + | y |, x, y I R

se numeste functie modul ( valoare absoluta sau norma ) pe R.

b) Aplicatia d: R R R, data de , , care satisface axiomele

( D₁ ) d(x, y) 0, x, y I R si d(x, y) = 0 x = y,

( D₂ ) d(x, y) = d(y, x), x, y I R,

( D₃ ) d(x, y) d(x, z) + d(z, y), x, y, z I R

se numeste distanta ( metrica uzuala ) pe R.

Observatie. In R, sunt cunoscute urmatoarele relatii:

( 1.10 ) , x, y I R;

( 1.11 ) 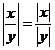, x, y I R, y 0;

( 1.12 ) | x | a a x a x I R si a > 0.

Definitia 1.7 Daca ( K',+, ) si ( K'',+, ) sunt doua corpuri ordonate, atunci o functie f: K^' K^'' , bijectiva si cu proprietatile ( de pastrare a operatiilor si 

f(x + y) = f(x) + f(y), x, yI K^',f(x y) = f(x) f(y), x, y I K^'

si ( de pastrare a relatiei de ordine

x y T f(x) f(y), x, y I K^',

se numeste izomorfism de corpuri ordonate.

Se poate vedea ca un corp complet ordonat este unic pana la un izomorfism de corpuri ordonate. Mai exact, relativ la R, are loc urmatorul rezultat:

Teorema 1.3 ([13]) Corpul complet ordonat al numerelor reale, introdus aici axiomatic ( prin Definitia 1.5), este unic determinat pana la un izomorfism de corpuri complet ordonate.

Observatii.

1.     Exista ([6], [13]) cel putin patru moduri de a defini corpul numerelor reale: constructia lui Dedekind (cu taieturi), constructia lui Cantor (cu siruri Cauchy de numere rationale), constructia zecimala (cu fractii zecimale infinite, neperiodice) si constructia axiomatica.

2.     Modelul geometric pentru R este dat prin stabilirea unei corespondente biunivoce intre punctele unei drepte (numita axa reala) si elementele lui R, folosind conceptul de coordonata pe axa. Din acest motiv, in loc de R, mai spunem dreapta reala sau dreapta numerica reala.

3.     Bijectia intre R si punctele unei drepte permite realizarea unor rationamente de factura geometrica in anumite demonstratii, precum si folosirea unui limbaj geometric in prezentarea unor notiuni si afirmatii din discipline matematice ce fac referire la R.

Exista situatii in care este de descris, in termeni matematici, ce se intampla "dincolo" sau "dincoace" de orice numar real fixat. Altfel spus, avem nevoie de multimea .

Definitia 1.8 Fie doua elemente, notate cu - si + , care nu sunt numere reale si care satisfac axiomele:

- <

A-I)       - < x < xIR

(+ )+x=+ xIR

A-II)

(- )+x=- xIR

A-III)

A-IV) sunt fara sens operatiile (+ ) , 0 ) , .

Multimea , notata cu , pe care se pastreaza adunarea, inmultirea si ordinea de pe R, cu respectarea regulilor uzuale de calcul si a axiomelor A-I ~ A-IV, se numeste multimea extinsa a numerelor reale ( dreapta reala incheiata sau dreapta reala compactificata ).

Observatii

1. Elementele - si + (din ) se numesc minus infinit si respectiv plus infinit( punctele de la infinit ale dreptei reale ). Intrucat, prin axiomele A-II si A-III, - si + au o parte din proprietatile de calcul ale numerelor reale, ele se considera numere improprii.

2. Adunarea si inmultirea nu sunt operatii (algebrice, interne) peste tot definite pe si, din acest motiv, nu dau o structura algebrica pe .

3.Prin extinderea relatiei de ordine de la R la ( prin axioma A-I ), ( , ) este o multime total ordonata.

Modulul 1.2-Aspecte topologice ale lui R si

Definitia 1.9 O submultime I R se numeste interval daca are proprietatea:

( 1.13 ) a, b I I si c I R, a c b T c I I.

Observatii.

1.     Multimile R si sunt intervale.

2.     a, b I R, a < b, sunt intervale multimile:

(a, b) [a, b] = ,

(a, b] = ,                    [a, b) = ,

(a, + [a, +

, b) = ,                        (- , b] = .

In acest sens, R = (- ) si = (a, a), a I R.

3.     Interval in inseamna o multime I de forma (a, b), [a, b], (a, b] sau [a, b), unde a, b I si a < b. Astfel, .

4.     Daca I este interval din , atunci J I R este un interval din R.

In R, are loc urmatorul rezultat:

Teorema 1.4 (Cantor - Dedekind) ([16]) Daca este o familie de intervale inchise si marginite din R, I_n = [a_n, b_n], n I N, astfel incat I_n I_n+1, nIN, atunci este o multime nevida. Aceasta multime este unipunctuala cand ( adica ) tinde la 0 cand .

Definitia 1.10Fie R si din .

1)     Se numeste vecinatate a elementului x₀ o submultime V R pentru care exista un interval deschis (a, b) R astfel incat x₀ I (a, b) V.

2)     Se numeste vecinatate a elementului + o submultime W pentru care exista aIR astfel incat (a, + W.

3)     Se numeste vecinatate a elementului - , o submultime W pentru care exista aIR astfel incat [- , a) W.

Se noteaza cu V(x₀) ( P(R)) sistemul tuturor vecinatatilor lui x₀ I R, cu V(+ ) sistemul tuturor vecinatatilor elementului + si cu V(- ) sistemul tuturor vecinatatilor elementului - . Este evident ca V(x) , , deoarece V(x).

Teorema 1.5 xI, multimea V(x) are urmatoarele proprietati care o caracterizeaza:

( v₁ ) VI V(x), x I V ( V VI V(x) );

( v₂ ) VI V(x), W , V W T W I V(x);

( v₃ ) V, W I V (x) T V W I V (x)

( v₄ ) VI V (x), UI V (x) , astfel incat yIU T VI V (y).

Demonstratie. ( v1 ) VI V (x) T (a, b) astfel incat x I(a, b) V(x). Deci xIVsi V

( v2 ) VI V (x) ,W , cu V W (a, b) , astfel incat xI(a, b) V W. Deci x I(a, b) W, adica W I V (x).

( v3 ) V, W I V (x) , (a, b) , astfel incat xI(a, b) Vsi (c, d) , astfel incat xI(c, d) W. Luand a = max si b = min, avem xI a b V W. DeciV W I V (x).

( v4 ) VI V (x), (a, b) , astfel incat xI(a, b) V. Luand U (a, b), avem: yIU, VI V (y)).◄

Teorema 1.6 ( Hausdorff ) x, y I , x y, VI V (x) ,WI V (y), incat V W =

Demonstratie. x y T a = d(x, y) > 0. Luam V= ( x - , x +), W = ( y - , y + ) si atunci V W .◄

Definitia 1.11Fie A o submultime nevida a lui R.

1. Un element x₀IA se numeste punct interior al lui A daca exista VI V (x₀) astfel incat V A.

2. Multimea punctelor interioare ale lui A, notata cu sau cu Int(A), se numeste interiorul lui A.

3. x₀IR se numeste punct de acumulare al lui A, daca

( 1.14 ) VI V (x₀) , ( A - ) V

4. Multimea punctelor de acumulare ale lui A, notata cu A , se numeste multimea

derivata a lui A

5. Un element x₀ I R se numeste punct aderent al multimii A daca

( 1.15 ) VI V (x₀) , A V

6. Multimea punctelor aderente ale lui A, notata cu , este numita aderenta

( inchiderea ) lui A

Observatii.

1.     Evident, au loc incluziunile: A, A'   siA .

2.     Multimea A = are pe 0 ca singur punct de acumulare. Deci, in acest

caz, A'

3.     Pentru A = (a, b) R, avem A' = [a, b] = , caci orice x₀I(a, b) este punct de

acumulare al lui A si, de asemenea, a si b sunt puncte de acumulare pentru A.

4.     Multimea A = N R nu are puncte de acumulare apartinand lui R. Elementul

+ este singurul sau punct de acumulare, din . Deci N' = .

Teorema 1.7 (Bolzano - Weierstrass) ([13], [16])Orice multime infinita si marginita din R admite cel putin un punct de acumulare.

Definitia 1.12

1.     O multime F R se numeste inchisa daca orice punct de acumulare pentru F apartine lui F, adica F' F. Altfel spus, F = .

2.     O multime D R se numeste deschisa daca complementara sa in R, adica R D, este o multime inchisa din R.

Se poate vedea ([13]) ca D este o multime deschisa daca si numai daca D = .

Notam cu F familia multimilor inchise din R si cu T familia tuturor multimilor deschise din R. Evident, F P(R) si T P(R).

Teorema 1.8 ([3], [10], [13])

( i ) F are urmatoarele proprietati caracteristice:

( i₁ ) I F , R I F ;

( i₂ ) F₁, , F_n I F T F = I F ;

( i₃ ) _aII cu F_a I F, aI I T F = I F .

( ii ) T are proprietatile :

( ii₁ ) I T , R I T ;

( ii₂ ) _aII cu D_a I T, aI I T D = I T ;

( ii₃ ) D₁, , D_n I T T D = I T ,

unde I este o multime de indici.

Observatii.

1. T se numeste topologie ( uzuala ) pe R.

2. D I T , D si xID T DIV(x).

3. Orice D I T se poate reprezenta printr-o reuniune oarecare de intervale deschise din R, adica D = , unde a_a, b_a I R si a_a < b_a a II

4. a, b I R, cu a b T [a, b] I F. De asemenea, si apartin lui F . Orice submultime finita a lui R este din F. Q F.

5. (a, b) R, cu a < b T (a, b)I T . La fel, si sunt intervale deschise, ca multimi din T .

Definitia 1.13 i) O multime A R se numeste marginita, daca exista un interval I, marginit, din R, I = , astfel incat A I.

ii)       O multime A R care este marginita si inchisa se numeste multime compacta.

iii)O multime A R este denumita densa in R, daca = R.

Pentru orice a, b R, cu a < b, intervalele , , si sunt multimi marginite in R, iar intervalele , , si sunt nemarginite.

Teorema 1.9 ([13], [16])Multimea Q este densa in R.

Definitia 1.14O multime nevida A R se numeste convexa, daca , x, y I A, l I [0, 1], avem: (1 - l)x + ly I A.

Observatii.

1.     Corespondenta l I R (1 - l)a + lb cu a, b I R este o functie strict crescatoare si surjectiva care aplica intervalul (0, 1) pe (a, b) si respectiv [0, 1] pe [a, b].

2.     In R, este adevarata afirmatia:

( 1.16 ) A este interval A este convexa x, y I A, x < y, [x, y] A.

3.     In , raman valabile teoremele 1.6 si 1.7.

4.     Pentru A R, avem + I A' daca si numai daca A este multime nemarginita in R. In aceste circumstante, teorema 1.7 ( Boltzano - Weierstrass ) are urmatorul enunt:

" In , orice multime infinita are cel putin un punct de acumulare in "

Definitia 1.15 O multime A R se numeste conexa daca nu exista doua multimi (deschise) D₁, D₂ I T, nevide ( D₁ , D₂ ) si disjuncte ( D₁ D₂ = ),astfel incat:

A D₁ D₂, si .

Observatie. Singurele multimi conexe din R sunt intervalele ( de orice tip ).