Dezvoltari ale teoriei lui Markowitz: modelul Sharpe

La 10 ani de la aparitia celebrului articol al lui Markowitz, un tanar student pe nume Bill Sharpe l-a abordat pe Markowitz, care atunci se ocupa de programare liniara la Institutul RAND. Sharpe avea nevoie de materiale pentru o dizertatie si unul din profesorii sai de la UCLA i-a sugerat sa se adreseze lui Markowitz. Markowitz i-a povestit lui Sharpe despre munca sa de cercetare, legata de teoria portofoliului si de necesitatea calcularii  nenumaratelor covariante. Sharpe l-a ascultat extrem de atent si apoi s-a intors la UCLA.

Anul viitor, in 1963, a fost publicata disertatia lui Sharpe, cu titlul Un model simplificat al analizei de portofoliu . Avand ca baza de pornire ideile lui Markowitz, Sharpe a sugerat o metoda matematica mai simpla  care ar fi evitat nenumaratele calcule ale covariatelor, specifice modelului Markowitz.

Sharpe a afirmat ca toate titlurile de valoare se afla in legatura cu un anumit factor de baza. Acest factor poate fi indicele bursei, produsul national brut, sau un alt indice de pret, atat timp cat are o influenta importanta asupra evolutiei pretului titlului financiar. Utilizand teoria lui Sharpe, un analist va trebui doar sa masoare legatura dintre titlul de valoare si factorul de baza dominant. Se simplifica astfel foarte mult abordarea matematica a lui Markowitz.

Sa analizam putin actiunile comune. Conform teoriei lui Sharpe, factorul de baza pentru pretul actiunilor - singurul care influenteaza major comportamentul lor - ar fi piata actiunilor insasi. ( La fel de important, dar cu mai mica influenta ar fi si ramura  industriala, precum si caracteristicile specifice ale actiunii insasi). Daca pretul actiunii este mai volatil decat piata privita ca intreg, detinerea actiunii va face ca portofoliul sa fie mai variabil si mai riscant. Altfel, daca pretul actiunii este mai putin volatil decat piata, detinerea actiunii va face ca portofoliul sa fie mai putin variabil, mai putin riscant. Deci, variatia (volatilitatea) portofoliului poate fi simplu determinata prin cuantificarea variatiei medii a titlurilor de valoare individuale ce formeaza portofoliul.

Numele dat de Sharpe unitatii de masura a volatilitatii (variatiei)  este factorul beta. Beta este definit ca fiind gradul de corelatie intre miscarile de pret ale pietei si cele ale titlului de valoare individual. Actiunile care scad sau cresc in valoare direct proportional cu piata li se atribuie un factor beta egal cu 1. Daca actiunile cresc sau scad in valoare de doua ori mai rapid decat piata, atunci factorul lor beta este egal cu 2; daca modificarile de pret ale actiunilor reprezinta doar 80% din modificarea pietei, atunci factorul lor beta este egal cu 0,8. Bazandu-ne doar pe aceste informatii, putem sa cuantificam valoarea medie a coeficientului beta al portofoliului. Concluzia este ca orice portofoliu cu un beta mai mare de 1 va fi mai riscant decat piata si orice portofoliu cu un beta mai mic decat 1 va fi mai putin riscant.

La un an de la publicarea dizertatiei sale referitoare la teoria portofoliului, Sharpe a prezentat un concept revolutionar, Modelul de evaluare a activelor de capital (CAPM). Acest concept a reprezentat o continuare a modelului sau unifactorial referitor la alcatuirea unor portofolii eficiente.

Conform CAPM, actiunile sunt purtatoare a doua tipuri distincte de risc. Primul tip de risc este acela de a fi pe piata, pe care Sharpe l-a numit risc sistemic. Riscul sistemic este beta si el nu poate fi diversificat. Al doilea tip de risc, numit risc nesistemic, este riscul specific pozitiei economice a companiei. Spre deosebire de riscul sistemic, riscul nesistemic poate fi diversificat prin simpla achizitie a mai multor tipuri de actiuni.

Peter Berstein, cunoscutul scriitor, cercetator si fondator al publicatiei Revista managementului de portofoliu, a petrecut mult timp cu Sharpe si a studiat munca acestuia in detaliu. Bernstein crede ca cercetarile lui Sharpe se indreapta catre o singura concluzie: "Cel mai eficient portofoliu este chiar piata insasi. Nici un alt portofoliu cu acelasi grad de risc nu poate sa-ti ofere un castig mai mare; nici un alt portofoliu care ofera acelasi castig nu poate fi mai putin riscant." Cu alte cuvinte, "Modelul de evaluare al activelor de capital" ne arata ca portofoliul de piata se imbina perfect cu teoria lui Markowitz privind frontiera de eficient.

Simplificarea modelului Markowitz

In vederea definirii multimii de portofolii eficiente descrisa de Markowitz, pentru fiecare titlu financiar trebuie cunoscute castigul prognozat, dispersia, covarianta cu fiecare titlu financiar ce compune portofoliu. Daca multimea eficienta ar trebuie selectata pe baza a 1000 titluri financiare, volumul input-urilor necesare si costurile de prelucrare a informatiilor ar fi intolerabil de exagerate (1000 de castiguri prognozate, 1000 de dispersii, 499500 covariante).

In acest context, nu este realist sa presupunem ca un analist financiar va putea furniza un astfel de volum de input-uri. In ipoteza ca 20 de analisti ar fi responsabili pentru investigarea caracteristicilor relevante a 1000 de titluri, fiecare analist ar trebui sa calculeze aproximativ 25000 de covariante. Volumul de munca ar fi intolerabil si, mai mult, ar fi extrem de dificil sa se aprecieze semnificatia covariantei.

Datorita acestei dificultati practice, modelul lui Markowitz a fost utilizat exclusiv in mediul academic, gasindu-si aplicabilitatea practica in urma simplificarii propuse de catre William Sharpe. Intrucat marea majoritate a titlurilor financiare sunt corelate semnificativ cu piata de capital in ansamblul sau, Sharpe a apreciat ca o simplificare satisfacatoare ar consta in ignorarea covariantelor pentru fiecare titlu financiar si in substituirea acestor informatii cu relatiile existente intre fiecare titlu si piata. Potrivit acestuia, castigul pentru fiecare valoare mobiliara poate fi reprezentat de urmatoarea ecuatie:

unde Ri este castigul titlului i, a_i si b_i sunt parametri, c_i este o variabila aleatoare a carei valoare prognozata este zero, I nivelul anumitor indici, de regula indici de bursa. Cu alte cuvinte, castigul oricarui titlu depinde de o anumita constanta (a) plus valoarea unui indice de bursa (de exemplu, S&P 500) multiplicata cu un anumit coeficient (b) plus o componenta aleatoare. Simplificarea propusa de Sharpe reduce numarul estimarilor pe care analistul trebuie sa le realizeze de la 501500 la 3002 pentru o multime de 1000 titluri financiare.

Simplificarea propusa de Sharpe necesita 3N+2 estimari.

Eforturile de simplificare au fost continuate si de alti teoreticieni. Cohen si Poague au considerat utila recurgerea la mai multi indici decat la unul singur, castigul fiecarui titlu fiind conexat cu indicele cel mai adecvat pentru acel titlu - anumiti indici de productie care intra in componenta Indicelui Agregat al Productiei Industriale calculat de board-ul bancii centrale americane (Federal Reserve). Pe baza rezultatelor empirice rezulta ca utilizarea simplificarilor implica costuri reduse. Astfel, portofoliile care sunt eficiente in urma procesului de simplificare sunt aproape similare portofoliilor eficiente din analiza complexa realizata de Markowitz. Mai mult, daca rezultatele sunt evaluate in termenii celor doua caracteristici relevante ale portofoliilor (castigul prognozat si riscul), portofoliile eficiente din analiza simplificata sunt intr-o mica masura inferioare portofoliilor eficiente din analiza complexa.

Teoria lui Sharpe[1], potrivit careia castigul unui titlu fluctueaza in functie de sensibilitatea acestuia la evolutiile pietei (calculat prin intermediul lui b), implica notiunea de pret al titlurilor (activelor) si relatiile dintre acest pret si sensibilitate. Aceste idei au fost elaborate de Sharpe in celebrul sau articol privind pretul riscului, care va fi abordat in cele ce urmeaza.

Determinarea preturilor activelor financiare

In articolul sau "Preturile activelor financiare capitale: o teorie a echilibrului pietei in conditii de risc", Sharpe a investigat relatiile dintre teoria portofoliului si determinarea preturilor activelor (titlurilor) financiare. Pe de o parte, teoria portofoliului are un caracter normativ prin aceea ca ofera informatii privind modalitatile in care investitorii ar trebui sa se comporte. Insa, teoria portofoliului nu descrie maniera de ajustare a preturilor activelor (titlurilor) individuale pentru a reflecta diferentierile existente in privinta riscului. Pe de alta parte, teoria pietei de capital are un caracter pozitiv, ilustrand relatiile de piata care vor rezulta in conditii de echilibru in cazul in care investitorii urmeaza ideile centrale ale teoriei portofoliului. Aceste relatii sunt repere pentru cuantificarea precisa a riscului portofoliului si a titlurilor individuale.

Ipotezele simplificatoare propuse de Sharpe sunt urmatoarele: aversiunea fata de risc; investitorii au acelasi orizont de timp (o luna, un an) si au estimari omogene cu privire la veniturile viitoare pentru fiecare titlu financiar intr-un orizont de timp dat; rate identice pentru sumele luate si date cu imprumut; costurile tranzactiilor sunt nule, nu se platesc taxe; investitorii sunt rationali in sensul ca doresc detinerea de portofolii eficiente potrivit teoriei lui Markowitz (maximizeaza castigurile prognozate la un anumit nivel al riscului sau, in mod alternativ sau echivalent, minimizeaza riscul la un nivel dat al castigului prognozat). La prima vedere, ipotezele (supozitiile) modelului lui Sharpe pentru determinarea preturilor titlurilor par a fi extrem de restrictive sau chiar absurde astfel incat se poate deduce ca modelul este lipsit de relevanta. Insa, modelul este util cel putin pentru intelegerea anumitor factori care afecteaza preturile titlurilor, nerealismul ipotezelor vor avea cel mult prea putina semnificatie practica decat majoritatea persoanelor ar crede intr-o prima instanta. Dupa abordarea modelului, se vor analiza detaliat aceste ipoteze.

a)     Dreapta pietei de capital

Dreapta pietei de capital descrisa de Sharpe coreleaza castigul prognozat al unui portofoliu eficient cu rata dobanzii pentru titlul cu risc zero si castigul prognozat al pietei:

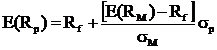
unde E(Rp) castigul prognozat al portofoliului

Rf castigul prognozat al titlului cu risc zero

E(R_M) castigul prognozat al pietei (indice)

 abaterea standard a portofoliului

 abaterea standard a pietei

Intrucat aceasta relatie nu este valabila decat pentru portofoliile eficiente, nu poate fi utilizata pentru descrierea interdependentelor dintre castigurile titlurilor individuale (sau portofoliilor ineficiente) si abaterile lor standard.

b) Castigul prognozat

Potrivit modelului de preturi al activelor (titlurilor) financiare capitale al lui Sharpe, castigul prognozat al oricarui titlu (sau portofoliu) depinde de castigul prognozat al titlului fara risc si de castigul prognozat al intregii piete. Astfel:

unde E(Ri) castigul prognozat al titlului (portofoliului); Rf castigul prognozat al titlului cu risc zero; E(R_M) castigul prognozat al pietei; (coeficientul b) o masura a senzitivitatii (volatilitatii) castigului prognozat al unui titlu la evolutiile pietei.

Aceasta ecuatie este asemanatoare cu dreapta pietei de capital. Intre cele doua relatii de calcul nu exista egalitate, dreapta pietei de capital fiind valabila numai pentru portofoliile eficiente. Riscul este cuantificat prin coeficientul b care inlocuieste abaterea standard. In cazul portofoliilor eficiente, cele doua relatii sunt echivalente. Prin definitie, riscul portofoliilor eficiente este determinat exclusiv de evolutiile pietei, iar castigurile lor prognozate sunt in dependenta liniara cu abaterea standard si coeficientul b

Modelul de preturi al titlurilor (activelor) financiare capitale si implicit ecuatia corespunzatoare sunt reprezentate grafic in figura III.12.

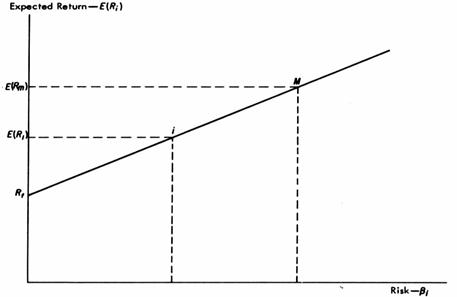
Daca castigul prognozat al titlului fara risc este de 4%, castigul prognozat al pietei este de 10%, coeficientul b este 0,5, castigul prognozat al titlului i este:

E(Ri)=0,04+0,5(0,10-0,04)=0,04+0,5*0,06=0,07

Prima de risc pentru titlul i este egala cu prima de risc a pietei multiplicata cu bi (coeficientul sau b). In acest exemplu, bi=0,5, prima de risc a titlului i este de 0,03, castigul total este egal cu aceasta prima plus castigul prognozat al titlului fara risc sau 0,07.

Ecuatia si graficul anterioare opereaza cu castigul prognozat al unui titlu. Relatia dintre prima de risc efectiva a unui titlu (castigul efectiv minus castigul prognozat al titlului fara risc) si castigul pietei este data de ecuatia de regresie care rezulta pe baza ecuatiei ce utilizeaza prognoze:

Ri castigul efectiv al titlului i, Rf castigul prognozat al titlului fara risc; a_i este o constanta, b_i reprezinta senzitivitatea titlului i fata de piata, R_M castigul pietei, c_i reflecta variatia lui Ri care nu este corelata variatiilor lui R_M . Daca castigurile efective sunt identice cu cele prognozate, valorile lui a_i si c_i vor fi egale cu zero, iar R_i ar fi explicat in totalitate prin intermediul lui R_M , R_f si b_i . Chiar daca perturbatiile intamplatoare ar cauza abateri de la prognoze in orice perioada individuala, in medie a_i si c_i ar fi egale cu zero.

Modelul lui Sharpe prezinta o imagine simpla si totodata interesanta a pietelor financiare. Toti investitorii detin portofolii eficiente care cunosc o evolutie similara cu cea a pietei. Portofoliile difera numai in ceea ce priveste senzitivitatea (volatilitatea) la piata. Preturile tuturor titlurilor riscante se ajusteaza astfel incat, potrivit modelului, castigurile lor sa fie corelate riscurilor pe care le incumba. Aceste riscuri sunt cuantificate cu ajutorul unui indicator statistic simplu (coeficientul b), care indica volatilitatea titlului la evolutiile pietei.

In cazul unui dezechilibru temporar manifestat prin cresterea exagerata a pretului unui titlu ce atrage diminuarea castigurilor prognozate, investitorii vor proceda la vanzarea titlului iar pretul acestuia va reveni la nivelul de echilibru. Desigur si reciproca este valabila (titluri ale caror preturi sunt extrem de scazute si in consecinta vor inregistra castiguri prognozate foarte mari).