Reprezentarea datelor in sistemele de calcul

1. Reprezentari numerice

Am vazut anterior ca numerele sunt reprezentate in calculator sub forma unor siruri de biti (corespunzatori unor cifre in baza 2). In cele ce urmeaza vom prezenta in detaliu modurile de reprezentare a informatiei folosite in sistemele de calcul.

1.2. Scrierea pozitionala

Scrierea pozitionala a reprezentat la aparitia sa un mare pas inainte in matematica. Ca o exemplificare a acestei afirmatii, putem considera adunarea a doua numere naturale oarecare. Daca numerele sunt reprezentate in scriere romana (care nu este pozitionala), se observa imediat ca operatia este foarte dificil de realizat. In schimb, adunarea acelorasi numere reprezentate in baza 10 (care este o scriere pozitionala) este banala. Acest exemplu simplu arata marele avantaj al scrierii pozitionale, si anume ca permite descrierea algoritmica a operatiilor aritmetice, ceea ce o face indispensabila pentru sistemele de calcul.

Un concept fundamental in scrierea pozitionala il constituie baza de numeratie. Spunem ca lucram in baza de numeratie d, care este un numar natural supraunitar, daca avem la dispozitie d simboluri (cifre), avand asociate respectiv valorile 0, 1, , d-1. Un numar este reprezentat intr-o baza oarecare d ca un sir de cifre, fiecare pozitie i din sir avand atasat un factor implicit egal cu dⁱ. Concret, un numar natural N va avea ca reprezentare in baza d sirul de cifre a_n-1a_n-2a₁a₀, a_iI, , cu proprietatea ca . Se demonstreaza ca fiecare numar are o reprezentare unica pentru o baza de numeratie data.

Sa luam ca exemplu numarul 309. (De fapt, corect ar fi fost sa spunem 'numarul care are reprezentarea 309 in baza 10', deoarece si atunci cand scriem un numar, de fapt folosim o reprezentare a s Cum insa un numar este o abstractiune, iar reprezentarea in baza 10 este cea folosita dintotdeauna de oameni pentru a desemna numerele, vom folosi in continuare aceeasi conventie). Reprezentarea sa in baza 10 este evidenta, deoarece 309 = 3 10² + 0 10¹ + 9 10⁰. Sa consideram acum reprezentarea aceluiasi numar in baza 2. Deoarece 309 = 1 2⁸ + 0 2⁷ + 0 2⁶ + 1 2⁵ + 1 2⁴ + 0 2³ + 1 2² + 0 2¹ + 1 2⁰, reprezentarea sa in baza 2 este 100110101. Pentru a specifica baza de numeratie in care este scrisa o reprezentare, se foloseste o notatie ca in exemplul de mai jos:

309₍₁₀₎ = 100110101₍₂₎

Deoarece baza 2 este folosita de calculatoare, iar baza 10 este preferata de oameni, conversia (in ambele sensuri) intre aceste doua baze este adesea necesara. O reprezentare in baza 2 este usor de convertit in baza 10, pur si simplu prin aplicarea formulei , unde a_i sunt bitii care formeaza reprezentarea in baza 2. De exemplu, 1101001₍₂₎ = 1 2⁶ + 1 2⁵ + 0 2⁴ + 1 2³ + 0 2² + 0 2¹ + 1 2⁰ = 105₍₁₀₎. Mai dificila este conversia in sens invers, care se realizeaza dupa urmatorul algoritm:

Se imparte numarul la 2 si se retine restul. Catul se imparte la randul sau la 2, iar procesul de repeta pana cand se obtine catul 0. Reprezentarea in baza 2 este sirul resturilor obtinute, luate in ordine inversa.

Pentru exemplificare consideram din nou numarul 309. Aplicand algoritmul de mai sus, avem (pe coloana din dreapta se gaseste sirul resturilor):

Daca se inverseaza sirul resturilor se obtine 100110101, adica exact reprezentarea calculata mai sus.

Sa consideram acum cazul concret al utilizarii scrierii pozitionale in sistemele de calcul. Reamintim ca intr-un calculator operanzii au dimensiuni standardizate, mai precis octeti sau multipli de octet. O consecinta imediata este finitudinea reprezentarii; cu alte cuvinte, nu putem reprezenta in calculator numere oricat de mari, deoarece numarul de biti disponibil pentru reprezentari este finit. In aceste conditii, este important sa determinam domeniul reprezentabil cu ajutorul operanzilor disponibili, altfel spus, intervalul in care se inscriu numerele cu care putem lucr In mod evident, numarul minim reprezentabil este intotdeauna 0, indiferent de dimensiunea operanzilor. De asemenea, domeniul numerelor reprezentabile nu prezinta 'goluri', ci formeaza un interval: fiind date doua numere naturale x si y care pot fi reprezentate, orice numar natural aflat intre x si y va putea fi la randul sau reprezentat. Mai ramane deci sa determinam valoarea maxima a domeniului, valoarea care depinde de numarul de biti alocat unei reprezentari.

Pentru operanzi de 8 biti, valoarea maxima care poate fi reprezentata este 1 2⁷ + 1 2⁶ + 1 2⁵ + 1 2⁴ + 1 2³ + 1 2² + 1 2¹ + 1 2⁰ = 255. Mai general, daca operanzii au n biti, valoarea maxima care poate fi reprezentata este 1 2^n-1 + 1 2^n-2 + + 1 2¹ + 1 2⁰ = 2ⁿ-1. Domeniul reprezentabil pe n biti, folosind scrierea pozitionala, este deci 0 2ⁿ-1. Revenind la exemplul de mai sus, observamca numarul 309 nu poate fi reprezentat pe 8 biti, in timp ce pe 16 biti are reprezentarea 00000001 00110101 (valorile de 0 de la stanga fiind, bineinteles, nesemnificative).

1.3. Reprezentari cu semn

Scrierea pozitionala nu rezolva toate problemele legate de reprezentarea numerelor in calculator. De exemplu, daca dorim sa lucram cu numere intregi, deci cu semn, scrierea pozitionala singura nu mai este suficienta. Motivul este foarte simplu: in acest caz, pe langa cifrele bazei de numeratie mai este nevoie si de un simbol suplimentar (semnul); deoarece bitii nu au decat doua valori posibile, asociate cifrelor bazei 2, nu avem la dispozitie nici un alt simbol.

Este deci necesar sa se defineasca o noua reprezentare care, folosind in continuare siruri de biti, sa permita lucrul cu numere cu semn. In acelasi timp, dorim sa pastram avantajele scrierii pozitionale, motiv pentru care vom incerca sa derivam noua reprezentare din scrierea pozitionala.

In primul rand, deoarece nu avem la dispozitie un simbol suplimentar, pentru reprezentarea semnului va fi folosit unul dintre biti, care nu va mai avea semnificatia obisnuita unei cifre din scrierea pozitionala. Concret, bitul cel mai semnificativ (cel cu indicele n-1) va indica semnul numarului si va fi numit bit de semn. Prin conventie, valoarea 1 a bitului de semn indica un numar negativ, iar valoarea 0 un numar pozitiv. Desigur, s-ar fi putut alege si conventia inversa; motivul pentru care se prefera forma aleasa are insa avantajul ca, in cazul numerelor pozitive, reprezentarea este aceeasi ca in cazul scrierii pozitionale (bitul de semn fiind in acest caz un 0 nesemnificativ).

Cea mai naturala idee pentru reprezentarea numerelor cu semn este ca bitul cel mai semnificativ sa indice exclusiv semnul, iar ceilalti biti sa reprezinte modulul numarului in scriere pozitionala. Formal, reprezentarea unui numar intreg N este sirul de biti a_n-1a_n-2a₁a₀, cu proprietatea ca .

Desi intuitiva, varianta de mai sus, numita reprezentare modul-semn, are unele dezavantaje. Pe de o parte, reprezentarea modul-semn a unui numar este unica, dar cu exceptia numarului 0: se observa imediat ca in acest caz, daca bitii care formeaza modulul au toti valoarea 0, in schimb bitul de semn poate fi atat 0, cat si 1. Desigur, aceasta redundanta poate crea proleme, in special la compararea numerelor.

Mai important, adunarea numerelor reprezentate cu modul si semn nu mai urmeaza algoritmul clasic, specific scrierii pozitionale. Daca pentru numere cu acelasi semn situatia ramane neschimbata, in cazul numerelor cu semne diferite apar probleme. Consideram ca exemplu numerele 3 si -5. Reprezentarile modul-semn, cu n=8, ale acestor numere sunt respectiv 00000011 si 10000101. Daca adunam reprezentarile dupa algoritmul clasic obtinem:

Rezultatul corespunde valorii -8, ceea ce este evident incorect. Desigur, se poate gasi un algoritm mai complex, care sa realizeze adunarea in mod corect, dar s-ar pierde din performanta, claritate si simplitate. Problema este cu atat mai serioasa cu cat adunarea sta la baza celoralte operatii aritmetice (scadere, inmultire, impartire), deci algoritmul prin care este implementata va influenta si implementarile acestor operatii.

O varianta propusa pentru rezolvarea acestei deficiente este urmatoarea:

- numerele pozitive se reprezinta in continuare la fel ca in scrierea pozitionala, cu bitul de semn avand valoarea 0

- pentru un numar negativ se porneste de la reprezentarea modulului sau, apoi fiecare bit este complementat (0 se inlocuieste cu 1 si reciproc), inclusiv bitul de semn

Se obtine astfel reprezentarea numita in complement fata de 1. Nu vom insista asupra acestei reprezentari, care are inca unele puncte slabe. Vom mentiona doar ca ea constituie un pas inainte, iar algoritmul de adunare in acest caz este apropiat de cel clasic.

In final ajungem la solutia care este folosita in sistemele de calcul actuale, numita reprezentare in complement fata de 2, care preia ideile valoroase de la variantele anterioare. Formal, reprezentarea in complement fata de 2 a unui numar intreg N este sirul de biti a_n-1a_n-2a₁a₀, cu proprietatea ca:

Desi este mai complicata decat predecesoarele sale, reprezentarea in complement fata de 2 elimina dezavantajele acestor Astfel, numarul 0 are o reprezentare unica (toti bitii cu valoarea 0), iar adunarea se face dupa acelasi algoritm ca la scrierea pozitionala, indiferent de semnul operanzilor. Ultima proprietate a fost indeplinita prin faptul ca, pentru orice numar x, daca adunam dupa algoritmul clasic reprezentarile numerelor x si -x, obtinem intotdeauna 0.

Pentru exemplificare, consideram din nou numerele 3 si -5 si n=8. Reprezentarea in cod complementar faat de 2 a numarului 3 este tot 00000011 (fiind pozitiv, este la fel ca la scrierea pozitionala), in schimb pentru numarul -5 obtinem 11111011. Adunam cele doua reprezentari dupa algoritmul clasic si obtinem:

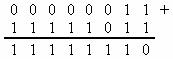
Rezultatul este reprezentarea numarului -2, deci suma a fost calculata corect.

Un aspect interesant, nu lipsit de importanta practica, este modul de obtinere al reprezentarii numarului -x pornind de la reprezentarea numarului x. Algoritmul este urmatorul:

- se parcurge sirul de biti de la dreapta la stanga

- cat timp bitii au valoarea 0, sunt lasati nemodificati

- primul bit intalnit cu valoarea 1 este de asemenea lasat nemodificat

- dupa acest prim bit cu valoarea 1, toti bitii care urmeaza (indiferent de valoarea lor) sunt inversati

Algoritmul functioneaza la fel, indiferent de semnul lui x. De exemplu, pentru numarul -5, folosit mai sus, pornim de la reprezentarea numarului 5, care este evident 00000101. Deoarece nu avem nici un bit cu valoarea 0 la extremitatea dreapta, primul bit este singurul nemodificat; toti ceilalti biti sunt inversati, deci se obtine 11111011. Este usor de verificat faptul ca, pornind de la reprezentarea lui -5, se obtine in acelasi mod reprezentarea numarului 5.

Revenim la problema domeniului reprezentabil pe un numar finit de biti. Reamintim ca, in cazul scrierii pozitionale, intervalul numerelor reprezentabile pe n biti este 0 2ⁿ-1, constand deci din 2ⁿ valori diferite consecutive. Daca folosim reprezentarea in complement fata de 2 (sau oricare alta), intervalul nu poate creste in dimensiune, din simplul motiv ca pe n biti se pot reprezenta maximum 2ⁿ valori diferite (sunt posibile 2ⁿ configuratii diferite ale sirului de biti). Astfel, intervalul valorilor reprezentabile este deplasat, incluzand atat numere negative, cat si numere pozitive. Daca analizam reprezentarea in complement fata de 2, observam ca numarul cel mai mic reprezentabil pe n biti corespunde sirului 10000, avand deci valoarea -2^n-1. In acelasi timp, cel mai mare numar reprezentabil corespunde sirului de biti 01111, avand valoarea 2^n-1-1. Rezumand, daca folosim operanzi pe n biti si reprezentarea in complement fata de 2, putem lucra cu numere in intervalul -2^n-1 2^n-1-1. De exemplu, pentru n=8 (operanzi pe un octet), putem lucra cu numere cuprinse intre -128 si 127.

1.4. Reprezentari zecimale

In mod evident, majoritatea aplicatiilor implica efectuarea de calcule cu numere reale. Pentru aceste aplicatii, reprezentarile discutate pana acum, a caror aplicabilitate este restransa la numerele naturale sau cel mult intregi, nu mai sunt suficiente. In continuare vom aborda reprezentarea numerelor cu zecimale.

Incepem prin a face o observatie importanta. Datorita caracterului finit al oricarei reprezentari, nu vom putea lucra cu adevarat cu numere reale, ci doar cu numere rationale (reamintim ca numerele irationale necesita un numar infinit de zecimale, indiferent de baza de numeratie folosita); mai mult, nu vom avea la dispozitie nici macar toate numerele rationale dintr-un anumit interval, ci doar o parte dintre aceste Vom vedea de altfel ca una dintre caracteristicile importante ale acestor reprezentari este distanta dintre doua numere reprezentabile succesive (care in cazul numerelor intregi este, desigur, 1). Totusi, in practica vom numi 'reale' numerele reprezentate in acest mod.

Ideea de pornire este una naturala: din numarul total de biti disponibil pentru o reprezentare, unii vor fi folositi pentru partea intreaga, iar restul pentru partea zecimala. Intalnim astfel aceeasi problema ca si la reprezentarea numerelor cu semn: avem nevoie de un simbol suplimentar (virgula), pe langa cele pentru cifre, simbol de care insa nu dispunem. Rezolvarea este totusi diferita, asa cum vom vedea in continuare.

Intrucat toate reprezentarile se bazeaza, in ultima instanta, pe scrierea pozitionala, reluam problema conversiei intre bazele 2 si 10, de data aceasta pentru numere zecimale. Din nou, conversia din baza 2 in baza 10 este imediata. Fie de exemplu numarul 1010010,1011₍₂₎. La fel ca in cazul numerelor naturale, avem:

1010010,1011₍₂₎ = 1 2⁶ + 0 2⁵ + 1 2⁴ + 0 2³ + 0 2² + 1 2¹ + 0 2⁰ + 1 2^-1 + 0 2^-2 + 1 2^-3 + 1 2^-4 = 82,6875₍₁₀₎

La conversia din baza 10 in baza 2, partea intreaga si partea zecimala trebuie calculate separat. Algoritmul pentru calculul partii intregi a fost deja prezentat. Pentru partea zecimala se procedeaza astfel:

Se inmulteste partea zecimala cu 2 si se retine cifra de la partea intreaga (nu poate fi decat o singura cifra semnificativa, cu valoarea 0 sau 1). Noua parte zecimala se inmulteste la randul sau cu 2, iar procesul se repeta pana cand partea zecimala devine 0. Sirul cifrelor obtinute la partea intreaga din fiecare inmultire formeaza rezultatul cautat.

De exemplu, fie numarul 309,3125₍₁₀₎. Partea intreaga, asa cum s-a vazut deja, se scrie in baza 2 sub forma 100110101. Aplicand algoritmul prezentat mai sus pentru partea zecimala, obtinem (in stanga este partea intreaga, iar in dreapta partea zecimala):

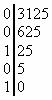
Sirul cifrelor obtinute la partea intreaga este 0101, deci 0,3125₍₁₀₎ = 0,0101₍₂₎. Ca urmare, 309,3125₍₁₀₎ = 100110101,0101₍₂₎.

O problema care apare in acest caz este posibilitatea ca unui numar finit de zecimale in baza 10 sa-i corespunda un numar infinit de zecimale in baza 2 (invers nu este posibil). Intr-un asemenea caz este evident imposibil sa obtinem o reprezentare exacta a numarului. Solutia este sa calculam atatea zecimale in baza 2 cate incap in reprezentare, obtinand astfel cea mai buna aproximare pe care o putem memor

De exemplu, fie numarul 0,3₍₁₀₎. Vom aplica din nou algoritmul de mai sus:

Este usor de observat ca partea zecimala nu va ajunge niciodata la valoarea 0, deci numarul de cifre in baza 2 necesar pentru reprezentare este infinit. Daca ne propunem sa reprezentam numarul cu 4 biti la partea zecimala, vom obtine aproximarea 0,0100₍₂₎; daca folosim 6 biti, obtinem 0,010011₍₂₎ etc.

Exista doua forme diferite de reprezentare a numerelor zecimale, care vor fi prezentate in continuare.

1.5. Reprezentari in virgula fixa

O prima solutie este ca separarea intre partea intreaga si partea zecimala a reprezentarii sa se faca intotdeauna la fel. Cu alte cuvinte, vom avea intotdeauna n biti pentru partea intreaga si m biti pentru partea zecimala, valorile pentru n si m ramanand in permanenta constante. Desigur, numarul de biti alocat unei reprezentari este n+m.

Aceasta abordare poarta denumirea de reprezentare in virgula fixa, deoarece pozitia virgulei in cadrul numarului nu se modifica. Principala consecinta este ca virgula nu mai trebuie reprezentata in mod explicit, deoarece pozitia sa, fiind mereu aceeasi, este oricum cunoscuta. Ca urmare, dispare necesitatea unui simbol suplimentar pentru virgula, deci reprezentarea pe siruri de biti este posibila.

Este usor de vazut ca reprezentarea in virgula fixa poate fi considerata o generalizare a reprezentarilor pentru numere intregi, discutate anterior. In practica se porneste de la reprezentarea in complement fata de 2, care este cea mai completa, si se decide ca un numar de biti sa fie rezervati partii intregi. Astfel, reprezentarea unui numar N pe n+m biti este sirul de biti a_n-1a_n-2a₁a₀a_-1a_-2a_-m, cu proprietatea:

Pentru a determina intervalul numerelor reprezentabile in virgula fixa pe n+m biti, ne folosim de faptul ca toate proprietatile reprezentarii in complement fata de 2 raman valabile. Reluand rationamentul de mai sus, cel mai mic numar reprezentabil corespunde sirului 10000, avand tot valoarea -2^n-1. Pe de alta parte, cel mai mare numar reprezentabil corespunde sirului de biti 01111, care acum are valoarea 2^n-1-2^-m. Intervalul numerelor reprezentabile in virgula fixa pe n+m biti este deci [ -2^n-1 , 2^n-1-2^-m ]. Reamintim faptul ca nu este vorba cu adevarat de un interval in sensul matematic al termenului, ci doar de o parte dintre numerele rationale din acel interval.

Un alt aspect important, asa cum s-a vazut mai sus, este distanta dintre doua numere reprezentabile succesive. In acest caz, trecerea de la un numar reprezentabil la urmatorul (cel imediat superior) se face intotdeauna prin adunarea reprezentarii 00001, care corespunde numarului 2^-m (cel mai mic numar strict pozitiv care poate fi reprezentat). In concluzie, distanta (numita uneori si pas) dintre doua numere reprezentabile succesive este constanta si are valoarea 2^-m.

1.6. Reprezentari in virgula mobila

Reprezentarea in virgula fixa are dezavantajul lipsei de flexibilitate. Intr-adevar, odata fixate valorile pentru n si m, s-au stabilit in mod definitiv atat ordinul de marime al numerelor reprezentabile (dat de n), cat si precizia reprezentarii (data de numarul de zecimale, adica m). Totusi, pentru aceeasi dimensiune totala a unui operand, putem prefera, de exemplu, ca in unele cazuri sa lucram cu numere mai mici, dar cu o precizie mai buna; aceasta s-ar putea realiza scazand n si crescand m, astfel incat suma lor sa ramana aceeasi. Din pacate, reprezentarea in virgula fixa nu permite asemenea adaptari, deoarece valorile n si m nu pot fi modificate. Reprezentarea in virgula mobila vine sa corecteze acest neajuns.

Ideea de pornire provine din calculul stiintific, unde se foloseste notatia cu exponent. Mai concret, un numar ca 243,59 poate fi scris sub forma 2,4359 10². Observam ca in scrierea stiintifica intervin trei elemente:

- mantisa (in cazul de fata 2,4359), care poate fi privita ca fiind 'corpul' numarului

- baza de numeratie (10)

- exponentul (2) la care este ridicata baza de numeratie

Putem deci reprezenta numarul ca o tripleta (mantisa, baza, exponent). In practica insa, baza de numeratie este mereu aceeasi, astfel incat pentru reprezentarea numarului sunt suficiente mantisa si exponentul.

Evident, pentru aceeasi baza de numeratie pot exista mai multe perechi mantisa-exponent care sa reprezinte acelasi numar. De exemplu, numarul 243,59 poate fi scris si sub forma 24,359 10¹. De fapt, se foloseste intodeauna perechea in care mantisa are exact o cifra semnificativa inainte de virgula; se spune in acest caz ca mantisa este normalizata. Avantajul acestei notatii este ca nu mai apar probleme privind numarul de biti alocat partii intregi si respectiv partii zecimale a numarului. Orice variatie in ce priveste ordinul de marime al numarului sau precizia sa se rezolva exclusiv prin ajustarea exponentului.

Structura generala a unei reprezentari in virgula mobila este urmatoarea (figura 1):

- Bitul cel mai semnificativ indica semnul numarului, dupa conventia deja cunoscuta (1 - negativ, 0 - pozitiv). Urmatoarele campuri determina modulul numarului.

- Urmatorii biti retin exponentul intr-o forma modificata, numita caracteristica.

- Restul de biti formeaza mantis

Fig. 1.

Pentru simplitate, in continuare vom nota bitul de semn cu S, exponentul cu E, caracteristica cu C, iar mantisa cu M.

Deoarece numarul poate fi supraunitar sau subunitar, rezulta ca exponentul poate fi pozitiv sau negativ. Ca atare, pentru exponentului trebuie folosita o reprezentare cu semn (separat de bitul de semn al numarului). Totusi, reprezentarea in complement fata de 2, care pare a fi prima alegere, are un dezavantaj: comparatia intre numere este relativ greoaie, deoarece se realizeaza in mod diferit in functie de semnele celor doua numere. Desi in general aceasta nu constituie o problema, in lucrul cu numere in virgula mobila, comparatia intre exponenti este o operatie executata foarte des. Din acest motiv s-a apelat la o reprezentare mai rar folosita, numita reprezentare in exces. Concret, daca avem n biti pentru exponent, atunci exponentul poate lua valori intre -2^n-1 + 1 si 2^n-1. Apoi, din exponent se obtine caracteristica prin formula C = E + (2^n-1 - 1), unde 2^n-1 - 1 este o constanta numita exces. Se observa imediat ca intodeauna C 0, deci pentru caracteristica se poate folosi scrierea pozitionala, ceea ce permite implementarea usoara a operatiei de comparare.

In privinta mantisei, reamintim ca aceasta trebuie sa fie normalizata, adica sa aiba exact o cifra semnificativa la partea intreaga. In baza 2, singura cifra semnificativa este 1, deci mantisa este de forma 1,; deoarece partea intreaga a mantisei este intotdeauna la fel, ea nu mai trebuie memorata. Ca urmare, campul M va memora numai bitii corespunzatori partii zecimale a mantisei.

Exista doua implementari practice ale reprezentarii in virgula mobila, ambele bazate pe structura prezentata mai sus, definite in standardul IEEE 754:

a) Reprezentarea in simpla precizie, care ocupa 32 biti (4 octeti), repartizati astfel:

- bitul de semn

- 8 biti pentru caracteristica

- 23 biti pentru mantisa

b) Reprezentarea in dubla precizie, care ocupa 64 biti (8 octeti):

- bitul de semn

- 12 biti pentru caracteristica

- 51 biti pentru mantisa

Cele doua variante sunt similare, diferind doar prin numarul de biti alocati diferitelor componente.

Pentru a intelege mai bine toate aceste elemente, vom considera numarul 2157,375₍₁₀₎ si vom vedea care sunt pasii care trebuie parcursi pentru a obtine reprezentarea sa in virgula mobila, simpla precizie.

- In primul rand, scriem numarul pozitional in baza 2. Aplicand algoritmii descrisi anterior pentru conversia in baza 2 a partii intregi si respectiv a partii zecimale, obtinem:

2157,375₍₁₀₎ = 100001101101,011₍₂₎

- Urmeaza scrierea sub forma de mantisa si exponent, cu mantisa normalizata:

100001101101,011 = 1,00001101101011 2¹¹

- Campul M rezulta imediat, fiind format din partea zecimala a mantisei. Deoarece mantisa are numai 14 biti semnificativi, iar campul M are 23 biti, ultimii 9 biti din M primesc valoarea 0 (sunt nesemnificativi):

M = 000011011010 11000000000

- Caracteristica se calculeaza din exponent:

E = 11 T C = E + (2⁷ - 1) = 11 + 127 = 138

Scris in baza 2, pe 8 biti: C = 10001010

- Bitul de semn are valoarea S = 0, deoarece numarul este pozitiv.

Concatenand sirurile de biti corespunzatoare celor 3 campuri, obtinem reprezentarea in simpla precizie. Deoarece numarul de biti este mare si deci dificil de controlat, in practica se prefera scrierea in baza 16, mai concisa:

01000101000001 101101011000000000₍₂₎ = 4506D600₍₁₆₎

Cateva caracteristici ale reprezentarilor in virgula mobila:

a) simpla precizie

- cel mai mic numar nenul reprezentabil (in modul): 1,175494351 10^-38

- cel mai mare numar reprezentabil (in modul): 3,402823466 10³⁸

b) dubla precizie

- cel mai mic numar nenul reprezentabil (in modul): 2,2250738585072014 10^-308

- cel mai mare numar reprezentabil (in modul): 1,7976931348623158 10³⁰⁸

O proprietate a reprezentarilor in virgula mobila de care trebuie tinut cont este faptul ca distanta dintre doua numere reprezentabile succesive nu mai este constanta, ci depinde de valoarea exponentului. Dat fiind un numar oarecare, numarul reprezentabil imediat superior se obtine adunand la mantisa valoarea minima posibila, adica 00001; in simpla precizie aceasta corespunde valorii 2^-23, iar in dubla precizie valorii 2^-51. Daca vom considera, de exemplu, reprezentarea in simpla precizie, observam ca diferenta intre cele doua numere succesive este E 2^-23, in timp ce pentru dubla precizie este E 2^-51. Rezulta de aici nu numai ca nu putem reprezenta toate numerele irationale din domeniu, dar si ca, pentru valori mari ale exponentului, exista chiar si numere intregi care nu pot fi reprezentate exact.

adunare, inmultire

2. Reprezentari alfanumerice

Informatiile prelucrate de calculator nu se rezuma la numere. Textele sunt de asemenea larg folosite, poate chiar intr-o masura mai mare, daca privim din punctul de vedere al unui utilizator obisnuit. Este deci natural sa se defineasca un mod de reprezentare pentru caractere.

O reprezentare alfanumerica asociaza fiecarui caracter o valoare unica. Asa cum am vazut, calculatorul lucreaza cu siruri de biti, organizate in octeti; dat fiind ca literele alfabetului latin (mari si mici), impreuna cu cifrele, semnele de punctuatie si cele matematice, totalizeaza mai putin de 100 de simboluri diferite, este suficient sa se aloce fiecarui caracter o valoare pe un octet. Pentru simplitate, aceste valori ale octetilor sunt  desemnate tot sub forma numerica, aceasta fiind mai accesibila si mai usor de retinut. De exemplu, nu vom spune ca unui caracter ii este asociat octetul 01101000, ci numarul (codul) 104.

O prima incercare de standardizare a reprezentarilor alfanumerice a dus la elaborarea codului EBCDIC (Extended Binary Coded Decimal Interchange Code). Deoarece insa nu au fost urmate niste principii clare in proiectare, codul EBCDIC nu s-a impus. In principal nu s-a tinut cont de faptul ca, daca lucrul cu caractere nu implica operatii aritmetice sau logice, exista totusi unele prelucrari care se aplica asupra acestora, cum ar fi comparatia, conversii intre litere mari si mici, conversii intre siruri de caractere si tipuri numerice etc.

Mult mai bine definit este codul ASCII (American Standard Code for Information Interchange), care s-a impus ca standard, fiind folosit pana astazi. In proiectarea sa au fost avute in vedere cateva aspecte care usureaza prelucrarea caracterelor:

- Literele mici au coduri consecutive, in conformitate cu ordinea alfabetica. La fel s-a procedat si in cazul literelor mari. Astfel sunt facilitate atat implementarea comparatiei intre doua caractere, care se reduce la comparatia intre doua numere naturale, cat si operatiile de testare (de exemplu, daca un caracter este litera mare sau nu).

- Cifrele au de asemenea coduri consecutive. Mai mult, ultimii 4 biti ai codului unei cifre dau exact valoarea cifrei respective, ceea ce usureaza conversia intre siruri de caractere si tipuri numerice.

Initial, codul ASCII prevedea 128 caractere. Aceasta prima versiune, care contine informatiile fundamentale necesare unei reprezentari alfanumerice, este prezentata in tabelul 1. Se observa ca primele 32 coduri sunt alocate unor caractere speciale. Acestea nu apar explicit in text, dar influenteaza modul de prezentare (dispunere in pagina) al acestuia, fiind folosite in special de catre editoarele de texte. De exemplu, codul 9 corespunde caracterului 'tab', care este folosit pentru alinierea unor parti din text.

Deoarece oricum se folosea un octet pentru memorarea unui caracter, codul ASCII a fost extins, ajungand la 256 caractere. Simbolurile nou introduse sunt in general cele folosite in limbile unor tari europene, dar care nu se regasesc in alfabetul englez (de exemplu 'á', 'a', 'ë' etc.).

Evident, nici dupa aceasta extindere codul ASCII nu putea cuprinde simbolurile tuturor scrierilor folosite in lume. Pentru a rezolva problema a fost elaborat un standard nou, numit Unicode. Acesta foloseste coduri de 2 octeti pentru caractere, ceea ce ridica numarul simbolurilor disponibile la 65536. Bineinteles, sunt incluse si codurile ASCII. Deocamdata Unicode nu s-a impus pe scara larga, fiind folosit mai ales in aplicatiile care au versiuni intr-un numar mare de limbi.

Tabelul 1.

Bibliografie

J. L. Henessy, D.  Patterson, Computer Architecture - A Quantitative Approach, Morgan Kaufmann Publishers, 1990.

D.  Patterson, J. L. Henessy, Organizarea si proiectarea calculatoarelor. Interfata hardware/software, Ed. All, 2002.

Tanenbaum, Organizarea structurata a calculatoarelor, Ed. Agora, 1999.

Tanenbaum, Modern Operating Systems, Prentice Hall, 2001.