
|
|
|
Utilizarea foilor de calcul pentru rezolvarea problemelor de programare liniara
Foile de calcul sunt instrumente utilizate frecvent pentru prelucrarea datelor in multe organizatii. Deoarece modelele matematice necesita de multe ori date care deja exista in alte foi de calcul, este important a intelege modul in care o problema de programare liniara poate fi rezolvata cu ajutorul foilor de calcul. In continuare vom ilustra modul in care se poate rezolva problema precedenta folosind foile de calcul. In acest scop va fi folosit programul de calcul tabelar Microsoft Excel.
Un model de programare liniara transpus intr-o foaie de calcul va contine urmatoarele elemente:
Celulele care contin datele problemei.
Celulele pentru variabilele de decizie.
O celula care contine formula pentru calcularea functiei obiectiv.
Celulele care contin formulele pentru calcularea partii stangi a restrictiilor.
Celulele care contin valorile partii drepte a restrictiilor.
Transpunerea problemei intr-o foaie de calcul presupune parcurgerea urmatoarelor etape:
Introducerea datelor problemei in foaia de calcul.
Definirea celulelor care vor contine variabilele de decizie.
Definirea celulei care contine formula pentru functia obiectiv.
Definirea celulelor care contin formulele din partea stanga a restictiilor.
Definirea celulelor care contin valorile din partea dreapta a restrictiilor.
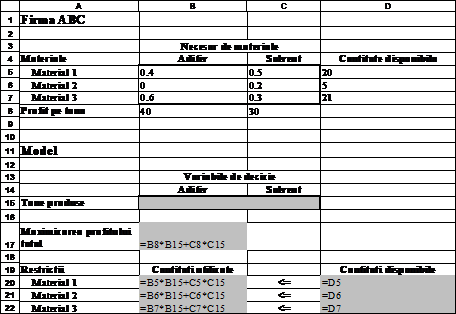
In figura II.1.2
este prezentata solutia pentru problema prezentata anterior.
Figura II.1.2 – Foaia de calcul utilizata pentru rezolvarea problemei
Remarcati ca foaia de calcul este alcatuita din doua parti: o parte contine datele problemei si alta contine modelul. Un avantaj al separarii datelor de model este ca se poate studia efectul modificarii marimilor de intrare asupra modelului facand modificari doar in zona care contine date. Un alt avantaj este ca analistul poate dezvolta modelul independent de datele disponibile.
In continuare este prezentat fiecare pas al procedurii:
Pasul 1: Introducerea datelor problemei. Datele problemei apar in partea superioara a foii de calcul. Fractiile care reprezinta compozitia pentru obtinerea unei tone de solvent si aditiv au fost convertite in valori zecimale si introduse in domeniul B5:C7. Valoarea 0.4 din celula B5 arata ca fiecare tona de aditiv produsa utilizeaza 0.4 tone de material 1, valoarea 0.5 din celula C5 arata ca fiecare tona de solvent produsa utilizeaza 0.5 tone de material 1, etc. Celulele D5:D7 contin cantitatea disponibila din fiecare material, iar celulele B8 si C8 contin profitul obtinut prin vanzarea unei tone de aditiv (40$), respectiv solvent (30$).
Pasul 2: Definirea celulelor care vor contine variabilele de decizie. Celulele B15 si C15 contin numarul de tone de aditiv si solvent produse.
Pasul 3: Definirea celulei care contine formula functiei obiectiv. Celula B17 contine formula pentru calcularea functiei obiectiv: ˆ B8*B15‡ C8*C15 (profiul unitar pe tona de aditiv * productia de aditiv ‡ profiul unitar pe tona de solvent * productia de solvent).
Pasul 4: Definirea celulelor care contin formulele din partea stanga a restrictiilor. Celulele B20:B22 contin formulele care indica cum se calculeaza partea stanga a restrictiilor. Pentru materialul 1, in celula B20 se introduce formula ˆB5*B15‡C5*C15 (cantitatea de aditiv produsa*cantitatea de material 1 pentru a produce o tona de aditv ‡ cantitatea de solvent produsa*cantitatea de material 1 pentru a produce o tona de solvent). In mod similar se vor introduce in celulele B21 si B22 formulele pentru materialele 2 si 3.
Pasul 5: Definirea celulelor care contin valorile din partea dreapta a restrictiilor. In problema analizata valorile din partea dreapta a restrictiilor reprezinta cantitatile de material disponibile, valori care deja sunt introduse in domeniul D5:D7. Pentru materialul 1, in celula D20 se introduce formla ˆD5, pentru matrialul 2, in celula D21 se introduce formula ˆD6, iar pentru materialul 3 in celula D22 se introduce formula ˆD7.
Un avantaj al folosirii foilor de calcul este ca daca una din valorile din partea care contine datele problemei se modifica, valorile din model se modifica automat..
Pentru a determina solutia optima a problemei se va folosi Solver-ul din Excel. Pasii urmatori arata modul in care poate fi folosit Solver-ul pentru obtinerea solutiei optime pentru o problema de programare liniara.
Se selecteaza meniul Tools.
Se aplica comanda Solver.
Caseta Solver Parameters se completeaza in modul urmator:
Set Target Cell: B17
Se selecteaza optiunea Max.
By Changing Cells B15:C15.
Se selecteaza butonul Add.
Caseta Add Constraint se completeaza astfel:
Cell Reference B20:B22
Se selecteaza operatorul
Constraint D20:D22
Se selecteaza butonul OK.
Cand caseta Solver Parameters apare din nou se selecteaza butonul Options.
In caseta Solver Options se selecteaza:
Assume Linear Model.
Assume Non- Negative
Butonul Ok.
Cand caseta Solver Parameters apare din nou se selecteaza butonul Solve.
In caseta Solver Results se selecteaza Keep Solver Solution. Se selecteaza butonul Ok pentru a genera solutia optima, afisata in celulele B15, C15.
Solutia optima este 25 tone de aditiv si 20 tone de solvent.