
|
|
|
Grafuri neorientate
Incadrarea unitatii in programa scolara: se studiaza in clasa a XI-a la specializarea Matematica-Informatica intensiv informatica si la clasa a XI-a la specializarea Matematica-Informatica neintensiv, la disciplina Informatica.
Continutul stiintific:
Se numeste graf neorientat, o pereche ordonata de multimi notata G=(X,U), unde X= este o multime finite si nevida de elemnte numite noduri sau varfuri, iar U= este o multime de perechi neordonate de elemente din X numite muchii.
Un graf poate fi reprezentat sub forma unei figuri geometrice alcatuite din puncte (care corespund varfurilor) și din linii drepte sau curbe care unesc aceste puncte (care corespund muchiilor sau arcelor).
Exemplu:
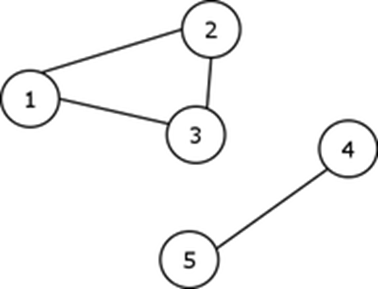
G=(X,U)
X =
U =
Definitii (notiuni introductive):
Muchii adiacente = doua muchii cu o extremitate comuna. Pentru exemplul de mai sus, muchiile [1,2] si [2,3] sunt muchii adiacente pentru ca au ca extremitate comuna nodul 2.
Graful partial al grafului G=(V,U) este un graf G1=(V,U1) astfel incat U1este inclus in U, adica G1 are aceeasi multime de varfuri ca G, iar mutimea de muchii U1 este chiar U sau o submultime a acesteia (un graf partial al unui graf se obtine pastrand aceeasi multime de noduri si eliminand o parte din muchii).
Un subgraf al unui graf G=(V,U) este un graf H(V1,U1) astfel incat V1 este inclus in V iar U1 contine toate muchiile din U care au ambele extremitati in V1 (un subgraf se obtine eliminand varfuri din V si muchiile incidente acestor varfuri). Vom spune ca subgraful H este indus sau generat de multimea de varfuri V1.
Gradul unui varf x este numarul muchiile incidente cu x. Gradul varfului x se noteaza d(x).
Un varf care are gradul 0 se numeste varf izolat.
Un varf care are gradul 1 se numeste varf terminal.
Se numeste graf complet cu n varfuri un graf care are proprietatea ca orice doua noduri diferite sunt adiacente.
Un graf complet Kn are n(n-1)/2 muchii.
Un graf G=(V,U) se numeste bipartit daca exista doua multimi nevide A, B astfel incat V=A U B, A∩B = si orice muchie a lui G are o extremitate in A iar cealalta in B.
Un graf bipartit se numeste complet daca pentru orice x din A si y din B, exista muchia (x,y).
Reprezentarea grafurilor
1). Matricea de adiacenta
Este o matrice patratica cu n linii si n coloane, in care elementele a[i,j] se definesc astfel: a[i,j]=1 daca exista (i,j) in U, cu x diferit de y si 0 daca nu exista (i,j) in U.
- Matricea de adiacenta este simetrica fata de diagonala principala: A(i,j)=A(j,i).
- Gradul unui varf x se poate determina calculand suma pe linia x.
Ex: Pentru graful G=(X,U) din figura de mai sus, matricea de adiacenta este:
0 1 1 0 0
A = 1 0 1 0 0
1 1 0 0 0
0 0 0 0 1
0 0 0 0 1
3). Lista de adiacenta:
Pentru fiecare nod punem in evidenta multimea nodurilor cu are formeaza muchii. Pentru exemplul din figura de mai sus, lista de adiacenta corespunzatoare grafului este:
Varf | Lista nodurilor adiacente
1 2,3
2 1,3
4 5
5 4
4).Vectorului de muchii;
Fiecare muchie a grafului poate fi privita ca o inregistrare cu doua componente: cele doua varfuri care constitue extremitatile muchiei.
-Un graf complet cu n varfuri are n*(n-1)/2 muchii.
-Se numeste graf complet cu n varfuri, notat Kn, un graf G=(X,U) cu proprietatea ca intre oricare doua varfuri exista o muchie
Ex: Pentru graful din figura de mai sus avem;
V=
U=
Conexitatea((lant, ciclu, graf conex, componenta conexa
Se numeste lant in G succesiunea de varfuri L=[xi1,xi2,,xik] cu proprietate ca orice doua noduri consecutive din lant sunt adiacente, adica [xi1,xi2], [xi2,xi3], , [xik-1,xik]
Daca varfurile xi1, xi2, , xik sunt diferite doua cate doua atunci lantul se numeste lant elementar. In caz contrar, lantul este lant neelemntar. Cu alte cuvinte, un lant elementar este un lant care nu trece de doua ori prin acelasi varf.
Se numeste ciclu in G un lant L pentru care xi1=xik si toate muchiile adiacente [xi1, xi2], [xi2, xi3], , [xik-1, xik] sunt diferite.
Se numeste ciclu elementar un ciclu care are proprietate ca oricare doua varfuri ale sale, cu exceptia primului si ultimului, sunt diferite doua cate doua. In caz contrar, ciclul este un ciclu neelementar.
Un graf G se numeste conex daca pentru orice doua varfuri x si y diferite ale sale exista un lant ce le leaga.
Se numeste componenta conexa a grafului G=(V,U) un subgraf G1=(V1,U1), conex, al lui G care are proprietatea ca nu exista nici un lant care sa lege un varf din V1 cu un varf din V-V1. Cu alte cuvinte, se numeste componenta conexa a unui graf neorientat, G = (V,U), un subgraf al lui G, G1=(V1,U1), conex si maximal.
Grafuri hamiltoniene si euleriene
Se numeste ciclu hamiltonian intr-un graf, un ciclu elementar care contine toate varfurile grafului.
- Un graf care contine un ciclu hamiltonian se numeste graf hamiltonian.
Un lant elementar care contine toate varfurile grafului se numeste lant hamiltonian.
Un graf hamiltonian are cel putin trei varfuri
- Graful complet cu n varfuri este un graf hamiltonian.
Teorema: Fie G=(X,U), cu n>=3 varfuri, daca oricare ar fi x un nod al grafului si d(x)>=n/2, atunci graful este hamiltonian.
Se numeste ciclu eulerian intr-un graf, un ciclu care contine toate muchiile grafului.
Un graf care contine un ciclu eulerian se numeste graf eulerian.
- Un lant eulerian este un lant care contine toate muchiile grafului.
Teorema: Un graf fara varfuri izolate este eulerian, daca si numai daca este conex si gradele tuturor varfurilor sunt numere pare.
Parcurgerea grafurilor
Prin parcurgerea grafurilor neorientate se intelege vizitarea varfurilor intr-o anumita ordine, ordine data de un anumit criteriu.
Exista doua metode de parcurgere:
1) Breadth First
Prin algoritmul BF se realizeaza o parcurgere a grafului "in latime".
Se viziteaza un varf initial s, apoi vecinii sai (varfurile adiacente cu s), dupa aceea vecinii vecinilor lui s (nevizitati inca ) etc. Daca graful nu este conex nu se pot vizita toate varfurile.
Ex: Pt graful de mai sus parcurgere in latime pornind de la nodul 1: 1 2 3
Algoritm:
Pas1 : Pentru i:=1, n executa viz[i];=0
Pas2: c[1]:=x; viz[x]:=1
Pas3: p:=1; u:=1
Pas4: Cat timp p<=u executa
Pas4.1 v:=c[p]; p:=p+1
Pas4.2 Pentru toti vecinii i a lui v nevizitati inca executa
u:=u+1; c[u]=i
viz[i]:=1
2) Depth First
Algoritmul DF se caracterizeaza prin faptul ca realizeaza o parcurgere a grafului "in adancime" atat cat este posibil.
Parcurgerea incepe cu un varf s ales initial. Prelucrarea unui varf conduce la prelucrarea primului sau
vecin inca nevizitat, apoi se prelucreaza primul vecin al acestuia care nu a fost inca vizitat etc. Se observa un procedeu recursiv de parcurgere a grafului. Aceasta tehnica de parcurgere conduce la efectuarea unui numar relativ mare de apeluri recursive inainte de a se intoarce dintr-un apel.
Ex: Prntru graful de mai sus parcurgere in adancime pornind de la nodul 3: 3 1 2
Algoritm:
Pas1 Pentru i:=1,n executa viz[i]=0
Pas2 st[i]:=x; viz[x]:=1; scrie x
Pas3 k:=1
Pas4 Cat timp k>0 executa
Pas4.1 v:=st[k]
Pas4.2 Caut primul succesor nevizitat al lui v(fie acesta y)
Pas4.3 Daca nu exista atunci k:=k-1
Altfel scrie y; viz[y]=1;
k:=k+1; st[k]=y;
Tipuri de exercitii
- algoritmi simpli pt insusirea terminologiei si prop. Grafurilor : calcularea gradelor varfurilor unui graf, verificarea faptului ca o succesiune de varfuri reprezinta lant, drum, ciclu sau circuit in graf, identificarea tuturor ciclurilor de lungime 3 intr-un graf, verificarea proprietatii de graf complet etc.
- probleme practice, cum ar fi: conectarea unor calculatoare in retea astfel incat costurile de conectare sa fie minime; Determinarea unui traseu de lungime minima intre doua localitati;Determinarea unei modalitati de transmitere a unui mesaj intr-o interretea astfel incat numarul total de servere prin intermediul carora este transmis mesajul sa fie minim; Determinarea structurii relationale a unui grup de persoane
Metode de predare-invatare eficiente:
Conversatia cunostintele sunt vehiculizate prin intermediul dialogului(intrebari si raspunsuri), discutiilor sau dezbaterilor. Pe parcursul lectieieaa se floseste in toate etapele acesteia; verificare, tarnsmitere si fixare.
Exercitiul este modalitatea de efectuare rapida a actiunilor de invatare teoretica si practica, in vederea fixarii si consolodarii cunostintelor dobandite si a formarii si dezvoltarii priceperilor si deprinderilor intelctuale si aplicative.
Invatarea prin descoperire: consta in punerea elevilor in situatia de a descoperi solutia unei probleme prin efort propriu, de obicei sub indrumarea profesorului.
Dificultati si greseli posibile intampinate de elevi:
Dificultati in inteelegerea notiunii de lant si ciclu al unui graf;
dificultati in intelegerea algoritmilor de parcurgerea grafurilor
dificultati in stabilirea daca un graf este hamiltonian sau eulerian;