Calculul integralei definite pe un interval [a,b], folosind metodele trapezelor, Simpson si Gauss

Universitatea Tehnica Cluj-Napoca

Facultatea de Automatica si Calculatoare

Sectia Calculatoare

Calculul integralei definite pe un interval [a,b], folosind metodele trapezelor, Simpson si Gauss

Notiuni teoretice

Schema logica

Metoda trapezelor (foloseste o aproximare liniara a functiei):

Algoritm:

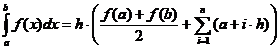
i : integer;

h,s : real;

h := (b-a)/n;

s := (f(a)+f(b))/2;

for i:=1 to n do

s := s + f(a+i*h);

endfor;

s := s*h;

Metoda Simpson (foloseste o aproximare parabolica a functiei):

Algoritm:

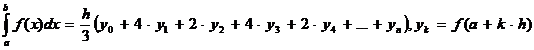
sumsf, sumimpar, sumpar : integer;

h, simpson,x : real;

n,j, k : integer;

sumsf : = f(a) + f(b);

sumimpar := 0;

sumpar := 0;

for j :=1 to 9 do

begin

n := 2^j;

h := (b-a)/n;

sumpar := sumpar + sumimpar;

sumimpar = 0.0;

k := 1;

while (k <= n-1)

begin

x = a + k*h;

sumimpar := sumimpar + f(x);

k := k+2;

end;

endwhile;                   

simpson := h*(sumsf + 4*sumimpar + 2*sumpar)/3;

end;

endfor;

OBS: pentru n = 10

- sumpar reprezinta y₂, y₄, y₆, y₈, y₁₀,

- sumimpar reprezinta y₁, y₃, y₅, y₇, y₉,.

- sumpsf reprezinta y₀, y₂, y₄, y₆, y₈,.

(y_i - imaginile functiei la pasul i)

Implementare

Programul este structurat in trei fisiere: programul principal (INTEGR.CPP), fisierul header care contine functia de integrat (FUNC.H) si fisierul header care contine metodele de integrare (INTGRMET.H)

1. INTEGR.CPP

Procedura principala este cuprinsa intr-un ciclu do-while , care la fiecare pas sterge ecranul, afiseaza optiunile, valideaza optiunea introdusa, citeste capetele intervalului, si, in functie de optiune, se apeleaza functia utilizata la integrare (in corpul instructiunii switch). In cazul metodei trapezelor se cere si pasul.

Mai departe se cere confirmare pentru continuarea programului, valoarea introdusa ca raspuns este retinuta in variabila exit, care este evaluata in corpul instructiunii while, cand aceasta ia valoarea 'n', programul se termina.

2. FUNC.H

Acest fisier contine functia care urmeaza a fi integrata. Aceasta s-a separat de restul programului pentru a fi usor de modificat. Aici se pot introduce functii care apar in biblioteca Borland C++ 3.1.

3. INTGRMET.H

In acest fisier s-au implementat procedurile de integrare prin cele doua metode. Functia double trapez(double (*f)(double), double a, double b,int n) integreaza functia f prin metoda trapezului, pe intervalul [a,b], impartind acest interval in n subintervale egale.

Functia double simpson(double (*f)(double), double a, double b) integreaza functia f prin metoda Simpson, numarul de subintervale fiind calculate in interirul ei.

Codul sursa

//FUNC.H :

// aici se defineste functia ce urmeaza a fi integrata

// dupa 'return' introduceti functia

double f(double x)

//INTGRMET.H :

// Functiile care integreaza functia data prin 3 metode

// 1. Metoda trapezelor

double trapez(double (*f)(double), double a, double b,int n)

// 2. Metoda Simpson

double simpson(double (*f)(double), double a, double b)

simpson = h*(sumsf + 4.0*sumimpar + 2.0*sumpar)/3.0; //se calculeaza suprafata cu sumpar si sumimpar actualizate

}

return simpson;

//INTEGR.CPP

#include <conio.h>

#include <stdio.h>

#include <ctype.h>

#include <math.h>

#include 'func.h' // functia de integrat

#include 'intgrmet.h' // functiile de integrare numerica

void main()

switch (opt)

break;

case '2':

break;

default:

break;

}

clrscr();

puts('ttContinuati? [d/n]'); // se cere confirmarea pentru a continua programul

exit=getch();

}while(exit == 'd'); // se iese daca utilizatorul a ales caracterul 'd'

}

Comparare metode

Metoda trapezelor

Aceasta metoda foloseste aproximarea liniara, calculandu-se ariile trapezelor formate sub grafic, graficul fiind aproximat cu drepte de lungime egala pe axa OX. Precizia sa este dependenta de numarul n de subintervale in care se imparte intervalul [a,b]. Metoda este mai rapida decat in cazul metodei Simpson.

Eroarea:

Metoda Simpson

Metoda foloseste aproximarea parabolica, pe o curba de gradul 2, apropiindu-se mai mult de graficul functiei decat in cazul formulei trapezelor, precizia se calculeaza in interiorul functiei. Calculul integralei ia mai mult timp decat in cazul metodei trapezelor.

Eroarea:

Exemple

Metoda trapezelor

f(x)=sin(x); interval [0,10], n=10 => 1,6831

f(x)=sin(x); interval [0.10], n=100=>1,83754

f(x)=x⁴-2x³-4x, interval [10, 20], n=10=>546583

f(x)=x⁴-2x³-4x, interval [10, 20], n=100=>544421,833

f(x)=ln(x²+2x+1), interval [0,1], n=10=>0,77176

f(x)=ln(x²+2x+1), interval [0,1], n=100=>0,77258

Metoda Simpson

f(x)=sin(x); interval [0,10] => 1,8397

f(x)=x⁴-2x³-4x, interval [10, 20] =>54400

f(x)=ln(x²+2x+1), interval [0,1] =>0,77259

Bibilografie

1.Ion Simionescu, Mihai Dranga, Victor Moise, Metode Numerice in Tehnica, Editura Tehnica, Bucuresti 1995

2. Horia Georgescu, Octavian Basca, Programe in limbajulFORTRAN, Editura Albatros, Bucuresti 1975

3. Theodor Balan, Algoritmi si Programe Windows, Editura Tehnica, Bucuresti 2000

4. Sorin Mitran, Corneliu Berbente, Silviu Zancu, Metode Numerice, Editura Tehnica