Baze de date - Definirea modelului relational, Normalizarea relatiilor, Nivelul intern (fizic), Proiectarea bazei de date

1.     Definirea modelului relational

2.     Normalizarea relatiilor

3.     Nivelul intern (fizic)

4.     Proiectarea bazei de date

Modelul relational are la baza conceptul de relatie definit in teoria matematica a multimilor, ca fiind o submultime a produsului cartezian al mai multor multimi:

Familia de multimi pe care este definita relatia se numeste domeniu, iar daca M₁ = M₂ = . = M_n, relatia este omogena. Numarul n se numeste gradul relatiei (aritatea relatiei), un element al relatiei t = (m₁, m₂, . , m_n) este numit tuplu, iar numarul de tupluri indica cardinalul relatiei.

Relatiile se reprezinta intr-o forma simpla prin tabele.

Prelucrarea relatiilor se face prin algebra relationala

Operatorii relationali se pot grupa in operatori de baza, care pot genera toata clasa operatorilor relationali si operatori auxiliari. Operatorii relationali de baza se impart in operatori de asamblare si operatori unari.

Operatorii de asamblare sunt operatori binari, care primesc la intrare 2 relatii si genereaza la iesire o singura relatie. Acestia sunt: reuniunea, diferenta si produsul cartezian, care au aceeasi semnificatie ca si in teoria multimilor. Operatorii unari se aplica asupra unei relatii si genereaza o alta relatie. Din aceasta clasa fac parte proiectia si selectia.

Proiectia relatiei R de schema R (A₁, A₂, . , A_n) dupa atributele A_i1, A_i2, . , A_ip (i_i i_k si p < n) este relatia R' de schema R' (A_i1, A_i2, . , A_ip), ale carei tupluri se obtin prin eliminarea valorilor atributelor din R care nu apar in R' si prin suprimarea dublurilor.

R' = P A_i1, A_i2, . , A_ip (R)

Altfel spus, prin intermediul proiectiei, dintr-un tabel cu un anumit numar de coloane se obtine unul cu un numar mai mic de coloane.

Selectia relatiei R fata de criteriul Q este relatia R' cu aceiasi schema ca si R, ale carei tupluri satisfac criteriul (predicat).

Q = A_i1 q₁ C₁ L A_i2 q₂ C₂ L A_ip q_p C_p, unde q_i < > , C_i - constante

Altfel spus, prin operatorul de selectie, dintr-un tabel cu un anumit numar de coloane se obtine unul cu aceleasi coloane, dar cu un numar mai mic de rinduri.

Operatorii auxiliari pot fi dedusi din setul de operatori de baza si sunt: compunerea (Join), intersectia si impartirea (diviziunea). Compunerea conditionala (Join) a doua relatii R1 si R2 dupa calificatorul multi -atribut Q este relatia E ale carei tupluri sunt cele ale produsului cartezian R1 x R2 care satisfac calificatorul Q. Functie de calificatorul Q se disting mai multe tipuri de compuneri:

q      daca Q este de forma A_i = B_j , se numeste echicompunere;

q      daca Q este de forma A_i q B_j : unde q < > se numeste q compunere, si poate fi exprimata in functie de operatorii de baza.

q      daca Q este de forma A_i = A_j se numeste autocompunere.

Privita prin prisma modelului relational, baza de date apare ca o colectie de relatii (tabele) normalizate, in care fiecare coloana reprezinta un atribut distinct iar fiecare rand un tuplu distinct. Tuplurile unei relatii se pot identifica in mod unic prin intermediul valorilor unuia sau mai multor atribute (eventual toate atributele), care joaca rol de cheie primara a relatiei respective. Se numeste domeniu primar, un domeniu pe care este definit un singur atribut drept cheie primara. Dandu-se doua relatii R₁ si R₂ cu atributele A₁ si A₂ chei primare definite pe acelasi domeniu primar D, spunem ca A₁ este cheie externa, daca utilizand o parte din valorile ei sau toate, putem regasi tuplurile relatiei R₂. Altfel spus, un atribut al unei relatii este cheie externa, daca se regaseste pe post de cheie primara intr-o alta relatie.

Deoarece relatiile reflecta un anumit aspect din realitate, acestea se supun unor restrictii care sunt de doua tipuri:

q      restrictii de integritate care depind de semantica valorilor domeniilor si care cer ca relatiile sa se supuna urmatoarelor reguli:

integritatea entitatii, prin care valorile cheii primare trebuie sa fie diferite de zero; altfel cheia nu va mai fi identificator;

integritatea referirii, potrivit careia valorile unei chei externe trebuie sa refere tuplurile unei alte relatii sau sa fie nedefinite.

q      alte restrictii care se aplica asupra tuplurilor relatiei si nu asupra domeniilor, reflectand anumite corelatii de ordin valoric (egalitate, inegalitate).

E. F. Codd, a aratat ca intr-o anumita forma relatiile poseda proprietati nedorite, pe care le-a numit anomalii de actualizare:

q      Anomalia de stergere

q      Anomalia de adaugare

q      Anomalia de modificare

Pentru a inlatura aceste anomalii, Codd a stabilit trei forme normale pentru relatii si a introdus procesul de normalizare care se bazeaza pe notiunea de dependenta functionala (FD) ca relatie intre atributele unei entitati ce are un caracter invariant.

Fie date doua atribute D si E si notam domeniul valorilor lui D cu DOM (D) si domeniul valorilor lui E cu DOM (E) si o functie f: DOM (D) DOM (E) Spunem ca f este o dependenta functionala, daca pentru ( ) d I DOM (D) distinct ii corespunde o singura valoare e I DOM (E). Atributul D se numeste "determinantul" dependentei, iar dependenta se simbolizeaza D E. Dependenta functionala poate fi generalizata pe mai multe atribute: f: A₁, A₂, ., A_n B₁, B₂, ., B_m unde A₁, A₂, ., A_n se numeste "partea stanga" iar B₁, B₂, ., B_m se numeste "partea dreapta" a FD-ului.

O dependenta functionala f: DOM (D) DOM (E) este elementara (completa), daca nu exista o alta dependenta f': DOM (D') DOM (E), unde DOM (D') DOM (D) sau, altfel spus, daca "partea stanga" nu mai poate fi descompusa astfel incat rezultatul obtinut sa fie tot o dependenta functionala. Daca f: D₁, D₂,., D_m, D_{m + 1}, . , D_n E si g: D₁, D₂,., D_m E sunt doua FD-uri, unde m < n, atunci atributele D_{m + 1}, . , D_nse numesc atribute superflue pentru f, deoarece atributele D₁, D₂,., D_m sunt suficiente pentru a-l determina functional pe E. In aceasta situatie spunem ca E este dependent partial de D₁, D₂,., D_n.

Fie R [A₁, A₂,., A_n] o relatie si K o submultime a multimii de atribute (K . Spunem ca submultimea K este cheie primara pentru relatia R daca sunt indeplinite urmatoarele conditii:

q      ) A_i K, A_i este dependent functional pe K;

q      ) K' K, A_i nu este dependent functional pe K'.

Armstrong a introdus un set de axiome si reguli de inferenta, care permit prelucrarea dependentelor functionale. Notand cu M multimea atributelor relatiei R, axiomele lui Armstrong sunt:

A1. Reflexivitatea: daca A B M T A B;

A2. Cresterea: daca A B si X M T AX BX;

A3. Tranzitivitatea: daca A B si B C T A C.

Din cele trei axiome rezulta urmatoarele reguli de inferenta:

R1. Reuniunea: daca A B si A C T A BC;

R2. Pseudotranzitivitatea: daca A B si XB C T AX C;

R3. Descompunerea: daca A BC T A B si A C.

O relatie este in forma normala 1 (1NF), daca si numai daca toate atributele ei contin numai valori atomice (fig. 1.a.).

Cheia primara a relatiei R este compusa din P# si B#, iar atributele U, X, C, L si T nu sunt complet dependente functional de aceasta. De asemenea perechile de atribute (L, C) si (L, T) sunt mutual dependente. Aceasta relatie poseda anomaliile de actualizare prezentate mai inainte, de exemplu:

q      nu putem adauga un tuplu pentru care nu cunoastem beneficiarul (B#) si localitatea (L), deoarece conform regulii de integritate a entitatii nici o componenta a cheii primare (P#, B#) nu poate fi nula;

q      daca produsul P5 nu mai poate fi fabricat temporar, deci trebuie sters tuplul (P5, buc, 30, 10, B₂, Ploiesti, 500, 244), inseamna ca se pierd si informatiile despre beneficiarul B₂, care mai sunt necesare in continuare;

q      daca dupa o perioada de timp intervine o schimbare a preturilor produselor, modificarea acestora se face greu datorita faptului ca acelasi pret intervine in mai multe tupluri (redundanta mare).

q     

Pentru a inlatura anomaliile de actualizare, utilizand operatorul de proiectie, descompunem relatia R in trei relatii R1, R2 si R3 (fig. 1.b.) care sunt in forma normala 2 (2NF) si care conserva datele din relatia R.

O relatie este in forma normala 2 (2NF) daca si numai daca este in 1NF si orice atribut noncheie este complet dependent functional de cheia primara.

Analizand diagrama dependentelor functionale asociata relatiei R3 din fig. 1. b, observam existenta dependentelor tranzitive B# L, L  C si B# L, L T care genereaza si ele anomalii de actualizare, cum sunt:

q      daca stergem tuplul referitor la beneficiarul B1 (B1, Brasov, 400, 268) se pierd si datele referitoare la localitatea, codul postal si prefixul telefonic, care mai sunt necesare;

q      modificarea codului postal (C) se face greu, datorita faptului ca aceiasi valoare apare in mai multe tupluri (redundanta mare);

q      nu putem adauga o noua localitate daca nu exista cel putin un beneficiar din localitatea respectiva.

Pentru a inlatura aceste anomalii, descompunem relatia R3 in doua relatii R₃₁ si R₃₂ (fig. 1.c.) care sunt in forma normala 3NF.

O relatie este in forma normala 3 ( 3NF ) daca si numai daca este in 2NF si fiecare atribut noncheie nu este dependent tranzitiv pe cheia primara. Relatiile R₁, R₂, R₃₁ , R₃₂ sunt in forma normala 3.

Considerand relatia A definita pe atributele: localitate (L), strada (S) si codul postal (C); cheia relatiei poate fi LS sau SC, iar multimea dependentelor functionale este: F = . Conform definitiei, relatia A este in 3NF si are doua chei candidate LS si SC. Analizand mai atent aceasta relatie, se observa ca nu putem adauga o localitate noua cu codul postal asociat daca nu specificam o adresa din localitatea respectiva, iar stergerea unei strazi implica si stergerea localitatii si a codului postal. Deci relatia A prezinta anomalii la operatiile de adaugare si stergere, ceea ce denota ca forma normala trei nu manuieste satisfacator relatiile cu doi sau mai multi chei candidate.

Pentru a inlatura aceste anomalii, a fost introdusa forma normala Boyce - Codd (BCNF), (mai tare decat 3NF), potrivit careia o relatie A cu multimea dependentelor functionale F este in BCNF daca pentru orice dependenta (X Y) I F cu Y X, X include o cheie, a relatiei A. Conform acestei definitii relatia A (L, S, C) cu F = nu este in BCNF din cauza dependentei C L, unde C nu este cheie pentru A.

Avantajele modelului relational

Facand o analiza a modelelor nerelationale comparativ cu modelul relational rezulta urmatoarele avantaje in favoarea celui din urma:

q      modelul relational este un model simplu care permite utilizatorului sa vada baza de date ca o colectie de tabele (relatii) - o reprezentare mentala larg accesibila atat informaticienilor cat si neinformaticienilor;

q      asigura independenta fizica si logica a programelor de prelucrare fata de structura datelor, eliminand din schema conceptuala si schemele externe toate detaliile privind structura de memorare si strategiile de acces;

q      operatia de normalizare introdusa de modelul relational asigura gasirea structurii optime a datelor prin inlaturarea anomaliilor de actualizare si diminuare a redundantei.

q      Prin introducerea notiunilor de dependenta functionala, dependenta multivaloare si dependenta jonctiune modelul relational depaseste stadiul limitat al reprezentarii datelor in calculator, avansand spre formalizarea elementelor de semantica ce guverneaza domeniul informatiilor;

q      este un model omogen, deoarece reprezinta legaturile si asocierile dintre relatii tot prin relatii, spre deosebire de modelele ierarhic si retea care utilizeaza in acelasi scop conexiunea si respectiv setul.

q      suplete in comunicare cu utilizatorul neinformatician prin intermediul unor limbaje neprocedurale de nivel inalt.

Nivelul intern (modelul fizic) este cel ce corespunde structurii in care sunt stocate datele in interiorul masinii. Sunt specificate tabelele (fisierele) care le contin (nume, organizare, localizare etc.), componentele fiecarui fisier (lungime, campuri, plasare a acestora in cadrul fisierului), caile de acces la componentele tabelelor (indecsi, relatii, legaturi intre tabele).

Se vor avea in vedere cerintele privind asigurarea protectiei datelor, atat din punct de vedere al continutului campurilor din tabele (verificarea si validarea valorilor campurilor la introducere, evitarea stergerii, din greseala sau din rea vointa, a datelor importante, cu secvente de program special concepute), cat si in ceea ce priveste accesul utilizatorilor la baza de date (stabilirea drepturilor de acces trebuie sa se faca tinand cont de rolul, functia si sarcinile fiecarui utilizator).

Proiectarea unei baze de date presupune realizarea modelelor conceptual, logic si fizic, prin trecerea de la MCD la MLD, apoi de la MLD la MFD.

MLD se obtine aplicand regulile de trecere de la MCD la MLD.

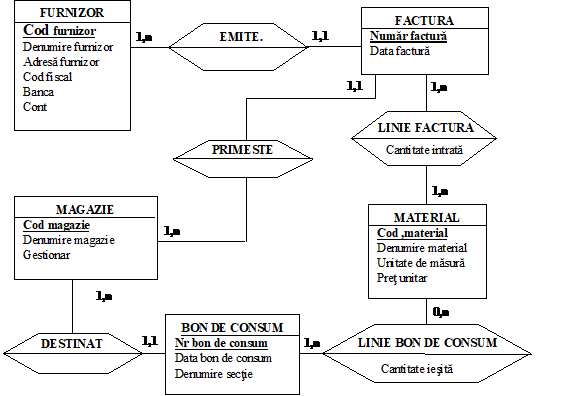
Modelul conceptual al datelor

Modelul logic (relational) al datelor

Furnizor (Cod furnizor, Denumire furnizor, Adresa furnizor, Cod fiscal, Banca, Cont)

Factura (Numar factura, Data factura, Cod furnizor, Cod magazie)

Magazie (Cod magazie, Denumire magazie, Gestionar)

Linie factura (Nr linie factura, Numar factura, Cod material, Cantitate intrata)

Material (Cod material, Denumire material, Unitate de masura, Pret unitar)

Linie bon de consum (Nr linie bon de consum, Nr bon de consum, Cod material, Cantitate iesita)

Bon de consum (Nr bon de consum, Data bon de consum, Denumire sectie, Cod magazie)