
|
|
|
Elemente de baza ale limbajului Prolog
Inceputul programarii logice poate fi atribuit lui R. Kowalski si A. Colmerauer si se situeaza la inceputul anilor '70. Kowalski a plecat de la o formula logica de tipul:
S1 S2 Sn S
care are, in logica cu predicate de ordinul intai, semnificatia declarativa conform careia S1 S2 Sn implica S, adica daca S1 si S2 si Sn sunt fiecare adevarate atunci si S este adevarat, si a propus o interpretare procedurala asociata. Conform acestei interpretari, formula de mai sus poate fi scrisa sub forma:
S daca S1 si S2 si Sn
si poate fi executata ca o procedura a unui limbaj de programare recursiv, unde S este antetul procedurii si S1, S2, Sn corpul acesteia. Deci, pe langa interpretarea declarativa, logica, a unei astfel de formule, aceasta poate fi interpretata procedural astfel: pentru a executa S se executa S1 si S2 si Sn.
In aceeasi perioada, A. Colmerauer si colectivul lui de cercetare de la Universitatea din Marsilia, au dezvoltat un limbaj de implementare a acestei abordari, pe care l‑au denumit Prolog, abreviere de la 'Programmation et Logique'. De atunci si pina in prezent, limbajul Prolog s‑a impus ca cel mai important limbaj de programare logica si s‑au dezvoltat numeroase implementari, atat ale unor interpretoare cat si ale unor compilatoare ale limbajului.
Limbajul Prolog este un limbaj declarativ, sustinut de o componenta procedurala. Spre deosebire de limbajele procedurale, cum ar fi C sau Java, in care rezolvarea problemei este specificata printr-o serie de pasi de executie sau actiuni, intr-un limbaj declarativ problema este specificata prin descrierea universului problemei si a relatiilor sau functiilor existente intre obiecte din acest univers. Exemple de astfel de limbaje sunt cele functionale, de exemplu Lisp, Scheme, ML, si cele logice, de exemplu Prolog.
Desi initial a fost gandit pentru scrierea programelor de prelucrare a limbajului natural, Prolog a devenit cu timpul, un limbaj de uz general, fiind o unealta importanta in aplicatiile de inteligenta artificiala. Anumite clase de probleme pot fi rezolvate mai usor in Prolog, decat in orice alt limbaj procedural. Pentru aceste probleme, un program Prolog poate avea de 10 ori mai putine linii decat echivalentul lui in C++ sau Java. Astfel de probleme sunt in principal cele dedicate prelucrarilor simbolice sau care necesita un proces de cautare a solutiei intr-un spatiu posibil de transformari ale problemei, in acest ultim caz structura de control implicit a masinii Prolog facilitand implementarea.
Prezentarea ce urmeaza a limbajului Prolog, este in principal orientata pe descrierea limbajului Prolog standard. Exemplele de programe din aceasta parte, cat si din partea a doua, sunt rulate utilizand interpretorul SWI-Prolog sub Windows, mediul de programare SWI-Prolog si particularitatile lui sintactice fiind prezentate in anexa.
1.1 Entitatile limbajului Prolog
Limbajul Prolog este un limbaj logic, descriptiv, care permite specificarea problemei de rezolvat, in termenii unor fapte cunoscute despre obiectele universului problemei si a relatiilor existente intre aceste obiecte. Executia unui program Prolog consta in deducerea implicatiilor acestor fapte si relatii, programul definind astfel o multime de consecinte ce reprezinta intelesul sau semnificatia declarativa a programului.
Un program Prolog contine urmatoarele entitati:
fapte despre obiecte si relatiile existente intre aceste obiecte;
reguli despre obiecte si relatiile dintre ele, care permit deducerea (inferarea) de noi fapte pe baza celor cunoscute;
intrebari, numite si scopuri, despre obiecte si relatiile dintre ele, la care programul raspunde pe baza faptelor si regulilor existente.
1.1.1 Fapte
Faptele sunt predicate de ordinul intai de aritate n, considerate adevarate. Ele stabilesc relatii intre obiectele universului problemei. Numarul de argumente ale faptelor este dat de aritatea (numarul de argumente) corespunzatoare a predicatelor.
Exemple
Fapt:
Aritate:
papagal(coco).
1
iubeste(mihai, maria).
2
iubeste(mihai, ana).
2
frumoasa(ana).
1
bun(gelu).
1
deplaseaza(cub, camera1, camera2).
3
Interpretarea particulara a predicatului si a argumentelor acestuia depinde de programator. Ordinea argumentelor, odata fixata, este importanta si trebuie pastrata la orice alta utilizare a faptului, cu aceeasi semnificatie. Multimea faptelor unui program Prolog formeaza baza de cunostinte Prolog. Se va vedea mai tarziu ca in baza de cunostinte a unui program Prolog sunt incluse si regulile Prolog.
1.1.2 Scopuri
Obtinerea consecintelor sau a rezultatului unui program Prolog se face prin fixarea unor scopuri, care pot fi adevarate sau false, in functie de continutul bazei de cunostinte Prolog. Scopurile sunt predicate, pentru care se doreste aflarea valorii de adevar in contextul faptelor existente in baza de cunostinte. Cum scopurile pot fi vazute ca intrebari, rezultatul unui program Prolog este raspunsul la o intrebare (sau la o conjunctie de intrebari). Acest raspuns poate fi afirmativ, yes, sau negativ, no. Se va vedea mai tarziu ca programul Prolog, in cazul unui raspuns afirmativ la o intrebare, poate furniza si alte informatii din baza de cunostinte.
Exemplu
Considerand baza de cunostinte specificata anterior, se pot pune diverse intrebari, cum ar fi:
?- iubeste(mihai, maria).
yes deoarece acest fapt exista in baza de cunostinte
?- papagal(coco).
yes
?- papagal(mihai).
no deoarece acest fapt nu exista in baza de cunostinte
?- inalt(gelu).
no
1.1.3 Variabile
In exemplele prezentate pana acum, argumentele faptelor si intrebarilor au fost obiecte particulare, numite si constante sau atomi simbolici. Predicatele Prolog, ca orice predicate in logica cu predicate de ordinul I, admit ca argumente si obiecte generice numite variabile. In Prolog, prin conventie, numele argumentelor variabile incepe cu litera, iar numele constantelor simbolice incepe cu litera mica. O variabila poate fi instantiata (legata), daca exista un obiect asociat acestei variabile, sau neinstantiata (libera), daca nu se stie inca ce obiect va desemna variabila.
La fixarea unui scop Prolog, care contine variabile, acestea sunt neinstantiate, iar sistemul incearca satisfacerea acestui scop, cautand printre faptele din baza de cunostinte un fapt, care se poate identifica cu scopul, printr‑o instantiere adecvata a variabilelor din scopul dat. Este vorba de fapt, de un proces de unificare a predicatului scop cu unul din predicatele fapte, existente in baza de cunostinte.
La incercarea de satisfacere a scopului, cautarea se face intotdeauna pornind de la inceputul bazei de cunostinte. Daca se intalneste un fapt, cu un simbol predicativ identic cu cel al scopului, variabilele din scop se instantiaza conform algoritmului de unificare si valorile variabilelor astfel obtinute sunt afisate, ca raspuns la satisfacerea acestui scop.
Exemple
?- papagal(CineEste).
CineEste = coco
?- deplaseaza(Ce, DeUnde, Unde).
Ce = cub, DeUnde = camera1, Unde = camera2
?- deplaseaza(Ce, Aici, Aici).
no
Cum se comporta sistemul Prolog in cazul in care exista mai multe fapte in baza de cunostinte care unifica cu intrebarea pusa In acest caz exista mai multe raspunsuri la intrebare, corespunzand mai multor solutii ale scopului fixat. Prima solutie este data de prima unificare si exista atatea solutii, cate unificari diferite exista. La realizarea primei unificari, se marcheaza faptul care a unificat si care reprezinta prima solutie. La obtinerea urmatoarei solutii, cautarea este reluata de la marcaj in jos, in baza de cunostinte. Obtinerea primei solutii este de obicei numita satisfacerea scopului, iar obtinerea altor solutii, resatisfacerea scopului. La satisfacera unui scop, cautarea se face intotdeauna de la inceputul bazei de cunostinte. La resatisfacerea unui scop, cautarea se face incepand de la marcajul stabilit de satisfacerea anterioara a acelui scop.
Sistemul Prolog, fiind un sistem interactiv, permite utilizatorului obtinerea fie a primului raspuns, fie a tuturor raspunsurilor. In cazul in care, dupa afisarea tuturor raspunsurilor, un scop nu mai poate fi resatisfacut, sistemul raspunde no.
Exemple
?- iubeste(mihai, X).
X = maria tastand caracterul ";" si Enter, cerem o noua solutie
X = ana
no
?- iubeste(Cine, PeCine).
Cine = mihai, PeCine = maria
Cine = mihai, PeCine = ana
no
Exista deci doua solutii pentru scopul iubeste(mihai, X) si tot doua solutii pentru scopul iubeste(Cine, PeCine), considerand tot baza de cunostinte prezentata in sectiunea 1.1.1.
1.1.4 Reguli
O regula Prolog exprima un fapt care depinde de alte fapte si este de forma:
S :- S1, S2, .Sn.
cu semnificatia prezentata la inceputul acestui capitol. Fiecare Si, i = 1,n si S au forma faptelor Prolog, deci sunt predicate, cu argumente constante, variabile sau structuri. Faptul S care defineste regula, se numeste antet de regula, iar S1, S2, .Sn formeaza corpul regulii si reprezinta conjunctia de scopuri, care trebuie satisfacute pentru ca antetul regulii sa fie satisfacut.
Fie urmatoarea baza de cunostinte Prolog:
frumoasa(ana). % 1
bun(vlad). % 2
cunoaste(vlad, maria). % 3
cunoaste(vlad, ana). % 4
iubeste(mihai, maria). % 5
iubeste(X, Y) :- % 6
bun(X),
cunoaste(X, Y),
frumoasa(Y).
Se observa ca enuntul (6) defineste o regula Prolog; relatia iubeste(Cine, PeCine), fiind definita atat printr-un fapt (5) cat si printr‑o regula (6).
In conditiile existentei regulilor in baza de cunostinte Prolog, satisfacerea unui scop se face printr‑un procedeu similar cu cel prezentat in Sectiunea 1.1.2, dar unificarea scopului se incearca atat cu fapte din baza de cunostinte, cat si cu antetul regulilor din baza. La unificarea unui scop cu antetul unei reguli, pentru a putea satisface acest scop trebuie satisfacuta regula. Aceasta revine la a satisface toate faptele din corpul regulii, deci conjunctia de scopuri.
Scopurile din corpul regulii devin subscopuri, a caror satisfacere se va incerca printr‑un mecanism similar cu cel al satisfacerii scopului initial.
Pentru baza de cunostinte descrisa mai sus, satisfacerea scopului
?- iubeste(vlad, ana).
se va face in urmatorul mod. Scopul unifica cu antetul regulii (6) si duce la instantierea variabilelor din regula (6): X = vlad si Y = ana. Pentru ca aceasta intrebare sa fie adevarata, trebuie indeplinita regula, deci fiecare subscop din corpul acesteia. Aceasta revine la indeplinirea scopurilor bun(vlad), care reuseste prin unificare cu faptul (2), cunoaste(vlad, ana), care reuseste prin unificare cu faptul (4), si a scopului frumoasa(ana), care reuseste prin unificare cu faptul (1). In consecinta, regula a fost indeplinita, deci si intrebarea initiala este adevarata, iar sistemul raspunde yes.
Ce se intimpla daca se pune intrebarea:
?- iubeste(X, Y).
Prima solutie a acestui scop este data de unificarea cu faptul (5), iar raspunsul este:
X = mihai, Y = maria
Sistemul
Prolog va pune un marcaj in dreptul faptului (5) care a
satisfacut
scopul. Urmatoarea
solutie
a scopului iubeste(X, Y) se obtine
incepand cautarea
de la acest marcaj in
continuare, in
baza de cunostinte.
Scopul unifica
cu antetul regulii (6) si
se vor fixa trei noi subscopuri de indeplinit, bun(X), cunoaste(X, Y)
si
frumoasa(Y). Scopul bun(X) este satisfacut de
faptul (2) si
variabila X este instantiata
cu valoarea vlad, ![]() . Se incearca
acum satisfacerea scopului cunoaste(vlad, Y),
care este satisfacut
de faptul (3) si
determina
instantierea
Y = maria. Se introduce in baza
de cunostinte un marcaj
asociat scopului cunoaste(vlad, Y),
care a fost satisfacut
de faptul (3).
. Se incearca
acum satisfacerea scopului cunoaste(vlad, Y),
care este satisfacut
de faptul (3) si
determina
instantierea
Y = maria. Se introduce in baza
de cunostinte un marcaj
asociat scopului cunoaste(vlad, Y),
care a fost satisfacut
de faptul (3).
Se incearca apoi satisfacerea scopului frumoasa(maria). Acesta esueaza In acest moment, sistemul intra intr‑un proces de backtracking, in care se incearca resatisfacerea scopului anterior satisfacut, cunoaste(vlad, Y), in speranta ca o noua solutie a acestui scop va putea satisface si scopul curent care a esuat, frumoasa(Y). Resatisfacerea scopului cunoaste(vlad, Y) se face pornind cautarea de la marcajul asociat scopului in jos, deci de la faptul (3) in jos. O noua solutie (resatisfacere) a scopului cunoaste(vlad, Y) este data de faptul (4), care determina instantierea Y = ana. In acest moment, se incearca satisfacerea scopului frumoasa(ana). Cum este vorba de un nou scop, cautarea se face de la inceputul bazei de cunostinte si scopul frumoasa(ana) este satisfacut de faptul (1). In consecinta a doua solutie a scopului iubeste(X, Y) este obtinuta si sistemul raspunde:
X = vlad, Y = ana
urmand un mecanism de backtracking, descris intuitiv in figura 1.1, prin prezentarea arborilor de deductie construiti de sistemul Prolog.
|
|
Figura 1.1. Mecanismul de satisfacere a scopurilor in Prolog
La incercarea de resatisfacere a scopului iubeste(X, Y), printr‑un mecanism similar, se observa ca nu mai exista alte solutii. In concluzie, fiind data baza de fapte si reguli Prolog anterioara, comportarea sistemului Prolog este:
?- iubeste(X, Y).
X = mihai, Y = maria
X = vlad, Y = ana
no
Observatii
La satisfacerea unei conjunctii de scopuri in Prolog, se incearca satisfacerea fiecarui scop pe rand, de la stanga la dreapta. Prima satisfacere a unui scop determina plasarea unui marcaj in baza de cunostinte in dreptul faptului sau regulii care a determinat satisfacerea scopului.
Daca un scop nu poate fi satisfacut (esueaza), sistemul Prolog se intoarce si incearca resatisfacerea scopului din stanga, pornind cautarea in baza de cunostinte de la marcaj in jos. Inainte de resatisfacerea unui scop, se elimina toate instantierile de variabile, determinate de ultima satisfacere a acestuia. Daca cel mai din stanga scop din conjunctia de scopuri nu poate fi satisfacut, intreaga conjunctie de scopuri esueaza
Aceasta comportare a sistemului Prolog, in care se incearca in mod repetat satisfacerea si resatisfacerea scopurilor din conjunctiile de scopuri defineste mecanismul de backtracking din Prolog.
In capitolul 4 se va discuta pe larg structura de control a sistemului Prolog, mecanismul fundamental de backtracking si modurile in care se poate modifica partial acest mecanism.
1.1.5 Un program Prolog simplu
Simplitatea si expresivitatea limbajului Prolog poate fi pusa in evidenta de urmatorul exemplu, care permite definirea rapida a unor relatii de asociere.
capitala(burundi,bujumbura).
capitala(bahamas,nassau).
capitala(africa_de_sud,pretoria).
capitala(canada,otawa).
capitala(chile,santiago).
capitala(elvetia,berna).
capitala(danemarca,copenhaga).
capitala(somalia,mogadiscio).
capitala(slovenia,ljubljana).
continent(burundi,africa).
continent(bahamas,america_de_nord).
continent(africa_de_sud,africa).
continent(canada,america_de_nord).
continent(chile,america_de_sud).
continent(elvetia,europa).
continent(danemarca,europa).
continent(somalia,africa).
continent(slovenia,europa).
capitala_continent(Oras,Cont):-capitala(Tara,Oras),continent(Tara,Cont).
Pentru intrebarea
capitala_continent(bujumbura,Cont).
Cont = africa.
sistemul Prolog indica continentul in care se afla capitala Bujumbura. De asemenea, se pot cere programului toate continentele asociate capitalelor indicate in baza de date Prolog astfel:
capitala_continent(Capitala,Cont).
Capitala = bujumbura
Cont = africa ;
Capitala = nassau
Cont = america_de_nord ;
Capitala = pretoria
Cont = africa ;
Capitala = otawa
Cont = america_de_nord ;
Capitala = santiago
Cont = america_de_sud ;
Capitala = berna
Cont = europa ;
Capitala = copenhaga
Cont = europa ;
Capitala = mogadiscio
Cont = africa ;
Capitala = ljubljana
Cont = europa ;
No
1.2 Sintaxa limbajului Prolog
Asa cum s‑a aratat in sectiunea anterioara, un program Prolog este format din fapte, reguli si intrebari, acestea fiind construite pe baza predicatelor definite de utilizator sau predefinite. In orice sistem Prolog, exista o multime de predicate predefinite, unele dintre acestea fiind predicate standard, iar altele depinzand de implementare. Argumentele predicatelor Prolog, prin analogie cu logica predicatelor de ordinul I, se numesc termeni, si pot fi constante, variabile sau structuri.
Clasificarea obiectelor in Prolog este prezentata in figura 1.2.
|
|
Figura 1.2. Clasificarea obiectelor in Prolog
1.2.1 Constante
Constantele definesc obiecte specifice, particulare, sau relatii particulare. Exista doua tipuri de constante: atomi si numere. Atomii sunt constante simbolice care incep, de obicei, cu o litera si pot contine litere, cifre si caracterul "_". Exista si alte caractere ce pot forma atomi speciali, care au o semnificatie aparte in limbaj. Atomii pot desemna:
obiecte constante care sunt argumentele predicatelor, de exemplu atomii mihai si maria in faptul iubeste(mihai, maria);
predicate Prolog, fie cele definite de utilizator, fie cele predefinite in sistem; de exemplu atomul iubeste in faptul iubeste(mihai, maria);
atomi speciali, de exemplu atomii ":-" si "?-" ;
diverse alte reguli de constructie sintactica a atomilor depind de implementare.
Numerele pot fi intregi sau reale; sintaxa particulara acceptata, cat si domeniile de definitie depinzand de implementare. Un numar intreg este un sir de cifre zecimale, eventual precedate de un semn. Exemple de numere intregi: 1 +23 1515 0 -97. Numerele reale depind de implementarea de Prolog. In general, ele sunt reprezentate intr‑o forma similara celor din limbaje gen Pascal, C, etc. Exemple de numere reale: 3.14 -0.0035 100.2 +12.02.
1.2.2 Variabile
Variabilele sunt, din punct de vedere sintactic, tot atomi, dar ele au o semnificatie speciala, asa cum s‑a aratat in Sectiunea 1.1.3. Spre deosebire de regulile generale admise pentru constructia atomilor, numele unei variabile poate incepe si cu simbolul "_", ceea ce indica o variabila anonima. Utilizarea unei variabile anonime semnifica faptul ca nu intereseaza valoarea la care se va instantia acea variabila
De exemplu, interogarea ?- iubeste( _, maria). semnifica faptul ca se intreaba daca exista cineva care o iubeste pe Maria, dar nu intereseaza cine anume. Limbajul Prolog face distinctia intre litere mari si litere mici (este case sensitive). Se reaminteste ca, din punctul de vedere al conventiei Prolog, numele oricarei variabile trebuie sa inceapa fie cu litera mare, fie cu "_".
In Prolog exista situatii in care o variabila apare o singura data intr‑o regula, caz in care nu avem nevoie de un nume pentru ea, deoarece nu este referita decat intr‑un singur loc. De exemplu, daca dorim sa scriem o regula care ne spune daca cineva este fiul cuiva, o solutie ar fi:
este_fiu(X) :- parinte(Z, X).
Se observa ca s-a denumit cu Z un parinte anonim. In acest caz, nu intereseaza cine apare pe post de parinte. Pentru a nu incarca regulile cu nume inutile, care pot distrage atentia si ingreuia citirea programelor, se pot considera astfel de variabile ca anonime, notate cu underscore "_". Deci regula anterioara se poate rescrie astfel:
este_fiu(X) :- parinte( _ , X).
Variabilele din Prolog nu sunt identice ca semnificatie cu variabilele Pascal sau C, fiind mai curand similare cu variabilele in sens matematic. O variabila, odata ce a primit o valoare, nu mai poate fi modificata. Acest lucru elimina efectele lateralet care sunt permise in limbajele procedurale. O variabila Prolog neinstantiata semnifica ceva necunoscut. Pentru structurile de date, care nu sunt variabile si care au nume, numele lor incepe cu minuscula, urmata de litere, cifre sau underscore.
Reprezentarea sirurilor depinde de implementarea Prolog. In SWI-Prolog, interpretor care se aliniaza la standardul Edinbourg Prolog, sirurile se reprezinta intre caractere '.
Exemple de siruri de caractere:
'Constantin Noica'
'<<-------->>'
Diferenta dintre siruri si atomi este urmatoarea: sirurile au o reprezentare interna mai relaxata si nu pot fi folosite pe post de atomi, in timp ce atomii au de obicei reprezentari interne consumatoare de memorie, in ideea ca ei trebuie regasiti rapid, cautarile Prolog facandu‑se in general dupa acesti atomi.
1.2.3 Structuri
O structura Prolog este un obiect ce desemneaza o colectie de obiecte corelate logic, care formeaza componentele structurii. Un exemplu este structura asociata obiectului carte, care este formata din componentele: titlu carte, autor, si an aparitie. Un fapt ce refera relatia de posedare a unei carti de Prolog de catre Mihai poate fi exprimat astfel:
poseda(mihai, carte(prolog, clocksin, 1997)).
unde carte(prolog, clocksin, 1997) este o structura cu numele carte si cu trei componente: prolog, clocksin si 1997. Se admit si structuri imbricate, de exemplu:
poseda(mihai, carte(prolog, autori(clocksin, mellish), 1997)).
unde predicatul poseda are doua argumente: primul argument este constanta mihai, iar cel de‑al doilea este structura carte(prolog .), cu doua componente, a doua componenta fiind structura autori(clocksin, mellish).
In Prolog, o structura se defineste prin specificarea:
(1) numelui structurii ( functorul structurii);
(2) elementelor structurii (componentele structurii).
Fie tipul punct(X, Y). Atunci tipul segment poate fi reprezentat ca segment(P1, P2). De exemplu, un segment, avand capetele in punctele (1, 1) si (2, 3), poate fi reprezentat astfel:
segment(punct(1, 1), punct(2, 3)).
Structurile Prolog pot fi utilizate pentru reprezentarea structurilor de date (liste, arbori). De exemplu, un arbore binar poate fi reprezentat in Prolog printr‑o structura cu functorul arb si trei componente: radacina, subarbore stang si subarbore drept. Astfel, structura
arb(barbu, arb(ada, vid, vid), vid)
reprezinta un arbore binar cu cheia din radacina barbu, cu subarborele drept vid si cu subarborele stang format dintr‑un singur nod cu cheia ada.
Exista si cazuri in care un obiect poate avea constituenti compusi de adancime variabila. Astfel se ajunge la al doilea tip de recursivitate in Prolog, si anume, recursivitatea obiectelor. De exemplu, un arbore binar, cu chei numerice poate fi definit astfel:
1) Nodul vid este un arbore; putem nota acest nod vid prin constanta nil;
2) Un nod frunza este un arbore, de exemplu nod(15, nil, nil);
3) Un nod cu succesor stang si succesor drept este un arbore, de exemplu nod(20, ArbStang, ArbDrept)
De exemplu, reprezentarea in Prolog a arborelui
|
|
este nod(1, nod(2, nod(4, nil, nil), nod(5, nod(7, nil, nil), nil)), nod(3, nil, nod(6, nil, nil)))
Observatii
Sintaxa structurilor este aceeasi cu cea a faptelor Prolog. Un predicat Prolog poate fi vazut ca o structura a carui functor este numele predicatului, iar argumentele acestuia reprezinta componentele structurii.
Considerarea predicatelor Prolog ca structuri prezinta un interes deosebit; atat datele cat si programele in Prolog au aceeasi forma, ceea ce faciliteaza tratarea uniforma si sinteza dinamica de programe. In capitolul 4 se vor prezenta predicate predefinite in Prolog, care permit sinteza si executia dinamica a programelor Prolog.
1.2.4 Operatori
Uneori este convenabil sa se scrie anumiti functori (nume de structuri sau predicate) in forma infixata. Aceasta este o forma sintactica ce mareste claritatea programului, cum ar fi cazul operatorilor aritmetici sau al operatorilor relationali.
Limbajul Prolog ofera o multime de operatori, unii care se regasesc in aproape orice implementare, iar altii care sunt specifici unei versiuni particulare de implementare a limbajului. In continuare se vor prezenta o parte dintre operatorii din prima categorie.
(1) Operatori aritmetici
Operatorii aritmetici binari, cum ar fi +, -, *, /, pot fi scrisi in Prolog in notatie infixata; de exemplu:
1 + 2*(X * Y) / Z
Aceasta sintaxa este de fapt o rescriere infixata a formei prefixate a structurilor echivalente:
+(1, / (* (2,*(X, Y)), Z))
Este important de retinut ca operatorii aritmetici sunt o rescriere infixata a unor structuri, deoarce valoarea expresiei astfel definita nu este calculata. Evaluarea expresiei se face la cerere, in cazul in care se foloseste operatorul predefinit infixat is, de exemplu:
X is 1 + 2.
va avea ca efect instantierea variabilei X la valoarea 3.
(2) Operatori relationali
Operatorii relationali sunt predicate predefinite infixate. Un astfel de operator este operatorul de egalitate =. Predicatul (operatorul) de egalitate X = Y reuseste daca X unifica cu Y. Din aceasta cauza, dandu‑se un scop de tipul X = Y, regulile de decizie care indica daca scopul se indeplineste sau nu sunt urmatoarele:
Daca X este variabila neinstantiata, iar Y este instantiata la orice obiect Prolog, atunci scopul reuseste. Ca efect lateral, X se va instantia la aceeasi valoare cu cea a lui Y. De exemplu:
carte(barbu, poezii) = X.
este un scop care reuseste si X se instantiaza la carte(barbu, poezii).
Daca atat X cat si Y sunt variabile neinstantiate, scopul X = Y reuseste, variabila X este legata la Y si reciproc. Aceasta inseamna ca ori de cate ori una dintre cele doua variabile se instantiaza la o anumita valoare, cealalta variabila se va instantia la aceeasi valoare.
Atomii si numerele sunt intotdeauna egali cu ei insisi.
Doua structuri sunt egale daca au acelasi functor, acelasi numar de componente si fiecare componenta dintr‑o structura este egala cu componenta corespunzatoare din cealalta structura. De exemplu, scopul:
autor(barbilian, ciclu(uvedenrode, poezie(riga_crypto))) =
autor(X, ciclu(uvedenrode, poezie(Y)))
este satisfacut, iar ca efect lateral se fac instantierile:
X = barbilian si Y = riga_crypto.
Operatorul de inegalitate = se defineste ca un predicat opus celui de egalitate. Scopul X = Y reuseste daca scopul X = Y nu este satisfacut si esueaza daca X = Y reuseste. In plus, exista predicatele relationale de inegalitate, definite prin operatorii infixati >, <, =<, >=, cu semnificatii evidente.
Un operator interesant este =:=. El face numai evaluare aritmetica si nici o instantiere. Exemplu:
1 + 2 =:= 2 + 1.
yes
1 + 2 = 2 + 1.
no
Predicatul = = testeaza echivalenta a doua variabile. El considera cele doua variabile egale doar daca ele sunt deja partajate. X = = Y reuseste ori de cate ori X = Y reuseste, dar reciproca este falsa
X = = X.
X=_23 %variabila neinstantiata
X= =Y.
no
X=Y, X= =Y.
X=_23, Y=_23 % X si Z variabile neinstantiate partajate
Comentariile dintr‑un program Prolog sunt precedate de caracterul "%".
Exemple
1. In cele mai multe implementari
Prolog exista
predefinit operatorul de obtinere a modulului unui numar,
mod. Presupunand ca
nu exista
operatorul predefinit mod, se poate
scrie un predicat Prolog cu efect similar. O definitie
posibila
a predicatului modulo(X, Y, Z),
cu semnificatia
argumentelor ![]() , presupunand X, Y > 0, este:
, presupunand X, Y > 0, este:
% modulo(X, Y, Z)
modulo(X, Y, X) :- X < Y.
modulo(X, Y, Z) :- X >= Y, X1 is X - Y, modulo(X1, Y, Z).
2. Plecand de la predicatul modulo definit anterior, se poate
defini predicatul de calcul al celui mai mare divizor comun a doua
numere, conform algoritmului lui Euclid, presupunand ![]() ,
, ![]() , astfel:
, astfel:
% cmmdc(X, Y, C)
cmmdc(X, 0, X).
cmmdc(X, Y, C) :- modulo(X, Y, Z), cmmdc(Y, Z, C).
La intrebarea
cmmdc(15, 25, C).
C=5
raspunsul sistemului este corect. In cazul in care
se incearca
obtinerea
unor noi solutii
(pentru semnificatia
cmmdc acest lucru este irelevant,
dar intereseaza
din punctul de vedere al functionarii
sistemului Prolog) se observa ca sistemul intra intr‑o
bucla
infinita,
datorita imposibilitatii resatisfacerii scopului modulo(X, Y, Z) pentru ![]() . Daca
la definitia
predicatului modulo se adauga
faptul:
. Daca
la definitia
predicatului modulo se adauga
faptul:
modulo(X, 0, X).
atunci predicatul modulo(X, Y, Z) va genera la fiecare resatisfacere aceeasi solutie, respectiv solutia corecta, la infinit. Cititorul este sfatuit sa traseze executia predicatului cmmdc in ambele variante de implementare a predicatului modulo.
3. Doi copii pot juca un meci intr‑un turneu de tenis daca au aceeasi varsta. Fie urmatorii copii si varstele lor:
copil(peter, 9).
copil(paul, 10).
copil(chris, 9).
copil(susan, 9).
Toate perechile de copii care pot juca un meci intr-un turneu de tenis sunt calculate de predicatul:
pot_juca(Pers1, Pers2) :-
copil(Pers1, Varsta), copil(Pers2, Varsta), Pers1 = Pers2.
4. Sa scriem un program care sa ii gaseasca Anei un partener la bal. Ea doreste sa mearga cu un barbat care este nefumator sau vegetarian. Pentru aceasta dispunem de o baza de date cu informatii despre cativa barbati:
barbat(gelu). barbat(bogdan). barbat(toma).
fumator(toma). fumator(dan).
vegetarian(gelu).
Pentru a exprima doleantele Anei, vom scrie doua reguli:
Ana se intalneste cu X daca X este barbat si nu este fumator.
Ana se intalneste cu X daca X este barbat si este vegetarian.
Adica:
ana_se_intalneste_cu(X) :- barbat(X), not(fumator(X)).
ana_se_intalneste_cu(X) :- barbat(X), vegetarian(X).
5. Un program Prolog este o insiruire de fapte (facts) si reguli (rules) care poarta denumirea de clauze (clauses). Faptele si regulile au o structura comuna, ceea ce permite sinteza dinamica de cod, care este adaugata in baza de cunostinte. Un fapt poate fi privit ca o regula care are ca premiza (ipoteza) scopul true, care este adevarat intotdeauna. Astfel:
fapt.
este echivalent cu
fapt :- true.
O regula fara antet, deci de forma:
scop.
determina executia automata a scopului scop la reconsultarea bufer‑ului in care apare. Efectul este similar cu cel obtinut la introducerea in fereastra principala a intrebarii:
scop.
Exemple de intrebari:
place(ellen, tennis). % lui ellen ii place tenisul
place(john, fotbal). % lui john ii place fotbalul
place(tom, baseball). % lui tom ii place baseball‑ul
place(eric, inot). % lui eric ii place inotul
place(mark, tenis). % lui mark ii place tenisul
place(bill, X) :- place(tom, X). % lui bill ii place ce ii place lui tom
% Ce sporturi ii plac lui john?
place(john, X).
X = fotbal
% Cui ii place tenisul?
place(Y, tenis).
Y = ellen;
Y = mark
% Putem pune si intrebari particulare:
place(ellen, tenis).
yes
place(ellen, fotbal).
no
place(bill, baseball).
yes
1.2.5 Liste
O lista este o structura de date ce reprezinta o secventa ordonata de zero sau mai multe elemente. O lista poate fi definita recursiv astfel:
(1) lista vida (lista cu 0 elemente) este o lista
(2) o lista este o structura cu doua componente: primul element din lista (capul listei) si restul listei (lista formata din urmatoarele elemente din lista).
Sfarsitul unei liste este de obicei reprezentat ca lista vida
In Prolog structura de lista este reprezentata printr‑o structura standard, predefinita, al carei functor este caracterul "." si are doua componente: primul element al listei si restul listei. Lista vida este reprezentata prin atomul special [ ]. De exemplu, o lista cu un singur element a se reprezinta in Prolog, prin notatie prefixata astfel .(a, [ ]), iar o lista cu trei elemene, a, b, c, se reprezinta ca: .(a, . (b, . (c, [ ]))).
Deoarece structura de lista este foarte des utilizata in Prolog, limbajul ofera o sintaxa alternativa pentru descrierea listelor, formata din elementele listei separate de virgula si incadrate de paranteze drepte. De exemplu, cele doua liste anterioare pot fi exprimate astfel:
[a]
[a, b, c]
Aceasta sintaxa a listelor este generala si valabila in orice implementare Prolog. O operatie frecventa asupra listelor este obtinerea primului element dintr‑o lista si a restului listei, deci a celor doua componente ale structurii de lista. Aceasta operatie este realizata in Prolog de operatorul de scindare a listelor "|" scris sub urmatoarea forma
[Prim | Rest]
Variabila Prim sta pe postul primului element din lista, iar variabila Rest pe postul listei care contine toate elementele din lista cu exceptia primului. Acest operator poate fi aplicat pe orice lista care contine cel putin un element. Daca lista contine exact un element, Rest va reprezenta lista vida Incercarea de identificare a structurii [Prim | Rest] cu o lista vida duce la esec. Mergand mai departe, se pot obtine chiar primele elemente ale listei si restul listei. Iata cateva echivalente:
[a, b, c] = [a | [b, c] ] = [a, b | [c] ] = [a, b, c | [ ] ] = [a | [b | [c] ] ] = [a | [b | [c | [ ] ] ] ].
In Prolog, elementele unei liste pot fi atomi, numere, liste si in general orice structuri. In consecinta se pot construi liste de liste.
Exemple
1. Se poate defini urmatoarea structura de lista
[carte(barbu, poezii), carte(clocksin, prolog)]
2. Considerand urmatoarele fapte existente in baza de cunostinte Prolog
pred([1, 2, 3, 4]).
pred([coco, sta, pe, [masa, alba]]).
se pot pune urmatoarele intrebari obtinand raspunsurile specificate:
?- pred([Prim | Rest]).
Prim = 1, Rest = [2, 3, 4];
Prim = coco, Rest = [sta, pe, [masa, alba]]
no
?- pred([ _, _ , _ , [ _ | Rest]])
Rest = [alba]
3. Un predicat util in multe aplicatii este cel care testeaza apartenenta unui element la o lista si care se defineste astfel:
% membru(Element, Lista)
membru(Element, [Element | _ ]).
membru(Element, [ _ | RestLista]) :- membru(Element, RestLista).
Functionarea acestui scurt program Prolog poate fi urmarita cerand raspunsul sistemului la urmatoarele scopuri:
?- membru(b, [a, b, c]). %1
yes
?- membru(X, [a, b, c]). %2
X = a
X = b
X = c
no
?- membru(b, [a, X, b]). %3
X = b
X = _G302
no
Deci pentru cazul in care primul argument este o variabila (%2), exista trei solutii posibile ale scopului membru(Element, Lista). Daca lista contine o variabila (%3), exista doua solutii pentru forma listei: [a, b, b], cand X se instantiaza la b si predicatul reuseste cu b membru pe a doua pozitie, si [a, _ , b], caz in care variabila X este neinstantiata - lucru marcat de sistem printr-un indentificator arbitrar de forma _G302 - si predicatul reuseste cu b membru pe a treia pozitie.
Observatii
Exemplul 3 pune in evidenta o facilitate deosebit de interesanta a limbajului Prolog, respectiv puterea generativa a limbajului. Predicatul membru poate fi utilizat atat pentru testarea apartenentei unui element la o lista, cat si pentru generarea, pe rand, a elementelor unei liste, prin resatisfacere succesiva In anumite contexte de utilizare, aceasta facilitate poate fi folositoare, iar in altele ea poate genera efecte nedorite atunci cand predicatul membru este utilizat in definirea altor predicate, asa cum se va arata in partea a doua a lucrarii.
La definirea unui predicat p, care va fi utilizat in definirea altor predicate, trebuie intotdeauna sa se analizeze numarul de solutii cat si solutiile posibile ale predicatului p. Acest lucru este necesar, deoarece daca p apare intr‑o conjunctie de scopuri p1,., pi‑1, p ,pi+1,., pn si unul dintre scopurile pi+1,., pn esueaza, mecanismul de backtracking din Prolog va incerca resatisfacerea scopului p. Numarul de solutii, precum si solutiile scopului p influenteaza astfel, in mod evident, numarul de solutii, cat si solutiile conjunctiei de scopuri p1,., pi‑1, p ,pi+1,., pn. Exemple in acest sens si modalitati de reducere a numarului total de solutii ale unui corp vor fi prezentate in capitolul 4.
1.3 Limbajul Prolog si logica cu predicate de ordinul intai
Limbajul Prolog este un limbaj de programare logica. Desi conceput initial pentru dezvoltarea unui interpretor de limbaj natural, limbajul s-a impus ca o solutie practica de construire a unui demonstrator automat de teoreme folosind rezolutia. Demonstrarea teoremelor prin metoda rezolutiei necesita ca axiomele si teorema sa fie exprimate in forma clauzala. Sintaxa si semantica limbajului Prolog permit utilizarea numai a unei anumite forme clauzale a formulelor bine formate: clauze Horn distincte. Se prezinta in continuare, pe scurt, notiunile logice de baza semnificative pentru limbajul Prolog.
1.3.1 Clauze Horn
Definitie Se numeste clauza o disjunctie de literali. Un literal este un predicat sau un predicat negat. Se numeste clauza Horn o clauza care contine cel mult un literal pozitiv.
Definitie Se numeste clauza vida o clauza fara nici un literal; clauza vida se noteaza, prin conventie, cu
Deoarece faptele si regulile Prolog sunt in forma clauzala, forma particulara a clauzelor fiind clauze Horn distincte, acestea din urma se mai numesc si clauze Prolog.
Definitie Se numeste clauza Horn o clauza care contine cel mult un literal pozitiv. O clauza Horn poate avea una din urmatoarele patru forme:
(1) o clauza unitara pozitiva formata dintr‑un singur literal pozitiv (literal nenegat);
(2) o clauza negativa formata numai din literali negati;
(3) o clauza formata dintr‑un literal pozitiv si cel putin un literal negativ, numita si clauza Horn mixta
(4) clauza vida
Definitie Se numeste clauza Horn distincta o clauza care are exact un literal pozitiv, ea fiind fie o clauza unitara pozitiva, fie o clauza Horn mixta
Clauzele Horn unitare pozitive se reprezinta in Prolog prin fapte, iar clauzele Horn mixte prin reguli. O clauza Horn mixta de forma:
S1 S2 Sn S
se exprima in Prolog prin regula:
S :- S1, S2, .Sn.
Semnificatia intuitiva a unei reguli Prolog are un corespondent clar in logica cu predicate de ordinul I daca se tine cont de faptul ca o clauza Horn mixta poate proveni din urmatoarea formula bine formata
S1 S2 Sn S
Variabilele din clauzele distincte se transforma in variabile Prolog, constantele din aceste formule in constante Prolog, iar functiile pot fi asimilate cu structuri Prolog. Deci argumentele unui predicat Prolog au forma termenilor din calculul cu predicate de ordinul I.
Exemple
1. Fie urmatoarele enunturi: Orice sportiv este puternic. Oricine este inteligent si puternic va reusi in viata. Oricine este puternic, va reusi in viata sau va ajunge bataus. Exista un sportiv inteligent. Gelu este sportiv. Exprimand enunturile in logica cu predicate de ordinul I se obtin urmatoarele formule bine formate:
A1. x) (sportiv(x) puternic(x))
A2. x) (inteligent(x) puternic(x) reuseste(x))
A3. x) (puternic(x) (reuseste(x) bataus(x)))
A4. x) (sportiv(x) inteligent(x))
A5. Sportiv(gelu)
Axiomele se transforma in forma clauzala si se obtin urmatoarele clauze:
C1. sportiv(x) puternic(x)
C2. inteligent(x) ~ puternic(x) reuseste(x)
C3. ~ puternic(x) reuseste(x) bataus(x)
C4. sportiv(a)
C4'. inteligent(a)
C5. sportiv(gelu)
Clauzele C1, C2, C4, C4' si C5 pot fi transformate in Prolog deoarece sunt clauze Horn distincte, dar clauza C3 nu poate fi transformata in Prolog. Programul Prolog care se obtine prin transformarea acestor clauze este urmatorul:
puternic(X) :- sportiv(X).
reuseste(X) :- inteligent(X), puternic(X).
sportiv(a).
inteligent(a).
sportiv(gelu).
2. Fie urmatoarele enunturi:
(a) Orice numar rational este un numar real.
(b) Exista un numar prim.
(c) Pentru
fiecare numar x exista
un numar y astfel incat
![]() .
.
Daca se noteaza cu prim(x) "x este numar prim", cu rational(x) "x este numar rational", cu real(x) "x este numar real" si cu mai_mic(x, y) "x este mai mic decat y", reprezentarea sub forma de formule bine formate in calculul cu predicate de ordinul I este urmatoarea:
A1. x) (rational(x) real(x))
A2. x) prim(x)
A3. x) ( y) mai_mic(x, y)
Reprezentarea in forma clauzala este:
C1. ~ rational(x) real(x)
C2. prim(a)
C3. mai_mic(x, mai_mare(x))
unde mai_mare(x) este functia Skolem care inlocuieste variabila y cuantificata existential. Forma Prolog echivalenta a acestor clauze este:
real(X) :- rational(X).
prim(a).
mai_mic(X, mai_mare(X)).
unde mai_mare(x) este o structura Prolog.
Este evident ca nu orice axioma poate fi transformata in Prolog si ca, dintr‑un anumit punct de vedere, puterea expresiva a limbajului este inferioara celei a logicii cu predicate de ordinul I. Pe de alta parte, limbajul Prolog ofera o multime de predicate de ordinul II, adica predicate care accepta ca argumente alte predicate Prolog, care nu sunt permise in logica cu predicate de ordinul I. Acest lucru ofera limbajului Prolog o putere de calcul superioara celei din logica clasica. Uneori, aceste predicate de ordinul II, existente in Prolog, pot fi folosite pentru a modela versiuni de programe Prolog, echivalente cu o multime de axiome, care nu au o reprezentare in clauze Horn distincte. Se propune cititorului, dupa parcurgerea sectiunii urmatoare, sa revina la Exemplul 1 si sa incerce gasirea unei forme Prolog relativ echivalente (cu un efect similar) cu clauza C3.
1.3.2 Respingere rezolutiva
Limbajul Prolog demonstreaza scopuri (teoreme) prin metoda respingerii rezolutive. Strategia rezolutiva utilizata in Prolog este strategia rezolutiei de intrare liniara. Aplicarea principiului rezolutiei in logica cu predicate de ordinul I, implica construirea rezolventului a doi literali complementari, care fie sunt identici, fie au fost facuti identici, prin aplicarea substitutiei, definita de cel mai general unificator al celor doi literali asupra clauzelor ce contin acesti doi literali.
Definitie Fie clauzele:
(C1 ![]()
(C2 ![]()
numite
clauze parinte si cel mai general unificator al literalilor Pi si Qj, cu ![]() . Atunci
. Atunci ![]() este un rezolvent binar al clauzelor C1 si C2
este un rezolvent binar al clauzelor C1 si C2
Observatie Rezolventul a doua clauze nu este unic. Aplicarea rezolutiei intre doua clauze care rezolva poate genera diversi rezolventi in cazul in care in cele doua clauze exista mai multi literali complementari care, prin unificare, pot fi facuti identici.
Demonstrarea teoremelor aplicand metoda respingerii prin rezolutie poate fi descrisa de algoritmul urmator. Enunturile care descriu problema trebuie exprimate in modelul logic si formeaza multimea de axiome A. Concluzia care trebuie obtinuta, deci rezolvarea problemei, este teorema de demonstrat.
Algoritm Respingerea prin rezolutie in logica cu predicate de ordinul I
1. Converteste setul de axiome A in forma clauzala si obtine multimea de clauze S0
2. Neaga teorema de demonstrat, transforma teorema
negata in forma clauzala si adauga rezultatul obtinut
la S0, ![]()
3. repeta
3.1. Selecteaza o pereche de clauze C1, C2
3.2. Fie literalii ![]() si
si ![]()
3.3. Aplica
unificarea si calculeaza ![]()
3.4. daca ![]()
atunci
3.4.1. Determina
![]()
3.4.2. daca ![]()
atunci ![]()
pana s-a obtinut clauza vida ( ) sau
nu mai exista nici o pereche de clauze care rezolva sau
o cantitate predefinita de efort a fost epuizata
4. daca s-a obtinut clauza vida
atunci teorema este adevarata (este demonstrata)
5. altfel
5.1. daca nu mai exista nici o pereche de clauze care rezolva
atunci teorema este falsa
5.2. altfel nu se poate spune nimic despre adevarul teoremei
sfarsit
Observatii
In cazul in care s-a obtinut clauza vida, metoda respingerii prin rezolutie garanteaza faptul ca teorema este adevarata, deci demonstrabila pe baza setului de axiome A.
Reciproc, daca teorema este adevarata, se poate obtine clauza vida, dupa un numar finit de executii ale pasului 3, cu conditia ca strategia de rezolutie sa fie completa.
Conditia de oprire a ciclului, 'o cantitate predefinita de efort a fost epuizata' a fost introdusa, deoarece metoda demonstrarii teoremelor prin respingere rezolutiva este semidecidabila in logica cu predicate de ordinul I. In cazul in care concluzia T de demonstrat este falsa, deci nu este teorema, este posibil sa se ajunga in situatia in care, daca avem noroc, 'nu mai exista nici o pereche de clauze care rezolva'. Atunci se poate concluziona ca teorema este falsa. Dar este de asemenea posibil ca pasul 3 sa se execute la infinit, daca T nu este teorema. Din acest motiv, se introduce o cantitate predefinita de efort (resurse de timp sau spatiu) la epuizarea careia algoritmul se opreste. In acest caz, s-ar putea ca teorema sa fie adevarata, dar efortul predefinit impus sa fie prea mic, sau se poate ca T sa nu fie teorema. Rezulta deci ca, nu se poate spune nimic despre adevarul teoremei.
Strategia rezolutiei liniare are la baza urmatoarea idee: orice rezolvent obtinut in rezolutie este utilizat ca unul din cei doi rezolventi pe baza carora se obtine urmatorul rezolvent. Astfel, daca S este multimea initiala de clauze, C0IS clauza de pornire, atunci:
C1
Ck+1 S}, k=1, 2, 3,.
Strategia rezolutiei de intrare liniara este un caz particular al strategiei rezolutiei liniare, in care una din clauzele care rezolva apartine intotdeauna setului initial de axiome. Astfel, daca S este multimea initiala de clauze, C0IS clauza de pornire, atunci:
C1
Ck+1 , k=1, 2, 3,.
Strategia rezolutiei liniare de intrare este o strategie rezolutiva foarte eficienta, dar nu este o strategie care, desi nu este completa in general, este completa pentru clauze Horn. Aceasta strategie este deosebit de eficienta din punct de vedere al implementarii si jutifica astfel forma restrictionata a clauzelor Prolog (clauze Horn).
1.4 Structura de control a limbajului Prolog
Spre deosebire de limbajele de programare clasice, in care programul defineste integral structura de control si fluxul de prelucrari de date, in Prolog exista un mecanism de control predefinit.
1.4.1 Seminificatia declarativa si procedurala
Semnificatia declarativa a unui program Prolog se refera la interpretarea strict logica a clauzelor acelui program, rezultatul programului fiind reprezentat de toate consecintele logice ale acestuia. Semnificatia declarativa determina daca un scop este adevarat (poate fi satisfacut) si, in acest caz, pentru ce instante de variabile este adevarat scopul. Se reaminteste ca o instanta a unei clauze este clauza de baza (clauza fara variabile) obtinuta prin instantierea variabilelor din clauza initiala In aceste conditii semnificatia declarativa a unui program Prolog se poate defini precum urmeaza
Definitie Un scop S este adevarat intr‑un program Prolog, adica poate fi satisfacut sau deriva logic din program, daca si numai daca
1. exista o clauza C a programului;
2. exista o instanta I a clauzei C astfel incat:
2.1. antetul lui I sa fie identic cu cel al lui S;
2.2. toate scopurile din corpul lui I sunt adevarate, deci pot fi satisfacute.
Observatii
In definitia de mai sus clauzele refera atat fapte, cat si reguli Prolog. Antetul unei clauze este antetul regulii, daca clauza este o regula Prolog (clauza Horn mixta si este chiar faptul, daca clauza este un fapt Prolog (clauza unitara pozitiva). Corpul unui fapt este considerat vid si un fapt este un scop, care se indeplineste intotdeauna.
In cazul in care intrebarea pusa sistemului Prolog este o conjunctie de scopuri, definitia anterioara se aplica fiecarui scop din conjunctie.
Semnificatia procedurala a unui program Prolog se refera la modul in care sistemul incearca satisfacerea scopurilor, deci la strategia de control utilizata. Diferenta dintre semnificatia declarativa si semnificatia procedurala este aceea ca cea de a doua defineste, pe langa relatiile logice specificate de program, si ordinea de satisfacere a scopurilor si subscopurilor. In prima sectiune a acestui capitol s‑a facut o prezentare informala a modalitatii procedurale de satisfacere a scopurilor in Prolog. In continuare, se rafineaza aceasta comportare. Din punct de vedere procedural, un program Prolog poate fi descris de schema bloc prezentata in figura 1.3.
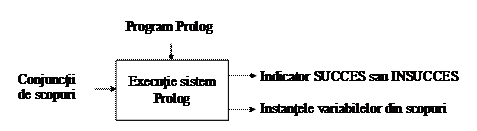
Figura 1.3. Comportarea procedurala a sistemului Prolog
Semnificatia procedurala a unui program Prolog poate fi descrisa de urmatorul algoritm, in care L = este lista de scopuri de satisfacut, iar B este lista de instantieri (unificari) ale variabilelor din scopuri, initial vida. Aceasta lista se va actualiza la fiecare apel.
Algoritm. Strategia de control Prolog
SATISFACE(L,B)
1. daca L = % lista vida
atunci afiseaza B si intoarce SUCCES.
2. Fie S1 primul scop din L si p predicatul referit de S1. Parcurge clauzele programului, de la prima clauza sau de la ultimul marcaj fixat, asociat lui p, pana ce se gaseste o clauza C al carei antet unifica cu S1.
3. daca nu exista o astfel de clauza
atunci intoarce INSUCCES.
4. Fie C de forma H :- D1,.,Dm, m 0 Plaseaza un marcaj in dreptul clauzei C, asociat lui p. (H contine predicatul p).
5. Redenumeste variabilele din C si obtine C' astfel incat sa nu existe nici o variabila comuna intre C' si L; C' este de tot forma H :- D1,.,Dm. cu redenumirile facute.
6. L % daca C este fapt, atunci L se va reduce
7. Fie B1 instantierea variabilelor care rezulta din unificarea lui S1 cu H.
8. Substituie variabilele din L' cu valorile date de B1 si obtine:
L
9. B B B1.
10. daca SATISFACE(L", B)=SUCCES
atunci afiseaza B si intoarce SUCCES.
11. repeta de la 1.
sfarsit
Observatii
Algoritmul de mai sus reprezinta de fapt implementarea strategiei rezolutive de intrare liniara utilizata de limbajul Prolog, pentru care se impune o ordine prestabilita de considerare a clauzelor.
Algoritmul arata functionarea sistemului pentru gasirea primei solutii.
Indicatorul SUCCES/INSUCCES corespunde raspunsurilor de yes, respectiv no, date de sistemul Prolog la incercarea de satisfacere a unei liste de scopuri.
1.4.2 Ordinea clauzelor si a scopurilor
Urmatoarele doua exemple pun in evidenta diferenta dintre semnificatia declarativa si semnificatia procedurala a programelor Prolog. Primul exemplu este un scurt program care defineste relatiile de parinte si stramos existente intre membrii unei familii. Se dau patru definitii posibile ale relatiei de stramos, str1, str2, str3 si str4, toate fiind perfect corecte din punct de vedere logic, deci din punct de vedere a semnificatiei declarative a limbajului.
% parinte(IndividX, IndividY)
% stramos(IndividX, IndividZ)
parinte(vali, gelu).
parinte(ada, gelu).
parinte(ada, mia).
parinte(gelu, lina).
parinte(gelu, misu).
parinte(misu, roco).
str1(X, Z) :- parinte(X, Z).
str1(X, Z) :- parinte(X, Y), str1(Y, Z).
% Se schimba ordinea regulilor:
str2(X, Z) :- parinte(X, Y), str2(Y, Z).
str2(X, Z) :- parinte(X, Z).
% Se schimba ordinea scopurilor in prima varianta
str3(X, Z) :- parinte(X, Z).
str3(X, Z) :- str3(X, Y), parinte(Y, Z).
% Se schimba atat ordinea regulilor, cat si ordinea scopurilor:
str4(X, Z) :- str4(X, Y), parinte(Y, Z).
str4(X, Z) :- parinte(X,Z).
|
|
Figura 1.4. Arborele genealogic definit de programul Prolog
Figura 1.4 prezinta arborele genealogic definit de faptele Prolog anterioare. In raport cu semantica declarativa a limbajului se pot schimba, fara a modifica intelesul logic, atat ordinea clauzelor care definesc relatia de stramos, cat si ordinea scopurilor in corpul regulii de aflare a stramosilor. Schimband ordinea clauzelor, se obtine din predicatul str1 definitia alternativa a relatiei de stramos str2; schimband ordinea scopurilor din corpul regulii in varianta initiala se obtine definitia predicatului str3; si, schimband atat ordinea clauzelor, cat si ordinea scopurilor in regula, se obtine predicatul str4.
Comportarea programului folosind cele patru definitii alternative, daca se doreste aflarea adevarului relatiei de stramos pentru perechile (ada, misu) si (mia, roco), este cea prezentata in continuare.
?- str1(ada, misu).
yes
Pentru acest scop, arborele de deductie este prezentat in figura 1.5.
|
|
Figura 1.5. Arborele de deductie a scopului str1(ada, misu)
?- str2(ada, misu).
yes
?- str3(ada, misu).
yes
Pentru scopul str3(ada, misu), arborele de deductie este cel prezentat in figura 1.6.
|
|
Figura 1.6. Arborele de deductie a scopului str3(ada, misu)
?- str4(ada, misu).
% bucla infinita; mesaj de depasire a stivei (ERROR: Out of local stack)
Pentru acest scop, arborele de deductie este cel prezentat in figura 1.7.
|
|
Figura 1.7. Arborele de deductie (infinit) a scopului str4(ada, misu)
Din punctul de vedere al semnificatiei procedurale, cele patru definitii nu sunt echivalente. Primele doua, str1 si str2, pot da raspuns pozitiv sau negativ la orice intrebare, dar str2 este mai ineficienta decat str1. Cititorul poate incerca trasarea arborelui de deductie al satisfacerii scopului str2(ada, misu) si compararea acestuia cu cel corespunzator satisfacerii scopului str1(ada, misu). Definitia str4 produce o bucla infinita datorita intrarii infinite in recursivitate. Este evident o definitie gresita din punct de vedere procedural. Definitia relatiei de stramos str3 este o definitie 'capcana'. Dupa cum se poate observa din arborele de deductie prezentat, raspunsul sistemului este afirmativ, in cazul in care exista o relatie de stramos intre cele doua persoane argumente ale predicatului. In cazul in care o astfel de relatie nu exista, sistemul intra intr-o bucla infinita, cum ar fi, de exemplu, pentru persoanele mia si roco.
?- str1(mia, roco).
no
?- str2(mia, roco).
no
?- str3(mia, roco).
% bucla infinita; mesaj de depasire a stivei
In acest caz, arborele de deductie al scopului str3(mia, roco) este prezentat in figura 1.8. Datorita semnificatiei procedurale a limbajului Prolog, trebuie urmarit cu atentie modul de definire a unui predicat, atat din punctul de vedere al ordinii clauzelor, cat si din punctul de vedere al ordinii scopurilor in corpul regulilor.
|
|
Figura 1.8. Arbore de deductie infinit pentru un scop fals
Al doilea exemplu se refera la rezolvarea in Prolog a urmatoarei probleme. O maimuta se gaseste la usa unei camere si o banana se afla agatata de plafon in centrul camerei. Langa fereastra camerei se afla o cutie pe care maimuta o poate folosi pentru a se urca pe ea si a ajunge la banana. Maimuta stie sa faca urmatoarele miscari: sa mearga pe sol, sa se urce pe cutie, sa deplaseze cutia daca este langa cutie, sa apuce banana daca este pe cutie si cutia este in centrul camerei. Se cere sa se scrie un program Prolog care sa descrie aceasta problema si care sa poata raspunde daca, dintr‑o configuratie initiala specificata prin pozitia maimutei si a cubului, maimuta poate apuca banana, dupa executia unei secvente de miscari.
Reprezentarea universului problemei in Prolog este specificata dupa cum urmeaza. Starea initiala este:
(1) Maimuta este la usa
(2) Maimuta este pe sol.
(3) Cutia este la fereastra
(4) Maimuta nu are banana.
si poate fi descrisa prin structura Prolog:
stare(la_usa, pe_sol, la_fereastra, nu_are_banana)
Starea finala este aceea in care maimuta are banana
stare( _ , _ , _ , are_banana)
Miscarile cunoscute de maimuta, deci operatorii de tranzitie dintr‑o stare in alta, sunt:
(m1) Apuca banana. apuca
(m2) Urca pe cutie. urca
(m3) Muta cutia. muta(Pozitia1, Pozitia2)
(m4) Merge (maimuta se deplaseaza pe sol). merge(Pozitia1, Pozitia2)
si sunt reprezentate prin structurile Prolog indicate la dreapta miscarilor.
Dintr‑o anumita stare numai anumite miscari sunt permise. De exemplu, maimuta nu poate apuca banana decat daca este urcata pe cutie si cutia este in centrul camerei, adica sub banana. Miscarile permise pot fi reprezentate in Prolog prin predicatul de deplasare depl cu trei argumente:
depl(Stare1, Miscare, Stare2)
|
|
care transforma problema din starea Stare1 in starea Stare2, prin efectuarea miscarii legale Miscare in starea Stare1. Se observa ca, reprezentarea aleasa este o reprezentare a problemei, folosind spatiul starilor.
Solutia problemei este completata prin adaugarea predicatului poatelua(Stare), care va reusi, daca maimuta poate ajunge din starea initiala Stare intr‑o stare finala, in care poate lua banana, stare finala descrisa de:
poate_lua(stare( _ , _ , _ , are_banana)).
Programul Prolog complet este prezentat in continuare.
% Structura stare:
% stare(poz_o_maimuta, poz_v_maimuta, poz_cub, are_nu_are_banana)
% Miscari admise: apuca, urca, muta(Pozitia1, Pozitia2),
% merge(Pozitia1, Pozitia2),
% reprezentate tot prin structuri.
% Predicate:
% depl(Stare1, Miscare, Stare2)
% poate_lua(Stare)
depl(stare(la_centru, pe_cutie, la_centru, nu_are_banana),
apuca, stare(la_centru, pe_cutie, la_centru, are_banana)).
depl(stare(P, pe_sol, P, H), urca, stare(P, pe_cutie, P, H)).
depl(stare(P1, pe_sol, P1, H), muta(P1, P2), stare(P2, pe_sol, P2, H)).
depl(stare(P1, pe_sol, B, H), merge(P1, P2), stare(P2, pe_sol, B, H)).
poate_lua(stare( _ , _ , _ , are_banana)).
poate_lua(Stare1) :- depl(Stare1, Miscare, Stare2), poate_lua(Stare2).
La intrebarea
?- poate_lua(stare(la_usa, pe_sol, la_fereastra, nu_are_banana)).
yes
sistemul raspunde afirmativ: maimuta este fericita si mananca banana.
O analiza atenta a programului conduce la concluzia ca programul da solutii numai pentru anumite situatii. In primul rand, strategia de control a miscarilor maimutei este impusa de ordinea clauzelor care definesc predicatul depl. Astfel, maimuta prefera intai sa apuce, apoi sa urce, apoi sa mute cubul si numai la urma sa mearga prin camera. Daca clauza corespunzatoare miscarii merge(Pozitia1, Pozitia2) ar fi fost pusa ca prima clauza in definitia predicatului de deplasare, maimuta ar fi mers la infinit prin camera, fara sa mai ajunga sa mute cubul sau sa apuce banana. Chiar pentru ordinea data a clauzelor, daca se pune intrebarea
?- poate_lua(stare(X, pe_sol, la_fereastra, nu_are_banana)).
Deci, daca intereseaza din ce pozitii maimuta poate lua banana, rezolvarea data nu este total satisfacatoare, deoarece programul are o infinitate de solutii. La cererea repetata a unei solutii, se va afisa intotdeauna valoarea:
X = la_fereastra
Considerand din nou modelul spatiului starilor, se observa ca in acest caz este vorba de un spatiu de cautare de tip graf, in care o aceeasi stare poate fi descoperita si redescoperita la infinit, prin parcurgerea unui ciclu de tranzitii de stari in acest graf. Astfel de cazuri trebuie tratate prin introducerea unor liste de stari parcurse, care sa impiedice parcurgerea repetata a unor stari deja parcurse.
Pericolul de aparitie a unor cicluri infinite, datorita parcurgerii unui spatiu de cautare graf nu este specific limbajului Prolog si poate sa apara in orice implementare, in aceste cazuri. Ceea ce este neobisnuit, in raport cu alte limbaje este faptul ca, semnificatia declarativa a programului este corecta, indiferent de ordonarea clauzelor, in timp ce programul este procedural incorect, avand comportari diferite in functie de aceasta ordonare. Rezolvarea problemei ar mai trebui completata cu afisarea starilor si a miscarilor executate de maimuta, pentru a ajunge in starea finala, in care ea poate apuca banana. Modalitati de eliminare a ciclurilor infinite, de tipul celor ce apar in aceasta problema, vor fi discutate in capitolele urmatoare.
1.5 Exercitii propuse
EP1. Exprimati in Prolog urmatoarele fapte:
1) susan are un cal;
2) rex mananca carne;
3) aurul este pretios;
4) masina este un Mercedes albastru cu capacitatea de cinci calatori.
EP2. Se considera urmatoarele fapte, exprimate in Prolog:
masina(mercedes, albastru, 5).
masina(chrysler, rosu, 4).
masina(ford, gri, 8).
masina(datsun, rosu, 5).
Sa se exprime urmatoarele intrebari in Prolog:
1) Ce tipuri de masini au cinci locuri pentru calatori?
2) Ce masini sunt rosii?
Sa se transcrie urmatoarea regula in Prolog:
X este o masina mare daca poate transporta cel putin 5 calatori.
EP3. Se da o baza de fapte de forma:
parinte(Parinte, Copil).
barbat(Persoana).
femeie(Persoana).
Se cere:
1) Sa se introduca cateva fapte de aceasta forma.
2) Sa se scrie regulile care definesc urmatoarele relatii de rudenie:
tata(Tata, Copil).
mama(Mama, Copil).
fiu(Parinte, Copil).
fiica(Parinte, Copil).
bunic(Bunic, Copil).
bunica(Bunica, Copil).
nepot(Bunic, Copil).
nepoata(Bunic, Copil).
3) Sa se puna urmatoarele intrebari:
Cine este parintele lui Dan?
Cine este fiu?
Cine este bunic?
Cine este fiu si tata?
EP4. Sa se descrie principalele operatii logice in Prolog: not, or, and, xor, nor, nand. Pentru aceasta se considera faptele
op_not(Variabila, Rezultat) si
op_or(Variabila1,Variabila2, Rezultat).
Sa se scrie:
1) faptele necesare descrierii lui op_not si op_or;
2) regulile necesare constructiei celorlalti operatori pe baza lui op_not si op_or. Se cer reguli pentru:
op_and(Var1, Var2, Rezultat).
op_xor(Var1, Var2, Rezultat).
op_nor(Var1, Var2, Rezultat).
op_nand(Var1, Var2, Rezultat).