
|
|
|
SISTEME CLASICE DE DESPECKLING
Aceasta categorie de filtre de despeckling este aplicata in domeniul spatial. Intre sistemele clasice de despeckling se afla urmatoarele filtre: Frost, Kuan si Lee. O comparatie a randamentului bazat pe utilizarea sub-imaginii Lena din mozaicul din figura 15, este prezentata in urmatorul tabel:
Zgomotos
Averager
7-1
Median
7-1
Lee
7-1
Kuan
9-1
Frost
5-1
3635
571.7
569.8
807.5
732.8
566
Tabel 1. O comparatie a randamentului unor sisteme clasice de despeckling
Randamentul a fost apreciat pe baza unei erori patratice medii estimate. Parametrii diferitelor filtre au fost selectati pentru a diminua eroarea patratica medie de iesire. Patratul primului parametru da dimensiunea ferestrei mobile folosite pentru estimarea deviatiei standard locale a componentei utile a imaginii de intrare, iar al doilea parametru, numarul echivalent de vederi ale imaginii de intrare. Am prezentat deja filtrul mediator si filtrul median. In cele ce urmeaza vom prezenta filtrele Frost, Kuan si Lee.
FILTRUL FROST
Este un filtru Weiner adaptat zgomotului multiplicativ, propus in lucrarea:
Frost, V. S., Stiles, J. A., Josephine, A., Shanmugan, K. S., and Holtzman, J. C., 1982. A Model for Radar Images and Its Application to Adaptive Digital Filtering of Multiplicative Noise. IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. PAMI-4, No. 2, March 1982.
Parametrii filtrului Frost sunt: dimensiunea ferestrei dreptunghiulare folosite pentru estimarea deviatiei standard locale a componentei utile a imaginii achizitionate (a se vedea documentul despre filtrul Wiener) si numarul sau de vederi (a se vedea documentul despre filtrul Speckle). Rezultatul procesarii imaginii lui Datcu in figura 15 cu un filtru Frost, este prezentat in figura 16.
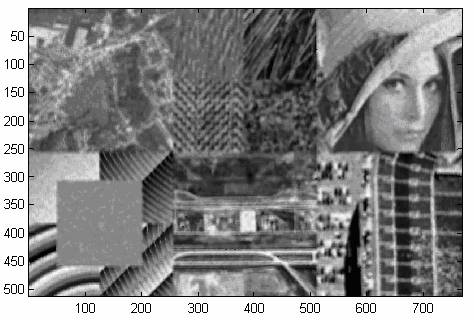
Figura 16. Imaginea din figura 15 avand un numar de vederi egal cu 1 tratata cu un filtru Frost folosind o fereastra mobila dreptunghiulara de dimensiunea 7x7.
FILTRUL KUAN
Kuan a considerat un model speckle multiplicativ si a proiectat un filtru liniar bazat pe criteriul erorii patratice medii minime (minimum mean square error MMSE), optim atunci cand atat scena cat si intensitatile detectate sunt distribuite de filtrul Gaussian. Mai multe despre acest filtru pot fi citite in urmatoarea referinta:
Kuan D. T., A.A. Sawchuk, T.C. Strand et al. Adaptive restoration of images with speckle. IEEE Trans. ASSP. 1987, Vol. 35, No. 3, 373-383.
Parametrii filtrului Kuan sunt: dimensiunea ferestrelor dreptunghiulare folosite pentru estimarea deviatiei standard locale a componentei utile a imaginii achizitionate (a se vedea documentul despre filtrul Wiener) si numarul sau de vederi (a se vedea documentul despre filtrul Speckle). Rezultatul procesarii imaginii lui Datcu din figura 15 cu un filtru Kuan este prezentat in figura 17.
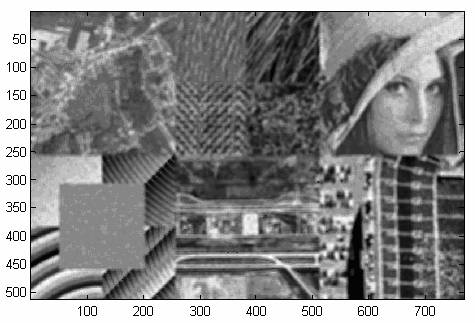
Figura 17. Imaginea din figura 15 avand un numar echivalent de vederi egal cu 1 tratat cu un filtru Kuan folosind o fereastra dreptunghiulara mobila de dimensiunea 7x7.
FILTRUL LEE
Filtrul Lee este un caz particular al filtrului Kuan datorat unei aproximatii liniare facute pentru un model de zgomot multiplicativ. A fost propus in lucrarea urmatoare:
Lee, J. S., 1981. Speckle Analysis and Smoothing of Synthetic Aperture Radar Images. Computer Graphics and Image Processing, Vol. 17: 24-32.
Parametrii filtrului Lee sunt: dimensiunea ferestrei dreptunghiulare folosite pentru estimarea deviatiei locale standard a componentei utile a imaginii achizitionate (a se vedea documentul despre filtrul Wiener) si numarul sau de vederi (a se vedea documentul despre filtrul Speckle). Rezultatul procesarii imaginii lui Datcu din figura 15 cu un filtru Lee este prezentat in figura 18.

Figura 18. Imaginea din figura 15 avand un numar echivalent de vederi egal cu 1 tratat cu un filtru Lee folosind o fereastra dreptunghiulara mobila de dimensiunea 7x7.
FILTRUL MAP
Filtrele Maximum A Posteriori (MAP) sunt de natura statistica, fiind bazate pe principiul lui Bayes. Deductia Bayesiana este aplicata pentru a elimina zgomotul speckle din imaginile SAR si SAS. In cazul zgomotului aditional:
![]()
(7)
unde y este o imagine zgomotoasa, x este o imagine fara zgomot si n zgomotul aditional, primul nivel al interferentei Bayesiene este dat de:
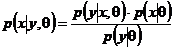
(8)
unde θ
reprezinta parametrul modelului, ![]() denota
functia densitate de probabilitate conditionala (pdf) a lui y dand lui x si asa-zisilor likelihood pdf,
denota
functia densitate de probabilitate conditionala (pdf) a lui y dand lui x si asa-zisilor likelihood pdf,
![]() denota prior
pdf, iar
denota prior
pdf, iar ![]() reprezinta evidence pdf. In (8),
reprezinta evidence pdf. In (8), ![]() pdf nu are rol in maximizarea lui x si, in consecinta,
estimatorul MAP este dat de urmatoarea ecuatie:
pdf nu are rol in maximizarea lui x si, in consecinta,
estimatorul MAP este dat de urmatoarea ecuatie:
![]()
(9)
unde pdf-urile likelihood si prior ar trebui definite. Estimatorul MAP este un estimator optimizat si minimizeaza valoarea functiei delta. De obicei, pdf-urile likelihood si prior sunt definite astfel incat ecuatia (9) sa devina:
![]()
(10)
unde px
reprezinta functia densitate de probabilitate (pdf) a lui x (prior pdf) si ![]() reprezinta pdf-ul
zgomotului (likelihood pdf). In
general, cea din urma ecuatie nu are o rezolvare analitica.
Exista cateva exceptii. Daca atat x cat si n sunt
distribuite Gaussian:
reprezinta pdf-ul
zgomotului (likelihood pdf). In
general, cea din urma ecuatie nu are o rezolvare analitica.
Exista cateva exceptii. Daca atat x cat si n sunt
distribuite Gaussian:
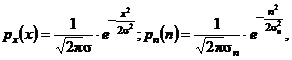
(11)
atunci filtrul MAP devine binecunoscutul filtru Wiener de ordin zero. Relatia sa de intrare-iesire (rezolvarea ecuatiei filtrului MAP) este:
![]()
(12)
Problema cu zgomotul speckle o reprezinta natura sa multiplicativa. Pentru a aplica un filtru MAP pentru despeckling, zgomotul multiplicativ trebuie transformat intr-un un zgomot aditional. Exista doua cai pentru aceasta transformare. Prima este bazata pe observatia ca o multiplicare poate fi produsa de completari repetate:
![]()
(13)
Cu notatiile:
![]()
(14)
relatia (13)
da forma relatiei (7), iar filtrul MAP poate fi aplicat imaginii
perturbate de zgomotul speckle. Cea de-a doua cale pe utilizarea logaritmului.
Calculand logaritmul imaginii ![]() produsul
produsul ![]() este transformat in
suma
este transformat in
suma ![]() . Cu notatiile
. Cu notatiile ![]() ,
, ![]() si
si ![]() prima ecuatie din relatia (13) este
transformata in relatia (7) iar filtrul MAP poate fi aplicat. Filtrul
nostru MAP este bazat pe prima metoda de transformare a zgomotului
multiplicativ in aditional si functioneaza cu ipotezele din
relatia (9). Rezultatul aplicarii sale in imaginea lui Datcu din
figura 15 este prezentat in figura 19.
prima ecuatie din relatia (13) este
transformata in relatia (7) iar filtrul MAP poate fi aplicat. Filtrul
nostru MAP este bazat pe prima metoda de transformare a zgomotului
multiplicativ in aditional si functioneaza cu ipotezele din
relatia (9). Rezultatul aplicarii sale in imaginea lui Datcu din
figura 15 este prezentat in figura 19.
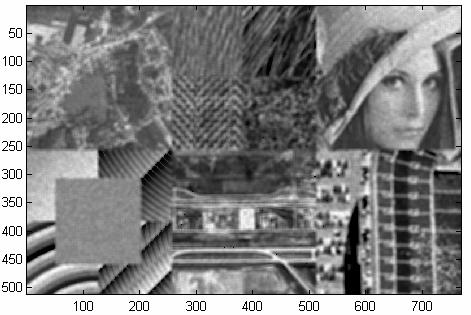
Figura 19. Imaginea din figura 15 avand un numar echivalent de vederi egal cu 1 tratata cu filtrul MAP.
FILTRUL EAP
Ca si filtrul MAP, filtrul Espected A Posteriori (EAP) este bazat pe principiul Bayes si incearca sa optimizeze estimarea a posteriori a imaginii SAR si SAS. Pot fi concepute doua tipuri de filtre recurente Bayes. Primul tip este bazat pe aplicarea unui filtru MAP la fiecare repetare iar cel de-al doilea este bazat pe utilizarea unui filtru EAP la fiecare repetare, asa cum poate fi observat in figura urmatoare.
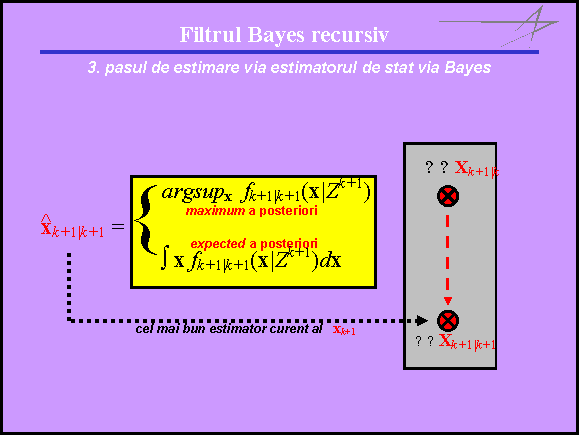
Figura 20. Doua solutii pentru constructia unui filtru recurent Bayes.
Astfel filtrul MAP maximizeaza probabilitatea a posteriori care reprezinta integrala pdf a variabilei aleatorii de iesire iar filtrul EAP maximizeaza alta integrala care reprezinta probabilitatea variabilei aleatorii de iesire. Rezultatul aplicarii filtrului EAP in imaginea din figura 15 este prezentat in figura 21.

Figura 21. Imaginea din figura 15 avand un numar echivalent de vederi egal cu 1 tratat cu un filtru EAP care foloseste o fereastra locala de dimensiunea 7x7.
FILTRUL CUANTIC
Cuantele sunt puncte aflate la intervale regulate din functia distributiva cumulativa a unei variabile aleatorie. Divizand datele ordonate in q subseturile esentiale de date de aceeasi dimensiune reprezinta motivatia pentru cuantele q; cuantele sunt valorile datelor care marcheaza limitele dintre subseturile consecutive. Altfel spus, kth cuanta q este valoarea x astfel incat probabilitatea ca o variabila aleatorie sa fie mai mica decat x este de maxim k/q iar probabilitatea ca o variabila aleatorie sa fie mai mare sau egala cu x este cel putin k/q. Exista cuante q − 1, cu k un numar intreg satisfacator 0 < k < q. Deseori, functia cuantelor poate fi preferata pentru orice impartire. Acest lucru este definit pentru variabilele existente intre zero si unu si, matematic, inversul functiei distributive cumulative.
Discutie
Daca o distributie este simetrica, atunci mediana este media (atata timp cat cea din urma exista). Dar, de obicei, mediana si media difera. De exemplu, cu o variabila aleatorie care are o distributie aleatorie (ca si variabila aleatorie care descrie o imagine SONAR, de exemplu) oricare exemplar particular al acestei variabile aleatorii va avea, in mare, o sansa de 63% de a fi mai mica decat media. Aceasta deoarece distributia exponentiala are o urma lunga de valori pozitive, dar este zero pentru numerele negative.
Cuantele sunt masuri utile deoarece ele sunt mai putin susceptibile distributiilor cu urma lunga (ca in cazul imaginilor SAR si SAS) si outliers.
In mod empiric, daca datele pe care le analizezi nu sunt, de fapt, distribuite conform distributiei presupuse de tine (cand aplicam un filtru Wiener am presupus ca imaginile SAR si SAS sunt distribuite Gaussian, dar imaginile SAR sunt distribuite Γ), sau daca ai alte potentiale surse pentru outliers care sunt indepartate de departe de medie, atunci cuantele pot fi mai utile statisticilor descriptive decat mediile si alte statistici asociate momentului (pentru filtrul Wiener am folosit media si variantele locale).
Destul de asemanator este subiectul deviatiei absolute least, o metoda de regresie (denoising, eliminarea zgomotului) care este mai robusta outliers-urilor decat cea a least squares (aplicate in cazul filtrului Wiener), unde suma valorii absolute a erorilor observate este folosita in locul erorii patratice. Legatura este ca media este estimarea singulara a distributiei care reduce eroarea least presupusa in timp ce mediana reduce eroarea absoluta presupusa. Deviatiile absolute least distribuie abilitatea de a fi relativ insensibile la deviatiile mari observatiile periferice, desi sunt disponibile si alte metode mai bune de regresie robusta.
Estimand cuantele
Exista mai multe metode pentru a estima cuantele prezentate in urmatoarele referinte:
Hyndman, R.J.; Fan, Y. (Noiembrie 1996). 'Sample Quantiles in Statistical Packages'. American Statistician 50 (4): 361-365. doi:10.2307/2684934.
Frohne, I.; Hyndman, R.J. (2008). Sample Quantiles. R Project. ISBN 3-900051-07-0
Filtrul cuantic
Filtrul median este un caz particular de filtru cuantic. Selectand cuantele care urmeaza celei de-a doua (cea care reprezinta mediana) alte filtre cuantice pot fi construite. In fiecare caz cuanta selectata este calculata local, utilizand o fereastra mobila, ca in cazul filtrului median. Rezultatul aplicarii filtrului cuantic in imaginea din figura 15 este prezentat in figura 22.

Figura 22. Imaginea din figura 15 avand un numar echivalent de vederi egal cu 1 tratata cu un filtru cuantic care utilizeaza o fereastra locala de dimensiunea 7x7.
FILTRUL LINIAR T
Filtrul liniar T marcheaza o transformare liniara a imaginii sale de intrare, X. Imaginea de iesire este exprimata de:
![]()
(15)
Transformarea liniara este utilizata pentru modificarea contrastului. Rezultatul aplicarii unui filtru liniar T in imaginea 15 este prezentat in figura 23.

Figura 22. Imaginea din figura 15 avand un numar echivalent de vederi egal cu 1 tratat cu un filtru Liniar T care utilizeaza o fereastra locala de dimensiunea 7x7.
WAVELETS
Toate metodele de filtrare prezentate deja au fost aplicate intr-un domeniu spatial. O alternativa este aplicarea filtrului in domeniul unei transformari. Rolul transformarii este obtinerea o mai buna reprezentare a imaginii achizitionate. De obicei, reprezentatie mai buna are o imprastiere mai mare apoi reprezentatia in domeniul spatial. Noua imagine are un numar mai redus de pixeli cu valori mari. Deci, filtrarea sa este mai simpla. Augmentarea imprastierii este realizata de necorelare. Exista unele produse ale transformarii ortogonale cu proprietati necorelate, ca in exemplul: produsul Discrete Karhunen-Loève (Discrete Karhunen-Loève Transform, DKLT), sau produsul Discrete Fourier (Discrete Fourier Transform, DFT), sau produsul Discrete Wavelet (Discrete Wavelet Transform, DWT).
DWT
Wavelet-urile, ψa,b(x), sunt functii generate de translatarea
si extinderea unei functii unice, numite mother wavelets, ψ(x): ![]() . Unele exemple de mother
wavelets sunt prezentate in figura 24.
. Unele exemple de mother
wavelets sunt prezentate in figura 24.
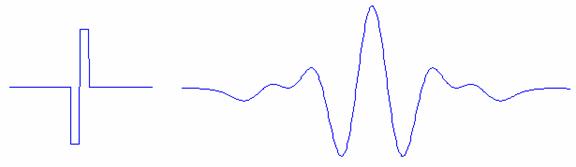
Figura24. Formele de unda ale wavelet-urilor propuse de Haar si Meyer.
Mother wavelet-urile lui Haar
au unele discontinuitati dar suportul sau este compact, iar mother wavelet-urile lui Meyer au un mai
mare grad de regularitate, dar suportul sau nu e compact. Ingrid Daubechies a propus prima familie de mother wavelet-uri cu suport compact si regularitate
impusa. Fiecarei mother
wavelet-uri ii corespunde o asa numita functie scalara,
![]() . Genereaza, prin translatii cu intregi, o
baza ortonormala a unui spatiu Hilbert
. Genereaza, prin translatii cu intregi, o
baza ortonormala a unui spatiu Hilbert ![]() . Utilizand astfel de baze, Mallat a definit o noua
structura matematica, analiza multirezolutie (a se vedea
Definitia 7.1, de la pagina 221 din Stéphane Mallat, A wavelet tour of
signal processing, Academic Press, 2001). Exista o colectie de
spatii Hilbert
. Utilizand astfel de baze, Mallat a definit o noua
structura matematica, analiza multirezolutie (a se vedea
Definitia 7.1, de la pagina 221 din Stéphane Mallat, A wavelet tour of
signal processing, Academic Press, 2001). Exista o colectie de
spatii Hilbert ![]() . Fiecare spatiu de acest gen, corespunde unei
rezolutii diferite (in functie de j)
si este generat de o baza ortonormala ale caror elemente
sunt obtinute din translatia cu intregi ale unei versiuni scalate a
unei functii de scalare
. Fiecare spatiu de acest gen, corespunde unei
rezolutii diferite (in functie de j)
si este generat de o baza ortonormala ale caror elemente
sunt obtinute din translatia cu intregi ale unei versiuni scalate a
unei functii de scalare ![]() . Cu ajutorul analizei
multirezolutie, poate fi definita o descompunere ortogonala
corespondenta. Fiecare element al descompunerii ortogonale,
. Cu ajutorul analizei
multirezolutie, poate fi definita o descompunere ortogonala
corespondenta. Fiecare element al descompunerii ortogonale, ![]() , poate fi exprimat ca diferenta dintre doua
elemente consecutive corespunzand analizei antirezolutie:
, poate fi exprimat ca diferenta dintre doua
elemente consecutive corespunzand analizei antirezolutie:
![]() . Fiecare spatiu Hilbert
. Fiecare spatiu Hilbert ![]() inchis este generat de
o baza ortogonala a caror elemente sunt obtinute prin
translatarea cu intregi a unei versiuni la scala a mother wavelets-urilor corespondente
inchis este generat de
o baza ortogonala a caror elemente sunt obtinute prin
translatarea cu intregi a unei versiuni la scala a mother wavelets-urilor corespondente ![]() . Cele doua concepte ale multi-rezolutiei si
descompunerii ortogonale sunt evidentiate in figura 25.
. Cele doua concepte ale multi-rezolutiei si
descompunerii ortogonale sunt evidentiate in figura 25.
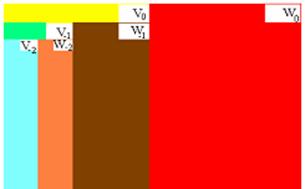
Figura 25. Un exemplu de asociere intre o analiza multirezolutie si corespondentul sau de descompunere ortogonala.
Spatiul ![]() este generat de
catre functia
este generat de
catre functia ![]() . Spatiul
. Spatiul ![]() , inclus in spatiul
, inclus in spatiul ![]() este generat de
catre functia
este generat de
catre functia ![]() , care poate fi exprimat in baza spatiului
, care poate fi exprimat in baza spatiului ![]() :
:
![]()
(16)
Spatiul ![]() , inclus in spatiul
, inclus in spatiul ![]() , este generat de catre functia
, este generat de catre functia ![]() , care poate fi exprimat in baza spatiului
, care poate fi exprimat in baza spatiului ![]() :
:
![]()
(17)
Secventele ![]() si
si ![]() reprezinta
raspunsurile la impuls a doua filtre in timp discret (primul de tip trece jos, iar cel de-al
doilea de tip trece sus) care poate fi folosit pentru a transforma baza
spatiului
reprezinta
raspunsurile la impuls a doua filtre in timp discret (primul de tip trece jos, iar cel de-al
doilea de tip trece sus) care poate fi folosit pentru a transforma baza
spatiului ![]() in bazele
spatiilor
in bazele
spatiilor ![]() si
si ![]() . Conexiunea dintre cele doua raspunsuri la impuls
este data de relatia:
. Conexiunea dintre cele doua raspunsuri la impuls
este data de relatia:
![]()
(18)
Sa
consideram un semnal apartinand spatiului Hilbert ![]() ,
, ![]() . Poate fi dezvoltat in baza acestui spatiu, folosind relatia:
. Poate fi dezvoltat in baza acestui spatiu, folosind relatia:
![]()
(19)
Proiectarea semnalului ![]() , pe spatiul
, pe spatiul ![]() este exprimata
prin:
este exprimata
prin:
![]()
(20)
Coeficientii
acestei descompuneri, ![]() , sunt numiti coeficienti de aproximatie.
Proiectarea semnalului
, sunt numiti coeficienti de aproximatie.
Proiectarea semnalului ![]() pe spatiul
pe spatiul ![]() este exprimata
prin:
este exprimata
prin:
![]()
(21)
Coeficientii
acestei descompuneri, ![]() , sunt numiti coeficienti de detaliu. Utilizand relatiile
(17) si (20) coeficientii
, sunt numiti coeficienti de detaliu. Utilizand relatiile
(17) si (20) coeficientii ![]() pot fi exprimati
cu ajutorul coeficientilor
pot fi exprimati
cu ajutorul coeficientilor ![]() . O relatie similara intre coeficientii
. O relatie similara intre coeficientii ![]() si
si ![]() poate fi
obtinuta folosind relatiile (16) si (21). Aceste
relatii reprezinta baza primei iteratii a algoritmului DWT,
reprezenta in figura 26.
poate fi
obtinuta folosind relatiile (16) si (21). Aceste
relatii reprezinta baza primei iteratii a algoritmului DWT,
reprezenta in figura 26.
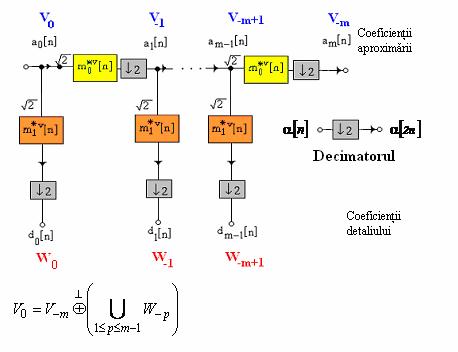
Figura 26. Implementarea DWT
a semnalului in timp discret ![]() .
.
DWT-ul semnalului ![]() este obtinut prin
concatenarea secventelor:
este obtinut prin
concatenarea secventelor: ![]() . DWT este inversabil. Inversa sa este numita
Transformata Wavelet Discreta Inversa Inverse Discrete Wavelet Transform, IDWT). Calcularea sa
este realizata folosind algoritmul prezentat in figura 27.
. DWT este inversabil. Inversa sa este numita
Transformata Wavelet Discreta Inversa Inverse Discrete Wavelet Transform, IDWT). Calcularea sa
este realizata folosind algoritmul prezentat in figura 27.
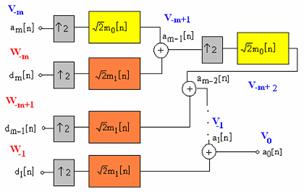
Figura 27. Implementarea
IDWT. Semnalul in timp discret ![]() este recuperat.
este recuperat.
Datorita raspandirii sale, DWT este des folosit in aplicatiile de procesare a semnalului digital. Exista doua aplicatii principale ale DWT, compresia si reducerea zgomotului. De fapt, Donoho a propus o metoda de reducere a zgomotului in domeniul DWT, pe care a numit-o eliminarea zgomotului. Toate metodele procesarii semnalului incluse in restul sectiunii SONARSCOPE sunt metode de eliminare a zgomotului. Metoda, originala a lui Donoho, de eliminare a zgomotului are trei pasi:
1) calcularea DWT a semnalului achizitionat (presupus a fi perturbat, in plus, cu un zgomot alb Gaussian);
2) filtrarea non-liniara a rezultatului obtinut;
3) calcularea IDWT a rezultatului obtinut.
Donoho a propus doua tipuri de filtre non-liniare: cu prag tare si prag moale:
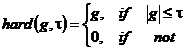
(22)
![]() unde
unde![]()
![]()
(23)
Pragul asociat cu aceste filtre (notate in ultimele doua relatii cu τ) este calculat luand in considerare variantele de zgomot. Donoho a propus, de asemenea, cativa estimatori ai variantelor zgomotului care pot fi aplicate semnalului achizitionat.
Algoritmul pentru calcularea DWT 2D este prezentat in figura 28.
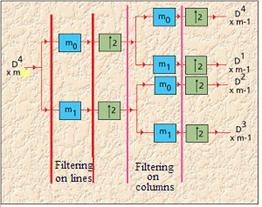
Figura 28. Implementarea unei iteratii DWT 2D.
Incepand
cu aproximarea sub-imaginii obtinute la iteratia anterioara, ![]() , si utilizand filtre de trece jos si trece sus pe linii si
coloane, asociate cu decimatori (cu factorul de decimare egal cu 2), sunt
obtinute patru sub-imagini noi:
, si utilizand filtre de trece jos si trece sus pe linii si
coloane, asociate cu decimatori (cu factorul de decimare egal cu 2), sunt
obtinute patru sub-imagini noi: ![]() . Luand in considerare faptul ca in acest caz sunt
implementate doua filtrari separate (pe linii si pe coloane)
sunt obtinute patru tipuri de rezultate: aproximatii, detalii
orizontale, detalii verticale si detalii diagonale. Organizarea acestor
rezultate este prezentata in figura urmatoare pentru cazul a trei
iteratii.
. Luand in considerare faptul ca in acest caz sunt
implementate doua filtrari separate (pe linii si pe coloane)
sunt obtinute patru tipuri de rezultate: aproximatii, detalii
orizontale, detalii verticale si detalii diagonale. Organizarea acestor
rezultate este prezentata in figura urmatoare pentru cazul a trei
iteratii.
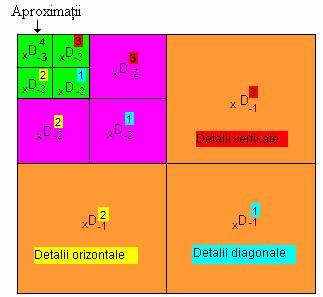
Figura 29. Rezultatul aplicarii unui DWT 2D calculat realizand 3 iteratii.
DESCOMPUNEREA WAVELETURILOR
In cele ce urmeaza, este prezentat un exemplu al aplicarii DWT 2D imaginii prezentate in figura 15.

Figura 30. Stanga - Imaginea originala, Dreapta - Rezultatul obtinut folosind DWT 2D cu 2 iteratii.
Analizand figura poate fi observat ca:
detaliul diagonal al sub-imaginii la primul nivel al descompunerii contine doar zgomot;
unele detalii orizontale ale componentei clare a imaginii originale pot fi observate in interiorul conturului galben in detaliile orizontale ale sub-imaginilor situate la primul si la cel de-al doilea nivel de descompunere;
unele detalii verticale ale componentei clare a imaginii originale pot fi observate in interiorul conturului rosu la al doilea nivel de descompunere.
zgomotul continut de sub-imaginea aproximata din cel de-al doilea nivel de descompunere este redus in comparatie cu zgomotul continut de imaginea originala.
Poate fi demonstrat ca daca imaginea originala este perturbata de un zgomot aditional alb Gaussian (additive white Gaussian noise, AWGN), cu o varianta specificata, atunci toate detaliile sub-imaginii sunt perturbate cu un AWGN, cu aceeasi varianta. Detaliile diagonale ale sub-imaginii din primul nivel de descompunere au cel mai mic continut de detalii ale componentei clare din imaginea originala. Acesta este motivul pentru care este utilizat la estimarea variantei de zgomot cerut pentru filtrarea non-liniara in al doilea pas a metodei de eliminare a zgomotului a lui Donoho. Aceasta estimare este realizata utilizand urmatorul estimator:
![]()
![]()
(24)
Va fi folosit in majoritatea functiilor SONARSCOPE urmatoare.
Urmarind localizarea contururilor galbene in figura 30, poate fi observata dependenta interscalara a DWT 2D. O variatie rapida in valorile coeficientului detaliului wavelet la un anumit nivel de descompunere poate fi gasita la urmatoarele niveluri de descompunere in aceeasi pozitie. Aceasta dependenta inter-scalara a coeficientilor detaliului wavelet poate fi exploatat in aplicatii de eliminare a zgomotului.
DWT are doi parametri:
mother wavelet-urile folosite (prin selectia functiei ψ, functia scalara corespondenta φ si raspunsurile la impuls corespondente m0 si m1 sunt selectate automat),
rezolutia primara (numar de iteratii).
Variind
acesti parametri pentru DWT a unui semnal dat, sunt obtinute
rezultate diferite. De exemplu,l imaginea Lena
a fost perturbata aditional cu zgomot alb de varianta ![]() si rezultatul a
fost eliminarea zgomotului folosind metoda lui Donoho. In domeniul wavelet a
fost folosit filtrul de prag tare. DWT a fost calculat folosind diferite mother
wavelets. Calitatea procedurii de eliminare a zgomotului poate fi
apreciata comparand ratia de zgomot a semnalului inalt (peak signal
to noise ratio, PSNR) a imaginii de iesire si a rezultatelor. O
astfel de comparatie este prezentata in tabelul urmator. In
cazul fiecarei mother wavelet valoarea pragului a fost selectata
pentru a maximiza corespondentul de iesire a PSNR.
si rezultatul a
fost eliminarea zgomotului folosind metoda lui Donoho. In domeniul wavelet a
fost folosit filtrul de prag tare. DWT a fost calculat folosind diferite mother
wavelets. Calitatea procedurii de eliminare a zgomotului poate fi
apreciata comparand ratia de zgomot a semnalului inalt (peak signal
to noise ratio, PSNR) a imaginii de iesire si a rezultatelor. O
astfel de comparatie este prezentata in tabelul urmator. In
cazul fiecarei mother wavelet valoarea pragului a fost selectata
pentru a maximiza corespondentul de iesire a PSNR.
PSNRs
![]()
input
D2
D3
D4
D5
D6
D7
D8
D9
D10
10
28.17
30.45
30.62
30.60
30.80
30.77
30.69
30.55
30.53
30.57
20
22.11
26.39
26.49
26.60
26.55
26.53
26.33
26.29
26.29
26.35
35
17.29
23.49
23.58
23.72
23.64
23.75
23.50
23.57
23.49
23.46
Tabelul 2. O comparatie a PSNR-urilor de iesire obtinute aplicand asociatia DWT - filtru de prag tare pentru diferite mother wavelet-uri folosite pentru calcularea DWT (cele noua mother wavelet-uri cu un suport compact propus de Daubechies, Dk - mother wavelet-urile care au k momente de pauza) a trei imagini obtinute perturband imaginea Lena cu AWGN avand varianta indicata pe prima coloana.
Pentru diferitele variante ale mother wavelet care maximizeaza PSNR-ul de iesire este diferita. Asadar mother wavelet-urile mai bune nu pot fi gasite pentru aplicatiile de eliminare a zgomotului imaginii. Pentru maximizarea PSNR de iesire trebuie executata o sinteza cu rezultat partial (ca cele prezente in tabelul 2).
TRANSFORMATA WAVELET DISCRETA CU DIVERSITATE MARITA (The Diversity Enhanced Discrete Wavelet Transform DEDWT
(Vechea denumire: Isar TODDE de prag moale)
Principiul acestei transformari este prezentat in urmatoarea figura.
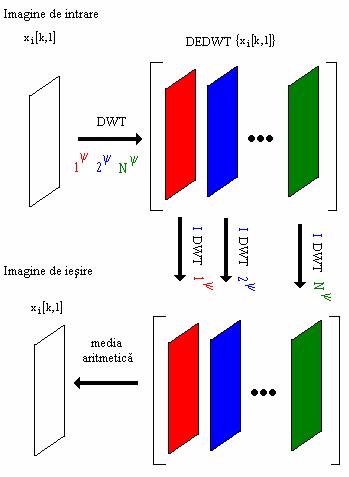
Figura 31. Principiul DEDWT.
Calculand DWT 2D al imaginii de intrare, folosind diferite mother wavelet-uri, este obtinuta o matrice, avand pe fiecare coloana diferite DWT 2D. Aceasta matrice reprezinta rezultatul aplicarii DEDWT 2D. Aplicand pe fiecare coloana corespondentul IDWT 2D (calculat folosind aceeasi mother wavelet) este obtinuta o noua matrice. Aceasta reprezinta rezultatul aplicarii Inversului Transformatei Wavelet Discreta cu Diversitate Marita 2D (2D Inverse Diversity Enhanced Discrete Wavelet Transform, 2D IDEDWT). Fiecare coloana a matricei contine imaginea de intrare. Facand media aritmetica a coloanelor, este obtinuta imaginea de iesire. Desigur, va fi identica cu imaginea de intrare. Aceasta noua transformare poate fi utilizata in aplicatiile de eliminare a zgomotului care implementeaza sistemul in figura 32.
Cu selectarea constantelor β de la iesirea egala cu 1/N, pentru N=9 si cu utilizarea filtrului de prag moale in domeniul wavelet-urilor pentru imaginea Lena perturbata cu AWGN cu varianta specificata, sunt obtinute rezultatele prezentate in urmatorul tabel.
Produsul DEDWT 2D este, in acest caz, un tabel de 3 din 1 dB. Aceasta metoda de eliminare a zgomotului poate fi utilizata, de asemenea, pentru tratarea imaginilor SAR si SAS. In cel din urma caz, arhitectura sistemului din figura 32 trebuie sa fie completata sub-sisteme pentru conversia zgomotului multiplicativ in zgomot aditional. Noul sistem de eliminare a zgomotului este prezentat in figura 33.
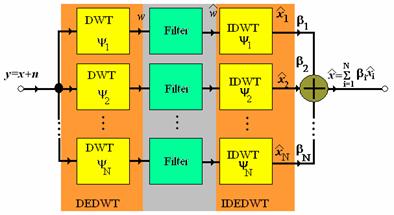
Figura 32. Un sistem de eliminare a zgomotului bazat pe utilizarea DEDWT.
![]()
D2
D3
D4
D5
D6
D7
D8
D9
D10
DEDWT
10
30.71
30.95
30.98
30.96
30.77
30.69
30.67
30.63
30.72
31.8
25
25.76
25.86
25.88
25.90
25.91
25.86
25.83
25.78
25.76
26.87
35
23.96
24.10
24.22
24.23
24.21
24.15
24.16
24.08
24.06
25.18
Tabelul 3. O comparatie intre randamentul 2D DEDWT si unele 2D DWTasociate cu un filtru de prag moale. Pragurile din fiecare caz au fost selectate pentru a maximiza PSNR de iesire.
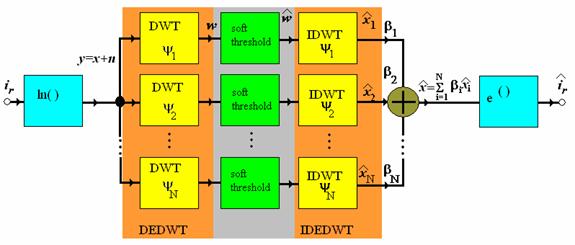
Figura 33. Arhitectura unui sistem de eliminare a zgomotului bazat pe utilizarea DEDWT 2D pentru procesarea imaginilor bruiate de un zgomot speckle.
Pentru N=9, cu selectarea constantelor β de la iesirea egala cu 1/N, rezultatul obtinut prin aplicarea sistemului in figura 34 imaginii din figura 15 este reprezentat in figura 34.

Figura 34. Iesirea sistemului din figura 33 cand la intrarea sa este aplicata imaginea din figura 15.
Functia lui SONARSCOPE are doua posibilitati pentru selectarea pragurilor din filtrele de prag moale din figura 33. Prima posibilitate, numita Automatic creeaza selectia valorii pragurilor proportionala cu varianta zgomotului n. Aceasta cantitate este estimata folosind relatia (24). A doua posibilitate este de a lasa operatorul sa selecteze manual valorile pragurilor. In acest caz, pentru fiecare valoare a pragului, operatorul este informat despre valoarea recomandata de sistem (valoarea folosita in procedura de selectie automata).
De fapt, filtrul de prag moale este un filtru MAP. Relatia sa de intrare-iesire este obtinuta rezolvand ecuatia (10) din urmatoarea repartitie:
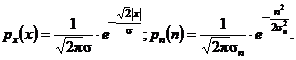
(25)
Cantitatea ![]() reprezinta
deviatia standard a imaginii
reprezinta
deviatia standard a imaginii ![]() in figura 34.
Repartitia acestei imagini este considerata de tip Laplacian. Pragul
τ in relatia (23) poate fi exprimat cu ajutorul deviatiei
standard a imaginii
in figura 34.
Repartitia acestei imagini este considerata de tip Laplacian. Pragul
τ in relatia (23) poate fi exprimat cu ajutorul deviatiei
standard a imaginii ![]() si a
variantei de zgomot
si a
variantei de zgomot ![]() utilizand
urmatoarea relatie:
utilizand
urmatoarea relatie:
![]()
(26)
Deci este proportional cu zgomotul variantei. In diviziunea Automatic a functiei SONARSCOPE aceasta constanta este selectata de catre cod. Deci valorile pragului sunt selectate global. Aceasta procedura poate fi imbunatatita prin estimarea locala a σ.
Selectarea pdf-ului imaginii ![]() in relatia (25)
este inspirata de catre histogramele detaliului coeficientilor
wavelet, care pot fi obtinute folosind functia SONARSCOPE,
DESCOMPUNEREA WAVELET. Pentru imaginea din figura 15, aceasta functie
readuce rezultatele reprezentate in urmatoarea figura.
in relatia (25)
este inspirata de catre histogramele detaliului coeficientilor
wavelet, care pot fi obtinute folosind functia SONARSCOPE,
DESCOMPUNEREA WAVELET. Pentru imaginea din figura 15, aceasta functie
readuce rezultatele reprezentate in urmatoarea figura.
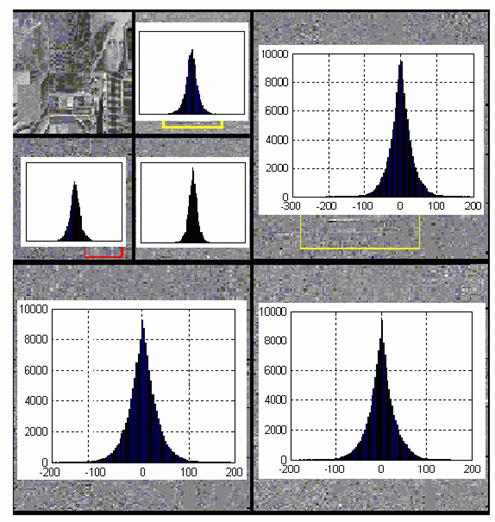
Figura 35. Histograma coeficientilor wavelet pentru experimentul descris in figura 31. Aceste distributii sunt de natura exponentiala (legea Laplaciana)
Distributia Laplaciana este de tip cu urma lunga. Filtrand imaginile zgomotoase care au distributia unei componente clare de tip cu urma lunga nu este o sarcina usoara. Asocierea DEDWT 2D - filtre de prag moale, are un randament bun de eliminare a zgomotului. Aceasta metoda de eliminare a zgomotului poate fi imbunatatita in baza urmatoarelor idei:
selectarea celui mai bun filtru, care ia in considerare dependenta inter-scalara a detaliului coeficientilor wavelet;
selectarea unui mai bun DWT.
DEDWT BISHRINK
(Vechea denumire: Isar TODDE bishrink V1)
Aceasta functie SONARSCOPE asociaza DEDWT 2D, deja introdusa cu filtrul bishrink, propus de Selesnik. Acest filtru MAP asta care ia in calcul dependenta inter-scalara a detaliului coeficientilor wavelet.
In cazul filtrului bishrink, zgomotul aditional presupus a fi distribuit Gaussian pentru componenta clara este considerata o distributie Laplaciana:
pn(![]() ,
,![]() )=
)=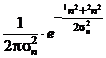
![]() si pwx=(
si pwx=(![]() ,
,![]() )=
)=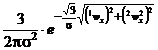
(27)
Rezultatul procesarii imaginii din figura 15 cu sistemul din figura 38 este prezentat in figura 38.
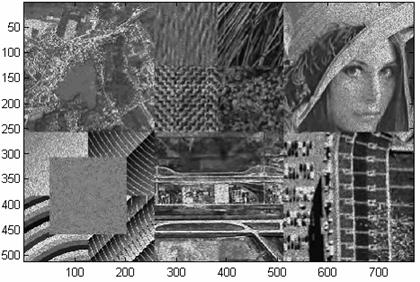
Figura 38. Rezultatul obtinut din aplicarea asocierii DEDWT - eliminarea zgomotului bishrink, imaginii din figura 15
DEDWT_BISHRINK_NSIG
(Vechea denumire: Isar TODDE - bishrink_nsig)
Functia SONARSCOPE este
asemanatoare cu cea a DEDWT_BISHRINK, deja prezentata. Exista
doar o diferenta intre aceste doua functii. In cazul noii
functii varianta de zgomot este estimata in fiecare sub-imagine
detaliu din primul nivel de descompunere, obtinand trei valori diferite
care corespund sub-bandelor orizontala, verticala si diagonala,
care sunt folosite la urmatoarele niveluri de descompunere pentru
sub-banda specifica in locul![]() Pentru estimarea variantei de zgomot, este
utilizat acelasi estimator pentru fiecare sub-banda:
Pentru estimarea variantei de zgomot, este
utilizat acelasi estimator pentru fiecare sub-banda:
![]()
(28)
Rezultatul obtinut prin tratarea imaginii din figura 15 cu aceasta noua functie (in versiune automata) este prezentat in figura 39. Cea de-a doua functie permite operatorului sa realizeze o selectie intre cele trei valori ale variantei de zgomot. Exista, de asemenea, posibilitatea de a trata logaritmul imaginii achizitionate.

Figura 39. Rezultatul obtinut aplicand functia DEDWT_bishrink_Nsig imaginii din figura 15.
DEDWT-BISHRINK-MIXED
(Vechea denumire: : Isar TODDE bishrink mix)
Filtrul bishrink are anumite drawbacks. Acesta este motivul pentru care este propusa urmatoarea varianta a filtrului. Realizeaza o estimare diferita a variantei locale a componentei clare a unei transformate wavelet a imaginii achizitionate si se comuta intre doua modele statistic diferite ale acestei componente dupa un anumit numar de iteratii ale transformatei wavelet.
Estimarea:
![]()
(29)
nu este foarte exacta. Este
bazata pe presupunerea corecta ca ![]() si
si ![]() sunt modelate ca
variabile aleatorii de medie zero. Dar restrictiile
vecinatatii finite N(k) nu sunt necesare variabilelor
aleatorii de medie zero. Deci este mai bine sa estimam mediile din
vecinatate, pentru inceput:
sunt modelate ca
variabile aleatorii de medie zero. Dar restrictiile
vecinatatii finite N(k) nu sunt necesare variabilelor
aleatorii de medie zero. Deci este mai bine sa estimam mediile din
vecinatate, pentru inceput:
![]()
(30)
iar mai apoi variantele:
![]()
(31)
Filtrul bishrink mixed se
aplica pentru primele doua iteratii ale DEDWT filtrul bishrink cu
estimare globala a variantei locale pentru estimarea lui ![]() si
si ![]() si apoi estimatorul
din relatia:
si apoi estimatorul
din relatia:
![]()
(32)
Rezultatul obtinut din tratamentul imaginii din figura 15 cu o functie SONAR noua este prezentat in figura 40.

Figura 40. Rezultatul obtinut din aplicarea functiei DEDWT_bishrink_mixed imaginii din figura 15.
DTCWT-BISHRINK-DIVERSITY-ENHANCED
(Vechea denumire: Isar (TOCAD - multibishrink))
Scopul crearii filtrelor liniare este bazat pe analizele sensibilitatii. In cazul filtrelor non-liniare acest tip de analiza poate fi generalizat. De exemplu, sensibilitatea unui filtru bishrink cu o estimare a zgomotului de deviatie standard poate fi calculata in relatia:
![]()
(33)
Relatia de intrare-iesire a filtrului bishrink poate fi pusa in urmatoarea forma:
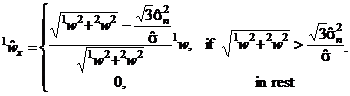
(34)
Derivativa estimarii cu estimarea zgomotului de deviatie standard devine:
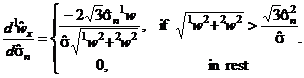
(35)
Imbunatatirea realizata prin metoda propusa creste o data cu cresterea variantei de zgomot.

Figura 41. O comparatie intre doua kernele: asocierea DTCWT - filtru bishrink (sus) si kernelul propus pentru eliminarea zgomotului (jos).
In sfarsit, rezultatul obtinut din aplicarea sistemului de despeckling DTCWT-BISHRINK-DIVERSITY-ENHANCED, imaginii din figura 15 este prezentat in figura 42.
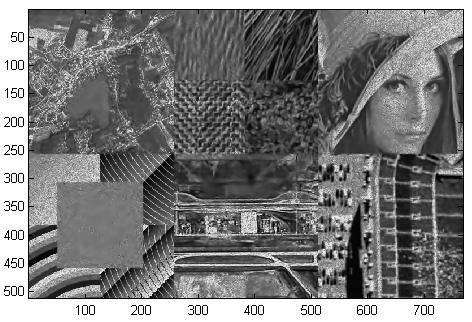
Figura 42. Rezultatul obtinut din aplicarea functiei DTCWT-BISHRINK-DIVERSITY-ENHANCED, imaginii din figura 15.