
|
|
|
Elementele fundamentale ale unei figuri geometrice sunt punctele topografice marcate pe teren prin tarusi sau cuie, fie pe aliniamente, fie pe figuri construite.
Fig. 28. Ridicarea unei perpendiculare cu ruleta
a) metoda numerelor pitagoreice b) metoda triunghiului isoscel
a) Ridicarea unei perpendiculare (Fig. 29) este operatia pe care o putem realiza cu ruleta intr-un punct oarecare de pe aliniament sau la una din extremitatile aliniamentului aplicand metoda triunghiului dreptunghic sau metoda triunghiului isoscel.
Metoda triunghiului dreptunghic bazata pe numerele pitagorice 3, 4, 5 sau multiplii de acestea, poate fi aplicata, atat de pe un punct oarecare al aliniamentului (Fig.29) cat si la extremitatea acestuia.
Fata de extremitatile punctelor C si D distantate la 3, 6, 9 . m unul de altul, cu ruleta si un instrument ascutit (fisa), vom descrie doua arce de cerc cu o lungime de 4, 8, 12 m din punctul C si respectiv 5, 10, 15 m din punctul D, care se intersecteaza in punctul P. Aliniamentul CP va fi perpendicular pe AB.
Metoda triunghiului isoscel (Fig. 29 b) aplicata de obicei dintr-un punct oarecare al aliniamentului, presupune a masura doua distante egale (CD = CE) pe aliniament, dupa care cu aceeasi deschidere a ruletei (ex.: DP=EP= 8m), vom trasa doua arce de cerc care se intersecteaza in punctul P. Aliniamentul CP va fi din nou perpendicular pe AB.
b) Coborarea unei perpendiculare (Fig. 30) Din punctul P, cu panglica sau ruleta se va descrie un arc de cerc, care va intersecta aliniamentul AB in punctele C si D. Se va masura distanta CD obtinuta, iar la jumatatea ei vom obtine punctul P' care reprezinta piciorul perpendicularei PP' pe aliniamentul AB.
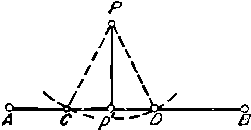
Fig. 30. Coborarea unei perpendiculare
c) Trasarea unui aliniament paralel la cel dat (Fig. 31)
Pe un aliniament AB se ia o lungime oarecare CD. In functie de distanta care se doreste a fi intre cele doua aliniamente se va masura in continuare aliniamentul CP, stabilind la jumatatea lui punctul 0. Din punctul D se masoara in continuare aliniamentul DO care se prelungeste cu OR (OD=OR). Aliniamentul nou obtinut RP va fi paralel cu AB.
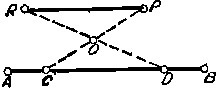
Fig. 31. Trasarea unui aliniament paralel la cel dat
d) Determinarea latimii unui curs de apa, ravena, rapa (Fig. 42). Din punctul A operatorul va cauta un semnal natural sau artificial pe malul opus, astfel incat aliniamentul AB sa fie aproximativ perpendicular pe cursul de apa. Pe aliniamentul AB se ridica o perpendiculara de lungime orizontala AC, iar in punctul C se ridica o alta perpendiculara CD astfel incat prin vizarea din D la B sa obtinem un punct de intersectie E a acestei vize cu aliniamentul AC.

Fig. 32. Determinarea distantei dintre 2 puncte aflate pe malurile unui rau
Pe teren se vor masura distantele orizontale AE; EC si CD, dus-intors cu panglica de otel etalonata.
Din asemanarea triunghiurilor AEB si CED rezulta:
![]()
e) Ridicarea in plan a unei suprafete de teren accesibila si cu vizibilitate utilizand panglica sau ruleta de otel
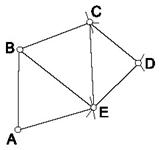
Dupa materializarea si
semnalizarea pe teren a punctelor caracteristice suprafetei ABCDE (Fig.
43), vom masura cu panglica sau ruleta toate laturile, precum si
diagonalele EB si EC care impart poligonul format in trei triunghiuri
oarecare.
Fig. 33.
Pentru transpunerea in plan toate lungimile masurate se vor reduce in prealabil la scara dupa care pe o dreapta oarecare se transpune latura AB. Din punctele A si B cu deschiderea in compas AE si BE se traseaza doua arce de cerc la intersectia carora se obtine punctul E. Se continua acest procedeu obtinand din punctele B si E punctul C, iar ultimul punct D se obtine din punctele C si E.
Suprafata poligonului masurat pe teren si transpus pe plan se obtine ca suma a suprafetelor celor trei triunghiuri, calculate fiecare in parte cu formula lui Heron.
![]()
in care: p (semiperimetrul)
![]() ;
;
a, b, c - laturile triunghiului.
f) Ridicarea in plan a unei suprafete de teren inaccesibila si fara vizibilitate in interior cu ruleta sau panglica de otel
In cazul unor astfel de suprafete (padure, plantatie de pomi sau vita, constructie), se masoara dus-intors toate laturile care unesc punctele caracteristice ale suprafetei si laturile unor mici triunghiuri isoscele de 510 m. (Fig. 34). Triunghiurile isoscele vom fi construite fie in interiorul fie in exteriorul suprafetei, in functie de accesibilitate si vizibilitatea oferite de teren.
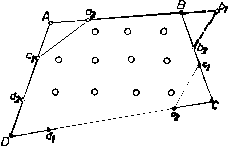
Fig. 34.
In vederea intocmirii planului topografic se vor
reduce la scara toate laturile patrulaterului, iar laturile triunghiurilor
isoscele vor fi reduse fie la aceeasi scara fie la una mai mare.
Rolul triunghiurilor isoscele este acela de a ne ajuta la trasarea
suprafetei pe plan prin intersectii de distante. Pe o
dreapta se va transpune la scara latura AB, iar pe prelungirea acesteia,
latura triunghiului isoscel Bb1. Cu deschiderea distantierului
Bb2 din punctul B si ![]() din
din ![]() vom construi doua
arce de cerc obtinand punctul
vom construi doua
arce de cerc obtinand punctul ![]() , care reprezinta directia laturii BC.
, care reprezinta directia laturii BC.
Pe aceasta directie vom transpune la scara punctul C, dupa care repetand operatiile si facand inchiderea grafica pe punctul initial se va obtine si pozitia punctului D (vezi Fig. 44).
Calculul suprafetei obtinute pe plan se va face prin metoda semigrafica impartind suprafata obtinuta in doua triunghiuri ale caror baze au fost masurate pe teren, iar inaltimile se vor lua grafic pe plan perpendicular pe baze. Verificarea calculului de suprafata se va face prin determinarea triunghiurilor din patrulater dupa cealalta diagonala.
g) Prelungirea unui aliniament dincolo de obstacol
Aceasta operatie o putem realiza prin doua procedee:
1) Prin ridicari de perpendiculare
2) Prin segmente proportionale
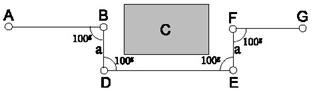
1. Procedeul perpendicularelor -
consta in ridicarea de segmente perpendiculare succesive pana la
depasirea obstacolului de pe directia aliniamentului (Fig. 35).
Fig. 35. Procedeul perpendicularelor
2. La realizarea prin segmente proportionale depasirea obstacolului pe teren se realizeaza cu ajutorul unui aliniament ajutator AY, prin ridicare si coborare de perpendiculare (Fig. 36).
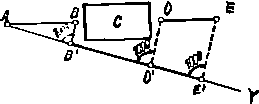
Fig. 36.
In faza initiala, dupa construirea aliniamentului AY sub un unghi convenabil fata de aliniamentul initial, care va permite trasarea aliniamentului pe langa obstacol, se va cobori o perpendiculara BB'. In continuare pe axa AY se vor alege convenabil punctele D' si E', pentru a putea ridica perpendiculare de pe ele dincolo de obstacol, avand lungimi deduse din relatia de asemanare a triunghiurilor ADD' si AEE' astfel:
![]() si
si ![]()
Punctele D si E trasate pe teren vor reprezenta prelungirea aliniamentului AB dincolo de obstacol.