
|
|
|
Gaurile negre nu sunt asa de negre
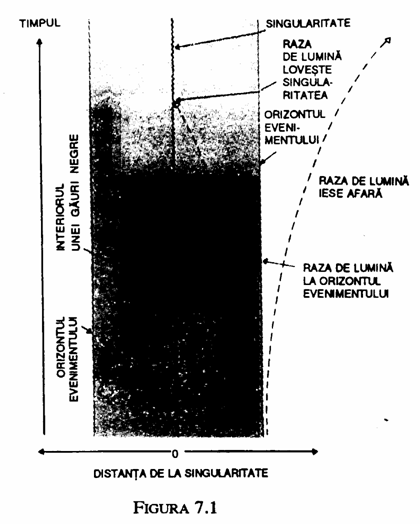
Inainte de 1970, cercetarea mea asupra relativitatii generalizate se concentra in principal asupra problemei daca existase sau nu o singularitate Big Bang. Totusi, intr-o seara de noiembrie a acelui an, la scurta vreme dupa nasterea fiicei mele, Lucy, pe cand ma duceam la culcare am inceput sa ma gandesc la gaurile negre. Invaliditatea mea face ca aceasta operatie sa fie un proces lent, astfel ca aveam destul timp. In acel timp nu exista o definitie precisa a punctelor din spatiu-timp care se gasesc in interiorul si in afara unei gauri negre. Discutasem deja cu Roger Penrose ideea de a defini o gaura neagra ca un set de evenimente din care nu era posibila iesirea la o distanta mare, definitie care acum este general acceptata. Ea inseamna ca limita gaurii negre, orizontul evenimentului, este formata din traiectoriile in spatiu-timp ale razelor de lumina care nu mai pot iesi din gaura neagra, ramanand pentru totdeauna la marginea ei (fig. 7.1). Este cam ca atunci cand fugiti de politie si reusiti sa pastrati doar un pas inaintea ei, dar nu puteti sa scapati definitiv!
Odata am realizat ca traiectoriile acestor raze de lumina nu s-ar putea apropia niciodata una de alta. Daca s-ar apropia, ele ar trebui in cele din urma sa intre una in alta. Ar fi ca si cand ati intalni pe cineva care fuge de polipe in directie opusa ati fi prinsi amandoi! (Sau, in acest caz, ar cadea intr-o gaura neagra.) Dar, daca aceste raze de lumina ar fi inghitite de gaura neagra, atunci ele nu ar fi putut fi la limita gaurii negre. Astfel, traiectoriile razelor de lumina in orizontul evenimentului trebuie sa fie intotdeauna paralele sau divergente una fata de alta. Un alt mod de a vedea aceasta este ca orizontul evenimentului, limita gaurii negre, este marginea unei umbre umbra unui sfarsit iminent. Daca priviti umbra facuta de o sursa aflata la mare distanta, cum este soarele, veti vedea ca razele de lumina de la margine nu se apropie unele de altele.
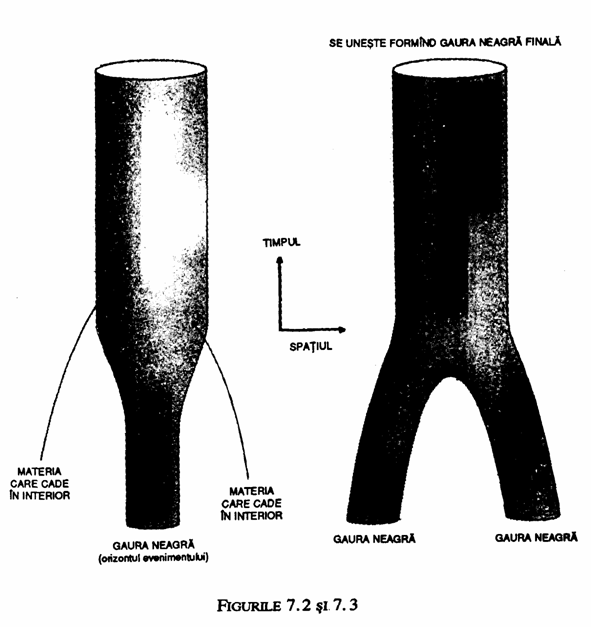
Daca razele de lumina care formeaza orizontul evenimentului, limita gaurii negre, nu se pot apropia niciodata una de alta, aria orizontului evenimentului poate ramane aceeasi sau se poate mari cu timpul dar nu se poate micsora niciodata deoarece aceasta ar insemna ca cel putin unele dintre razele de lumina de la limita ar trebui sa se apropie una de alta. De fapt, aria ar creste ori de cate ori in gaura neagra ar cadea materie sau radiatie (fig. 7.2). Or, daca doua gauri negre s-ar ciocni si s-ar uni formand o singura gaura neagra, orizontul evenimentului gaurii negre finale ar fi mai mare decat sau egal cu suma ariilor orizonturilor evenimentului gaurilor negre initiale (fig. 7.3). Aceasta proprietate de a nu se micsora a ariei orizontului evenimentului a introdus o restrictie importanta asupra comportarii posibile a gaurilor negre. Am fost atat de surescitat de descoperirea mea ca nu am prea dormit in noaptea aceea. A doua zi l-am sunat pe Roger Penrose. El a fost de acord cu mine. Cred, de fapt, ca el isi daduse seama de aceasta proprietate a ariei. Totusi, el folosise o definitie usor diferita a unei gauri negre. El nu realizase ca limitele unei gauri negre, conform celor doua definitii, ar fi aceleasi si deci la fel ar fi si arii1e lor, cu conditia ca gaura neagra sa se stabilizeze la o stare care nu se modifica in timp.
Comportarea fara micsorare a ariei unei gauri negre amintea foarte mult de comportarea unei marimi fizice numita entropie, care masoara gradul de dezordine al unui sistem. Se stie din experienta ca dezordinea tinde sa creasca daca lucrurile sunt lasate in voia lor. (Cineva trebuie numai sa inceteze de a mai face reparatii in jurul casei pentru a vedea aceasta!) Se poate crea ordine din dezordine (de exemplu, se poate zugravi casa) dar aceasta necesita cheltuirea unui efort sau a unei energii si astfel scade cantitatea disponibila de energie ordonata.
O enuntare exacta a acestei idei este a doua lege a termodinamicii. Ea afirma ca entropia unui sistem izolat creste intotdeauna si ca atunci cand se unesc doua sisteme, entropia sistemului combinat este mai mare decat suma entropiilor sistemelor individuale. De exemplu, sa consideram un sistem de molecule de gaz dintr-o cutie. Moleculele pot fi considerate ca mici bile de biliard care se ciocnesc incontinuu una de alta si de peretii cutiei. Cu cat este mai mare temperatura gazului, cu atat se misca mai repede moleculele gazului si cu atat mai frecvent si mai tare se vor ciocni cu peretii cutiei, cu atat mai mare va fi presiunea exercitata de ele asupra peretilor. Sa presupunem ca initial toate moleculele sunt limitate printr-un perete la partea stanga a cutiei. Daca apoi peretele se scoate, moleculele vor tinde sa se imprastie si sa ocupe ambele jumatati ale cutiei. La un anumit moment ulterior ele ar putea, datorita intamplarii, sa se gaseasca toate in jumatatea dreapta sau inapoi in jumatatea stanga, dar este mult mai probabil ca vor exista numere aproximativ egale in cele doua jumatati. O astfel de stare este mai putin ordonata, sau mai dezordonata decat starea initiala in care toate moleculele erau intr-o jumatate de cutie. Prin urmare, se spune ca entropia gazului a crescut. In mod asemanator, sa presupunem ca se incepe cu doua cutii, una care contine molecule de oxigen si cealalta cu molecule de azot. Daca se unesc cutiile si se elimina peretele intermediar, moleculele de oxigen si de azot vor incepe sa se amestece. La un moment ulterior cea mai probabila stare ar fi un amestec destul de uniform de molecule de oxigen si azot in ambele cutii. Aceasta stare ar fi mai putin ordonata si deci ar avea o entropie mai mare decat starea initiala a celor doua cutii separate.
A doua lege a termodinamicii are un statut diferit de acela al celorlalte legi ale stiintei, cum este legea gravitatiei a lui Newton, de exemplu, deoarece ea nu este valabila intotdeauna, doar in marea majoritate a cazurilor. Probabilitatea ca toate moleculele de gaz din prima noastra cutie sa se gaseasca intr-o jumatate de cutie la un moment ulterior este de unu la multe milioane de milioane, dar acest lucru se poate intampla. Totusi, daca cineva are o gaura neagra in apropiere, pare a fi un mod mai usor de a incalca legea a doua: trebuie numai sa se arunce in gaura neagra materie cu entropie mare, cum ar fi o cutie cu gaz. Entropia totala a materiei din afara gaurii negre ar scadea. Desigur, se poate inca spune ca entropia totala, inclusiv entropia din interiorul gaurii negre, nu a scazut dar, deoarece nu se poate privi in interiorul gaurii negre, nu putem spune cat de multa entropie are materia din interior. Deci, ar fi bine daca ar exista o caracteristica a gaurii negre prin care observatorii din afara gaurii negre sa poate spune care este entropia sa, si care ar creste ori de cate ori in gaura neagra cade materie care transporta entropie. Ca urmare a descoperirii descrise mai sus, ca aria orizontului evenimentelor creste atunci cand in gaura neagra cade materie, un student in cercetare de la Princeton numit Jacob Bekenstein a sugerat ca aria orizontului evenimentelor era o masura a entropiei gaurii negre. Atunci cand in gaura neagra cade materie care transporta entropie, aria orizontului sau va creste, astfel ca suma entropiilor materiei din afara gaurii negre si a ariei orizonturilor nu s-ar micsora niciodata.
Aceasta ipoteza parea sa impiedice incalcarea legii a doua a termodinamicii in majoritatea situatiilor. Totusi, avea un defect fatal. Daca o gaura neagra are entropie, atunci ea trebuie sa aiba si temperatura. Dar un corp cu o anumita temperatura trebuie sa emita radiatii cu o anumita rata. Este un lucru bine cunoscut ca daca cineva incalzite un vatrai in foc el straluceste incandescent si emite radiatii, dar si corpurile cu temperaturi mai scazute emit radiatii; acest lucru nu se observa in mod normal, deoarece cantitatea lor este destul de mica. Aceasta radiatie este necesara pentru a preveni incalcarea legii a doua. Astfel, gaurile negre trebuie sa emita radiatii. Dar chiar prin definitie, se presupune ca gaurile negre sunt obiecte care nu emit nimic. Prin urmare se pare ca aria orizontului evenimentelor unei gauri negre nu poate fi privita ca entropia sa. In 1972 am scris o lucrare cu Brandon Carter si un coleg american, Jim Bardeen, in care am aratat ca desi erau foarte multe asemanari intre entropie si aria orizontului evenimentului, exista aceasta dificultate aparent fatala. Trebuie sa admit ca am scris aceasta lucrare in parte datorita faptului ca eram iritat de
Bekenstein care, simteam, utilizase in mod gresit descoperirea mea privind cresterea ariei orizontului evenimentului. Totusi, in cele din urma a reiesit ca el era esentialmente corect, desi intr-un mod la care desigur nu se astepta.
In septembrie 1973, in timp ce vizitam Moscova, am discutat despre gaurile negre cu doi experti sovietici Jakov Zeldovici si Alexandr Starobinsky. Ei m-au convins ca, in conformitate cu principiul de incertitudine din mecanica cuantica, corpurile negre rotitoare trebuie sa creeze si sa emita particule. Am crezut argumentele lor din punct de vedere fizic, dar nu mi-a placut modul matematic in care au calculat emisia. Prin urmare, am inceput sa elaborez o tratare matematica mai buna, pe care am descris-o la un seminar tinut la Oxford la sfarsitul lui noiembrie 1973. In acel moment nu facusem calculele pentru a afla cat de mult s-ar emite in realitate. Ma asteptam sa descopar doar radiatia gaurilor negre rotitoare pe care Zeldovici si Starobinsky o prezisesera. Totusi, cand am facut calculul, am descoperit, spre surpriza si iritarea mea, ca si gaurile negre nerotitoare ar trebui aparent sa creeze si sa emita particule cu o rata stationara. La inceput am crezut ca aceasta emisie arata ca una din aproximatiile pe care le-am utilizat nu era valabila. Mi-era teama ca daca Bekenstein afla aceasta, ar putea sa o utilizeze ca un argument suplimentar pentru a-si sustine ideile privind entropia gaurilor negre, care mie tot nu-mi placea. Totusi, cu cat ma gandeam mai mult la ea, cu atat mai mult parea ca aproximatiile ar trebui sa fie valabile intr-adevar. Dar ceea ce m-a convins in cele din urma ca emisia era reala a fost faptul ca spectrul particulelor emise era exact acela care ar fi fost emise un corp fierbinte si ca gaura neagra emitea particule cu exact rata corecta pentru a impiedica incalcarea legii a doua. De atunci calculele au fost repetate in mai multe forme de alte persoane. Toate confirma ca o gaura neagra trebuie sa emita particule si radiatie ca si cand ar fi un corp fierbinte cu o temperatura care depinde numai de masa gaurii negre: cu cat este masa mai mare, cu atat este mai scazuta temperatura.
Cum este posibil sa rezulte ca o gaura neagra emite particule cand noi stim ca nimic nu poate scapa din orizontul evenimentului sau? Teoria cuantica ne da raspunsul: particulele nu vin din gaura neagra, ci din spatiul gol care se afla imediat in afara orizontului gaurii negre! Putem intelege acest lucru in felul urmator: Ceea ce noi consideram un spatiu "gol" nu poate fi complet gol deoarece aceasta ar insemna ca toate campurile, cum sunt campurile gravitational si electromagnetic, ar trebui sa fie exact zero. Totusi, valoarea unui camp si rata sa de modificare in timp sunt ca pozitia si viteza unei particule: principiul de incertitudine arata ca, cu cat se cunoaste mai precis una din aceste cantitati, cu atat mai putin precis se poate cunoaste cealalta. Astfel, in spatiul liber campul nu poate fi exact zero, deoarece atunci el ar trebui sa aiba atat o valoare precisa (zero), cat si o rata de modificare precisa (zero). In valoarea campului trebuie sa existe o valoare minima a incertitudinii sau fluctuatiei cuantice. Se pot considera aceste fluctuatii ca perechi de particule de lumina sau gravitatie care apar impreuna in acelasi timp, se departeaza si apoi se unesc din nou si se anihileaza reciproc. Aceste particule sunt particule virtuale ca particulele care transporta forta gravitationala a soarelui: spre deosebire de particulele reale, ele nu pot fi observate direct cu un detector de particule. Totusi, efectele lor indirecte, cum sunt modificari mici ale energiei orbitelor electronilor din atomi, se pot masura si concorda cu prezicerile teoretice cu un grad de precizie remarcabil. Principiul de incertitudine mai prezice ca vor exista perechi virtuale similare de particule de materie cum sunt electronii si quarcii. In acest caz insa, un membru al perechii va fi o particula si celalalt o antiparticula (antiparticulele de lumina si gravitatie sunt aceleasi ca particulele).
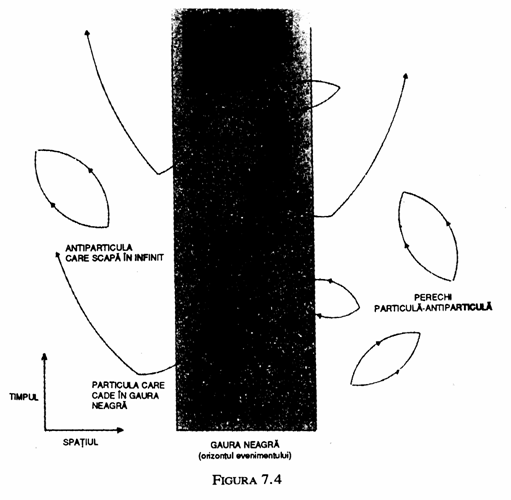
Deoarece energia nu poate fi creata din nimic, unu1 din partenerii dintr-o pereche particula/antiparticula va avea energie pozitiva si celalalt partener energie negativa. Cel cu energie negativa este condamnat sa fie o particula virtuala de viata scurta, deoarece in situatii normale particulele reale au intotdeauna energie pozitiva. Prin urmare trebuie sa-si caute partenerul si sa se anihileze reciproc. Totusi, o particula reala in apropierea unui corp masiv are mai putina energie decat daca s-ar afla la mare distanta, deoarece ar fi nevoie de energie pentru a ridica-o la distanta impotriva atractiei gravitationale a corpului. In mod normal, energia particulei este inca pozitiva, dar campul gravitational din interiorul unei gauri negre este atat de puternic incat chiar o particula reala poate avea acolo energie negativa. Prin urmare, este posibil, in prezenta unei gauri negre, ca particula virtuala cu energie negativa sa cada in gaura neagra si sa devina o particula sau antiparticula reala. In acest caz ea nu mai trebuie sa se anihileze cu partenerul sau. si partenerul sau abandonat poate cadea in gaura neagra. Sau, avand energie pozitiva, el poate scapa din vecinatatea gaurii negre ca o particula sau antiparticula reala (fig. 7.4). Pentru un observator aflat la distanta, el va parea ca a fost emis din gaura neagra. Cu cat este mai mica gaura neagra, cu atat este mai scurta distanta pe care particula cu energie negativa va trebui sa o parcurga inainte de a deveni o particula reala si astfel cu atat va fi mai mare rata de emisie si temperatura aparenta a gaurii negre.
Energia pozitiva a radiatiei energetice ar fi echilibrata de o curgere a particulelor de energie negativa in gaura neagra. Prin ecuatia lui Einstein E = mc2 (unde E este energia, m este masa si c este viteza luminii), energia este proportionala cu masa. Prin urmare, o curgere a energiei negative in gaura neagra reduce masa sa. Deoarece gaura neagra pierde masa, aria orizontului evenimentului devine mai mica, dar aceasta descrestere a entropiei gaurii negre este mai mult decat compensata de entropia radiatiei emise, astfel ca legea a doua nu este incalcata niciodata.
O gaura neagra cu masa de cateva ori mai mare decat masa soarelui ar avea o temperatura de numai o zecime de milionime de grad peste zero absolut. Aceasta este mult mai mica decat temperatura radiatiilor de microunde care umplu universul (circa 2,7° peste zero absolut), astfel ca gaurile negre ar emite chiar mai putin decat absorb. Daca universul este destinat sa se extinda mereu, temperatura radiatiilor de microunde va descreste in cele din urma pana la mai putin decat aceea a unei gauri negre de acest fel, care va incepe sa piarda masa. Dar, chiar si atunci, temperatura sa ar fi atat de scazuta incat ar trebui un milion de milioane de milioane de milioane de milioane de milioane de milioane de milioane de milioane de milioane de milioane de ani (1 urmat de saizeci si sase de zerouri) pentru a se evapora complet. Acesta este un timp mult mai mare decat varsta universului, care este de numai zece sau douazeci de miliarde de ani (1 sau 2 urmat de zece zerouri). Pe de alta parte, asa cum s-a mentionat in capitolul 6, puteau exista gauri negre primordiale cu masa mult mai mica decat daca s-ar fi format prin colapsul neregularitatilor din etapele foarte timpurii ale universului. Astfel de gauri negre ar avea o temperatura mult mai mare si ar emite radiatie cu o rata mult mai mare. O gaura neagra primordiala cu o masa initiala de un miliard de tone ar avea un timp de viata aproximativ egal cu varsta universului. Gaurile negre primordiale cu masele initiale mai mici decat aceasta valoare ar fi deja complet evaporate, dar acelea cu mase putin mai mari ar emite inca radiatii sub forma de raze X si raze gamma. Aceste raza X si gamma sunt ca undele de lumina, dar cu lungimea de unda mult mai mica. Astfel de gauri merita cu greu calificativul de negre: in realitate ele sunt alb incandescent si emit energie cu o raza de circa zece mii de megawati.
Daca s-ar putea valorifica puterea sa, o gaura neagra de acest fel ar putea actiona zece centrale electrice mari. Totusi, acest lucru ar fi dificil: gaura neagra ar avea masa unui munte comprimata in mai putin de a milioana milionime dintr-un centimetru, dimensiunea nucleului unui atom! Daca am avea o gaura neagra de acest fel la suprafata pamantului, nu ar exista nici un mijloc care s-o opreasca sa cada prin podea spre centrul pamantului. Ea ar oscila prin pamant inainte si inapoi, pana ce, in cele din urma, s-ar stabiliza in centru. Astfel ca singurul loc unde se poate pune o astfel de gaura neagra in care sa se poata utiliza energia pe care o emite ar fi pe o orbita in jurul pamantului si singurul mod in care poate fi pusa pe orbita in jurul pamantului ar fi prin remorcarea unei mase mari in fata sa, ca un morcov in fata unui magar. Aceasta nu suna ca o propunere foarte practica, cel putin nu in viitorul apropiat.
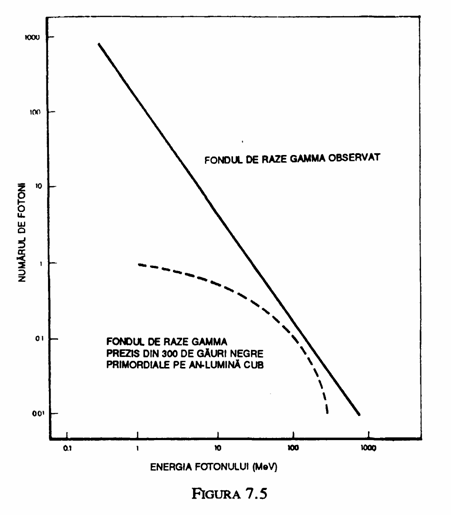
Dar, chiar daca nu putem valorifica emisia acestor gauri negre primordiale, care sunt sansele noastre de a le observa? Putem cauta razele gamma pe care le emit gaurile negre primordiale in majoritatea vietii lor. Desi radiatia celor mai multe ar fi foarte slaba deoarece ele sunt foarte indepartate, totalul radiatiilor lor ar putea fi detectabil. Intr-adevar, observam un astfel de fond de raze gamma: figura 7.5 arata modul in care intensitatea observata difera la diferite frecvente (numarul de unde pe secunda). Totusi, acest fond ar fi putut sa fie generat, si probabil a fost, de alte procese decat gaurile negre primordiale. Linia intrerupta din figura 7.5 arata modul in care ar varia intensitatea cu frecventa pentru razele gamma emise de gaurile negre primordiale, daca ar fi in medie 300 pe an-lumina cub. Aceasta limita inseamna ca gaurile negre primordiale ar fi putut forma cel mult o milionime din materia din univers.
Gaurile negre primordiale fiind atat de putine, ar parea putin probabil sa existe una destul de aproape de noi pentru a o observa ca sursa individuala de raze gamma. Dar, deoarece gravitatia ar atrage gaurile negre primordiale spre orice materie, ele trebuie sa fie mult mai multe in si in jurul galaxiilor. Astfel, desi fondul de raze gamma ne spune ca nu pot exista in medie mai mult de 300 de gauri negre primordiale pe an-lumina cub, nu ne spune nimic despre cat de multe pot fi in galaxia noastra. Daca ar fi, sa spunem, de un milion de ori mai multe decat cifra de mai sus, atunci gaura neagra cea mai apropiata de noi ar fi probabil la o distanta de circa un miliard de kilometri, sau cam tot atat de departe ca si Pluto, cea mai indepartata planeta cunoscuta. si la aceasta distanta ar fi foarte dificil sa se detecteze emisia constanta a unei gauri negre, chiar daca ar fi de zece mii de megawati. Pentru a observa o gaura neagra primordiala ar trebui sa se detecteze cateva cuante de raze gamma care vin din aceeasi directie, intr-un interval de timp rezonabil, de exemplu, o saptamana. Altfel, ele pot reprezenta pur si simplu o parte din fond. Dar principiul cuantic al lui Planck ne spune ca fiecare cuanta de raze gamma are o energie foarte inalta, astfel ca pentru a radia chiar zece mii de megawati nu sunt necesare multe cuante. Si pentru a observa aceste cateva cuante ce vin de la o distanta ca aceea la care se gaseste Pluto, ar fi necesar un detector de raze gamma mai mare decat oricare detector construit pana acum. In plus, detectorul ar trebui sa fie in spatiu, deoarece razele gamma nu pot strabate atmosfera.
Desigur, daca o gaura neagra aflata la distanta la care se gaseste Pluto ar ajunge la sfarsitul vietii sale si ar exploda, emisia exploziei finale ar fi usor de detectat. Dar, daca gaura neagra emite de zece sau douazeci de miliarde de ani, sansa de a ajunge la un sfarsit in urmatorii cativa ani, in loc de cateva milioane de ani in trecut sau in viitor, este intr-adevar foarte mica! Astfel, pentru a avea o sansa rezonabila de a vedea o explozie inainte ca fondurile pentru cercetare sa se termine, ar trebui sa se gaseasca o cale de detectare a exploziei aflate in interiorul unei distante de un an lumina si inca ar exista problema unui mare detector de raze gamma pentru a observa cele cateva cuante de raze gamma provenite din explozie. In acest caz insa, nu ar fi necesar sa se determine ca toate cuantele vin din aceeasi directie: ar fi destul sa se observe ca ele au sosit toate intr-un interval de timp, pentru a avea destula incredere ca ele provin din aceeasi explozie.
Un detector de raze gamma capabil sa depisteze gaurile negre primordiale este intreaga atmosfera a pamantului. In orice caz, noi nu putem construi un detector mai mare!) Atunci cand o cuanta de raze gamma cu energie inalta loveste atomii atmosferei noastre, ea creeaza perechi de electroni si pozitroni (antielectroni). Cand acestia lovesc alti atomi ei creeaza la randul lor mai multe perechi de electroni si pozitroni, astfel ca se obtine asa-numita cascada de electroni. Rezultatul este o forma de lumina numita radiatia Cerenkov. Prin urmare, se pot detecta impulsurile de raze gamma cautand scanteieri de lumina pe cerul noptii. Desigur, exista si alte fenomene care pot produce scanteieri pe cer, cum sunt fulgerele si reflexiile luminii solare pe sateliti si resturi de sateliti in miscare pe orbita. Impulsurile de raze gamma se pot deosebi de aceste efecte observand scanteierile simultan din doua locuri indepartate unul de celalalt. O astfel de cercetare a fost efectuata in Arizona de doi oameni de stiinta din Dublin, Neil Porter si Trevor Weekes, folosind telescoape. Ei au gasit mai multe scanteieri, dar nici una care sa poata fi atribuita sigur impulsurilor de raze gamma provenite de la gaurile negre primordiale.
Chiar daca rezultatele cautarii gaurilor negre primordiale sunt negative, ele ne dau, totusi, informatii importante despre etapele foarte timpurii ale universului. Daca universul timpuriu era haotic sau neregulat sau daca presiunea materiei era scazuta, ar fi fost de asteptat sa se produca mai multe gauri negre primordiale decat limita stabilita deja de observatiile noastre asupra fondului de raze gamma. Numai daca universul timpuriu era foarte omogen si izotrop, cu o presiune inalta se poate explica absenta unui numar mai mare de gauri negre primordiale observate.
*
Ideea radiatiilor ce provin de la gaurile negre a fost primul exemplu de prezicere care depinde in mod esential de ambele mari teorii ale acestui secol, relativitatea generalizata si mecanica cuantica. Initial, ea a starnit multe opozitii deoarece deranja punctul de vedere existent: "Cum poate o gaura neagra sa emita ceva?" Atunci cand am anuntat prima oara rezultatele calculelor mele la o conferinta la Laboratorul Rutherford-Appleton de langa Oxford, am fost intampinat cu neincredere. La sfarsitul comunicarii mele presedintele sedintei, John G. Taylor de la Kings College, Londra, a pretins ca totul era o prostie. El a scris chiar o lucrare pe aceasta tema. Totusi, in cele din urma majoritatea oamenilor, inclusiv John Taylor au ajuns la concluzia ca gaurile negre trebuie sa radieze ca si corpurile fierbinti daca ideile noastre privind relativitatea generalizata si mecanica cuantica sunt corecte. Astfel, chiar daca nu am reusit sa gasim o gaura neagra primordiala, exista un acord destul de general ca daca am fi reusit, ea ar fi trebuit sa emita o multime de raze gamma si raze X.
Existenta radiatiei gaurilor negre pare sa insemne ca colapsul gravitational nu este atat de final si ireversibil cum am crezut odata. Daca un astronaut cade intr-o gaura neagra, masa acesteia va creste, dar in cele din urma energia echivalenta masei suplimentare va fi returnata universului sub forma de radiatii. Astfel, intr-un sens, astronautul va fi "reciclat". Ar fi totusi un mod nesatisfacator de imortalitate, deoarece orice notiune personala despre timp va ajunge la sfarsit atunci cand astronautul este distrus in interiorul gaurii negre! Chiar si tipurile de particule care ar fi emise in cele din urma de gaura neagra ar fi in general diferite de acelea care formau astronautul: singura caracteristica a astronautului care ar supravietui ar fi masa sau energia sa.
Aproximatiile pe care le-am folosit pentru obtinerea emisiei gaurilor negre ar trebui sa actioneze bine atunci cand gaura neagra are o masa mai mare decat o fractiune dintr-un gram. Totusi, ele vor da gres la sfarsitul vietii gaurii negre cand masa sa devine foarte mica. Rezultatul cel mai probabil pare a fi ca gaura neagra pur si simplu va disparea, cel putin din regiunea noastra a universului, luand cu ea astronautul si orice singularitate care ar putea fi in ea, daca intr-adevar exista una. Aceasta a fost prima indicatie ca mecanica cuantica poate elimina singularitatile prezise de relativitatea generalizata. Totusi, metodele pe care eu si altii le-am utilizat in 1974 nu au putut sa raspunda intrebarilor cum este aceea daca singularitatile s-ar produce in gravitatia cuantica. Prin urmare; din 1975 am inceput sa elaborez o abordare mai puternica a gravitatiei cuantice bazata pe ideea lui Richard Feynman a sumei istoriilor. Raspunsurile pe care aceasta abordare le sugereaza pentru originea si soarta universului si elementelor sale, cum sunt astronautii, vor fi prezentate in urmatoarele doua capitole. Vom vedea ca, desi principiul de incertitudine introduce limitari asupra preciziei tuturor prezicerilor noastre, el poate elimina, in acelasi timp, lipsa fundamentala de predictibilitate care se produce la o singularitate a spatiu-timpului.