
|
|
|
Calculul densitatii energiei radiante incidente pe un plan orientat arbitrar
In vederea cercetarii posibilitatilor de valorificare a energiei radiante solare este utila cunoasterea valorilor radiatiei globale primite de unitatea de suprafata in decurs de o zi, o luna sau un anotimp in diverse zone geografice.
S-a constatat ca valorile cele mai mari ale densitatii zilnice a radiatiei solare se obtin in lunile de vara iar cele mai mici iarna, datorita influentei determinante a inaltimi Soarelui asupra acestor valori. Pentru cerul senin, densitatea zilnica din lunile de vara este in jur de 700 cal/cm2·zi, la toate statiile din tara, iar valorile medii pentru toate zilele, indiferent de starea cerului, depasesc 500 cal/cm2·zi.
Pentru a avea o imagine de ansamblu a influentei factorului metrologic, cum si a latitudinii, altitudini, reliefului asupra valorii densitatii de putere radianta solara se intocmesc harti anotimpuale si anuale pe care se traseaza curbe de aceeasi densitate a radiatiei solare.
Durata efectiva de stralucire a Soarelui reprezinta numarul de ore in care Soarele a stralucit pe cer, exprimata in ore sau zecimi de ora. Aceasta durata se obtine prin inregistrarea unor perforatii obtinute prin arderea unei diagrame de hartie innegrita, divizata in ore si jumatati de ora, ardere sub forma unui fascicul foarte ingust.
Durata relativa reprezinta raportul dintre durata efectiva si durata posibila, stabilita prin durata "zilei luminoase", determinata de pozitia Pamantului fata de Soare, ca urmare a miscarilor sale de rotatie si revolutie.
Este evident ca cu cat durata efectiva zilnica, lunara sau anuala de stralucire a Soarelui este mai mare, cu atat cantitatea de energie radianta primita de Pamant este mai mare.
Distributia valorilor duratei efective de insolatie pune in evidenta zonele cele mai insorite din timpul anului: Delta Dunarii, Litoralul Marii Negre, Campia Romana. Regiunile de ses se deosebesc intre ele ca urmare a influentei circulatiei curentilor de aer, determinata si de relieful muntos invecinat.
Valorile mai scazute ale duratei de insolatie in zonele montane si submontane se datoresc nebulozitatii crescute, caracterizata printr-o frecventa mare a numarului de zile cu ceata si cer noros sau acoperit.
Prin zi cu cer senin se denumeste acea zi in care Soarele este complet degajat de nori de la rasarit pana la asfintit. Nebulozitatea este singurul factor care stabileste numarul de zile senine intr-o perioada.
In general, numarul mediu al zilelor cu cer senin nu depaseste 50% din totalul zilelor lunii, cu exceptia statiilor din Delta Dunarii si de pe litoral care ajung uneori la peste 75% in luna august.
Gradul de opacitate al atmosferei influenteaza foarte mult valoarea densitatii puterii radiante solare. O absorbtie importanta a radiatiilor solare este exercitata in zona ecuatoriala de vaporii de apa, iar deasupra pustiurilor si a stepelor continentale - de pulberile solide din aer.
Cele mai transparente mase de aer pentru radiatiile solare sunt cele continentale antarctice, in regim anticiclonic. Dar in aceste zone Soarele are pozitii joase deasupra orizontului si ca urmare valoarea densitatii puteri radiante globale este mica.
Pentru zonele sudice ale Romaniei, valorile medii ale densitatii puterii radiante solare au atins 1,28 cal/cm2min, in cazul predominarii maselor de aer cu transparenta mare.
Umezeala ridicata a aerului in timpul lunilor de vara si poluarea atmosferei determina o scadere sensibila a valorilor densitatilor puterii de radiatie solara.
In cursul anului, intensitatea radiatiei solare directe sufera oscilatii in functie de inaltimea soarelui deasupra orizontului si de caracteristicile maselor de aer, care acopera regiunea considerata.
Factorul geometric privind radiatia solara in tara noastra. Sisteme de coordonate ceresti, [5]
Unul dintre dezavantajele energiei solare consta in faptul ca Soarele executa o miscare diurna aparenta pe bolta cereasca, din care motiv unele captatoare necesita o urmarire continua a acestei miscari. In plus aceasta miscare nu este aceeasi in fiecare zi, datorita miscarii de revolutie a Pamantului in jurul Soarelui.
Din acest motiv, chiar si in cazul folosirii unor captatoare plane care de obicei au o pozitie fixa, este necesara cunoasterea acestei miscari pentru a stabili pozitia optima de inclinare a captatorului fata de orizontala locului. Datorita miscarii diurne aparente a Soarelui pe bolta cereasca, razele solare cad asupra Pamantului sub un anumit unghi care difera de la un loc la altul, de la o ora la alta, de la o zi la alta, de la un anotimp la altul. Precizarea pozitiei relative a Soarelui fata de anumite sisteme de coordonate atasate Pamantului este absolut necesara in proiectarea si studierea instalatiilor energetice solare.
1. Puncte, directii si plane perpendiculare in rotatia diurna aparenta a sferei ceresti
Privind cerul, avem impresia ca vedem o imensa bolta, avand forma unei calote sferice, care se sprijina pe suprafata solului de-a lungul unui cerc orizontal, incat oricat s-ar deplasa observatorul, el are impresia ca se gaseste pe axa verticala a calotei.
Punctul in care verticala locului prelungita in sus inteapa sfera cereasca se numeste zenitul locului, iar punctul obtinut prelungit verticala locului in jos, se numeste nadirul locului.
Planul tangent la suprafata Pamantului intr-un loc se numeste orizontul locului. Acest plan taie sfera cereasca dupa un cerc mare, numit orizontul ceresc al locului.
Miscarea de rotatie aparenta a sferei ceresti se face in sens retrograd, de la est la vest, in jurul axei PP', axa lumii, care se confunda cu axa de rotatie a Pamantului.
In figura 1 ochiul observatorului O este in centrul sferei ceresti, iar PP' este axa lumii. Fie OZ verticala locului, iar planul perpendicular pe OZ si trecand prin O, orizontul locului. Planul dus prin axa lumii si verticala locului se numeste meridianul locului.
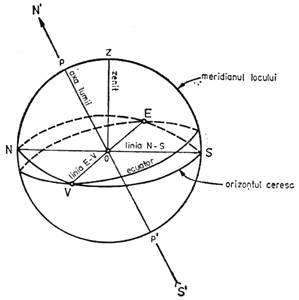
Fig. 1. Definirea unor notiuni: meridian, orizont, ecuator, zenit, axa lumii
Intersectia acestui plan cu orizontul este linia nord-sud (N-S). Planul perpendicular pe axa lumii si care trece prin O se numeste ecuator. Intersectia ecuatorului cu planul orizontului este linia est-vest.
Orice stea (de exemplu, Soarele) ia parte la miscarea aparenta diurna a boltii ceresti, parcurgand intr-o zi intregul cerc paralel.
In miscarea ei diurna, steaua σ trece la meridian in m (trecerea superioara) si in m' (trecerea inferioara) iar orizontul il taie in a (unde apune) si in r (unde rasare).
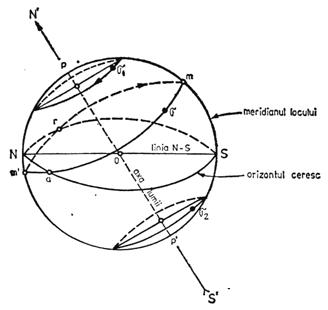
Fig. Miscarea aparenta diurna a stelei s (de exemplu Soarele)
 a.
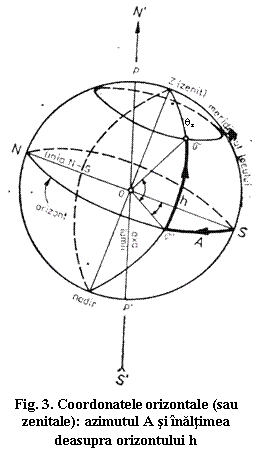
Coordonate orizontale. Fixarea
pozitiei unui astru pe bolta cereasca se face cu ajutorul a doi parametrii sau coordonate. Un
prim sistem de referinta local il constituie coordonatele orizontale
sau zenitale.
a.
Coordonate orizontale. Fixarea
pozitiei unui astru pe bolta cereasca se face cu ajutorul a doi parametrii sau coordonate. Un
prim sistem de referinta local il constituie coordonatele orizontale
sau zenitale.
![]() Elementele
fundamentale ale unui astfel de sistem sunt:
Elementele
fundamentale ale unui astfel de sistem sunt:
meridianul locului (PZP') ca cerc de origine;
orizontul locului ca plan fundamental;
OZ ca axa a sistemului.
Planul dus prin OZ si stea se numeste verticala stelei.
Unghiul masurat in jurul zenitului in sens retrograd, de la directia sud a meridianului pana la verticala stelei, se numeste azimutul A al stelei.
![]() A= S(OZ)σ
= SOσ'=arcSσ'
A= S(OZ)σ
= SOσ'=arcSσ'
El se masoara in grade de la 0o la 360o, incepand de la directia sud a meridianului in sens retrograd sau de la 0o la 180o spre apus si de la 00 la - 180o spre rasarit.
Unghiul facut de directia vizuala Oσ a astrului cu verticala OZ se noteaza cu qz si se numeste distanta zenitala a stelei.
qz ZOσ = arc Zσ
Distanta zenitala qz se masoara pe verticalul stelei σ in grade de la 0o la 90o, incepand de la zenit. In locul distantei zenitale qz se foloseste complementul ei notat cu h si numit inaltimea deasupra orizontului a stelei σ.
h = σOσ' =arc σσ'
b. Coordonate orare. Coordonatele orare alcatuiesc un alt sistem de referinta local care are elementele fundamentale:
meridianul locului (PZP') ca cerc de origine;
ecuatorul ceresc ca plan fundamental;
axa lumii (PP') ca axa a sistemului.
Planul dus prin axa lumii si steaua σ taie sfera cereasca dupa un cerc mare numit cercul orar sau de declinatie al stelei. Unghiul facut in jurul axei polilor PP' de meridianul locului cu cercul orar PσP', se numeste unghi orar al stelei σ si se noteaza cu w
w= Ec(PP')σ = CO'σ = EcOσ' = arc Ecσ'
Unghiul facut de raza vizuala a stelei σ cu planul ecuatorului se numeste declinatia stelei si se noteaza cu d
d σOσ'=arc σσ'
Declinatia se masoara pe cercul orar sau de declinatie, in grade, de la 0 la 90 incepand de la ecuator spre polul nord si de la 0 la -90 incepand de la ecuator spre polul sud.
Arcul Ps <POs=(90 d) se numeste distanta polara a stelei s. Daca steaua s este Soarele, trecerea acestuia la meridian (w=0) defineste amiaza solara locala.
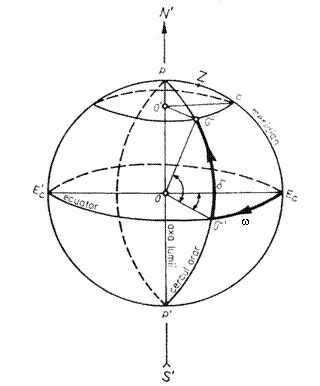
Fig. 4. Coordonatele orare: unghiul orar H si declinatia d
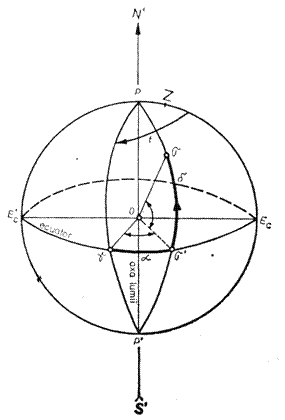
c. Coordonate ecuatoriale. Sistemul de coordonate ecuatoriale este independent de miscarea diurna, variind insa in timp.
Elementele fundamentale ale acestui sistem sunt:
cercul orar PgP' al punctului vernal g (un punct pe ecuatorul ceresc determinat de miscarea aparenta a Soarelui);
ecuatorul ceresc si axa sistemului;
axa lumii PP'.
Unghiul masurat in jurul polului in sens direct de la cercul orar PgP' al punctului vernal g pana la cercul orar PgP' al stelei s se noteaza cu a si se numeste ascensiunea dreapta a stelei s
a g( PP')s gOs'=arc gs
Ascensiunea dreapta se masoara pe ecuator in grade sau ore, ca si unghiul orar, in sens direct. A doua coordonata ecuatoriala este declinatia d, aceeasi ca in cazul coordonatelor orare:
d σ'Oσ=arc σ'σ
 Ca si la coordonatele orare,
in loc de d
se poate folosii complementul sau (90 d),
distanta polara, socotita de la 0
la 180 ,
incepand de la polul nord - P.
Ca si la coordonatele orare,
in loc de d
se poate folosii complementul sau (90 d),
distanta polara, socotita de la 0
la 180 ,
incepand de la polul nord - P.
Fig. 5. Coordonatele ecuatoriale: ascensiunea dreapta a si declinatia d
d. Coordonate eliptice
Soarele executa pe sfera cereasca, in afara de miscarea diurna aparenta si o miscare proprie printre stele, in timp de un an descriind cercul mare εε', numit ecliptica.
Normala in O la planul ecliptic se numeste axa ecliptica si intersecteaza sfera cereasca in π si π', polii eclipticii.
Unghiul w facut de planul eclipticii cu planul ecuatorului ceresc se numeste inclinarea sau oblicitatea eclipticei; el este egal cu unghiul facut de axa eclipticei cu axa lumii. Planul dus prin axa eclipticei si astrul σ taie sfera dupa un cerc mare, numit meridian ecliptic.
Planul orizontal fundamental este planul eclipticei, cel vertical este meridianul ecliptic al punctului g, iar axa este axa eclipticei.
Unghiul masurat in sens direct de la meridianul ecliptic al punctului vernal g pana la meridianul ecliptic al stelei s se noteaza cu l si se numeste longitudine cereasca:
![]()
Longitudinea cereasca se masoara pe ecliptica in sens direct de la punctul g si se exprima in grade sau ore (de la 0o la 360o sau 0 la 24h).
Unghiul b facut de raza vizuala Os cu planul eclipticei se numeste latitudine cereasca; el se masoara in grade incepand de la ecliptica, fiind pozitiv spre polul nord (00 la 90o) si negativ (0o la -90o) spre sud:
![]()
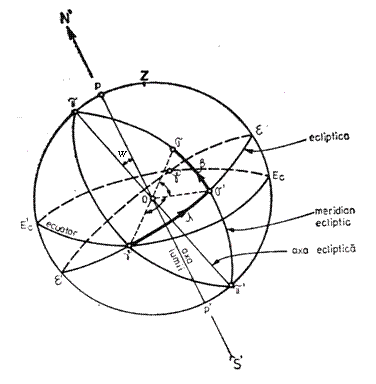
Fig. 6. Coordonatele eliptice: longitudinea cereasca l si latitudinea cereasca b
Punctele g si g' se numesc echinoctii de primavara si respectiv de toamna, iar ε si ε'- solstitii de vara si respectiv de iarna.
Latitudinea locului j, (pozitiva in emisfera nordica) este unghiul masurat de la ecuator pana la punctul de interes de pe suprafata pamantului.
Pentru proiectarea unei instalatii de conversie a energiei solare in energie termica sau electrica este necesar sa cunoastem radiatia solara disponibila pe suprafata captatoare fie a colectorului solar, fie a modulului (panoului) fotovoltaic [14].
Se considera un panou fotovoltaic directionat spre sud, (unghiul A=0). Suprafata panoului este inclinata fata de orizontala cu unghiul qincl
Radiatia solara pe suprafata colectorului va fi maximala in momentul amiezei, cand unghiul de inaltare a soarelui, h, va fi maximal, iar drumul parcurs de raza solara - minimal si unghiul orar ω = 0. Aceasta situatie va avea loc daca radiatia directa cade perpendicular pe suprafata panoului fotovoltaic. Din figura 7 rezulta ca θz = qincl
Pozitia soarelui pe bolta cereasca in punctul de interes pentru orice ora si orice zi, se determina folosind expresiile [5]:
![]() (1)
(1)
![]() (2)
(2)
Din relatia (2) cunoscand ω = 0 rezulta:
![]() (3)
(3)
deci se obtine ca unghiul de inclinare al celulelor fotovoltaice se poate determina cu relatia:
![]() (4)
(4)

Figura 7. Radiatia solara directa pe un plan inclinat
in momentul amiezei: ω=0; γ=0;
Este evident, ca perioada de interes poate fi arbitrara - o ora, o zi, o luna sau un anotimp oarecare. Astfel apare necesitatea calcului radiatiei solare pe un plan inclinat.
In general, in graficele si tabelele privind radiatia solara sunt date valorile densitatii energiei radiante incidente pe o suprafata orizontala.
Solutia optimala ar fi urmarirea soarelui in miscarea sa aparenta pe bolta cereasca astfel ca radiatia directa sa cada perpendicular pe suprafata de interes.
Sistemele solare cu panouri fotovoltaice se construiesc fara urmarire, se orienteaza spre sud si se monteaza sub un unghi fata de orizont optimal pentru localitatea data si durata de exploatare pe parcursul anului.
Densitatea de energie radianta B0 care cade pe un plan orizontal situat in afara atmosferei Pamantului este calculata cu relatia [7]:
![]() (5)
(5)
E0= 1367w/m2 - constanta solara;
n - numarul zilei din an (de exemplu n=1 la 1 Ianuarie);
j - latitudinea geografica a locului, [
d - declinatia Soarelui, [
ws - unghiul orar de rasarire al Soarelui, [
Declinatia Soarelui la amiaza solara intr-o zi oarecare n a anului se poate calcula cu formula aproximativa a lui Cooper:
![]() (6)
(6)
Unghiul orar de rasarire al Soarelui se determina cu relatia:
![]() (7)
(7)
Unghiul orar de apunere al Soarelui este:
![]() (8)
(8)
Coeficientul de transparenta kT se calculeaza pentru fiecare luna a anului cu relatia:
![]() (9)
(9)
G - densitatea de energie radianta globala pe un plan orizontal, [Wh/m2·zi].
Coeficientul de transparenta determina atenuarea medie a radiatiei solare de catre atmosfera, pentru o locatie si o luna precizate.
Densitatea de energie difuza D pe un plan orizontal se poate determina cu relatia:
![]() (10)
(10)
Densitatea de energie directa B pe un plan orizontal este:
![]() (11)
(11)
Densitatea de energie directa B(qincl) ce cade pe un panou fotovoltaic inclinat cu un unghi qincl fata de orizontala este:
![]() (12)
(12)
unde:
![]() (13)
(13)
ws - in acest caz este unghiul orar de rasarire a Soarelui de deasupra orizontului dat, calculat cu relatia 5.
![]() (14)
(14)
![]() - este unghiul orar de
rasarire a Soarelui de deasupra unui plan inclinat cu unghiul qincl
fata de orizontala.
- este unghiul orar de
rasarire a Soarelui de deasupra unui plan inclinat cu unghiul qincl
fata de orizontala.
Presupunand ca radiatia difuza este distribuita izotrop pe bolta cereasca, atunci densitatea de energie difuza ce cade pe un plan inclinat este:
![]() (15)
(15)
Densitatea de energie reflectata de sol (Pamant) este in general foarte mica si este determinata de relatia:
![]() (16)
(16)
r - coeficient de reflexie a suprafetei pamantului.
Tabelul 1. Valorile tipice ale coeficientul de reflexie
Caracteristicile terenului
Coeficientul de reflexie, r
Aratura
0,2
Teren acoperit cu verdeata
0,3
Desert nisipos
0,4
Teren acoperit cu zapada
0,5 0,8
Astfel, se poate determina radiatia globala G(qincl) pe o suprafata inclinata ca suma a radiatiilor directa, difuza si reflectata:
![]() (17)
(17)
Exemplu de calcul
Pentru orasul Craiova coordonatele geografice sunt:
A latitudine j 44,23
A longitudine l 23,87
Calcularea declinatiei medii pe fiecare luna se realizeaza prin stabilirea zilei pentru care valoarea declinatiei este mai aproape de valoarea declinatiei medii a lunii considerate.
De exemplu, pentru ziua de 1 Ianuarie (n=1) declinatia este:
![]()
Tabelul Calculul declinatiei pentru zilele lunii Ianuarie
Ziua
din luna Ianuarie
Declinatia
d
Ziua
din luna Ianuarie
Declinatia
d
1
-23,0116
16
-21,0963
2
-22,9305
17
-20,917
3
-22,8427
18
-20,7314
4
-22,748
19
-20,5397
5
-22,6466
20
-20,3419
6
-22,5385
21
-20,138
7
-22,4237
22
-19,9282
8
-22,3023
23
-19,7125
9
-22,1742
24
-19,491
10
-22,0396
25
-19,2636
11
-21,8985
26
-19,0306
12
-21,7509
27
-18,7919
13
-21,5968
28
-18,5477
14
-21,4363
29
-18,2979
15
-21,2695
30
-18,0428
31
-17,7823
Media declinatiei lunare
-20,8472
Se constata ca valoarea declinatiei calculata pentru ziua 17 este ce-a mai apropiata de valoarea declinatiei medii lunare. Analog se determina zilele de calcul pentru celelalte luni.
Tabelul 3. Valorile declinatiei corespunzatoare zilei de calcul a lunilor din an
Luna
Ziua de calcul
Declinatia
d
Luna
Ziua de calcul
Declinatia
d
Ianuarie
17 (n=17)
-20,9
Iulie
17 (n=198)
21,2
Februarie
16 (n=47)
-13,0
August
16 (n=228)
13,5
Martie
16 (n=75)
-2,4
Septembrie
15 (n=258)
2,2
Aprilie
15 (n=105)
9,4
Octombrie
15 (n=288)
-9,6
Mai
15 (n=135)
18,8
Noiembrie
14 (n=318)
-18,9
Iunie
11 (n=162)
23,1
Decembrie
10 (n=344)
-23,0
Declinatia medie anuala este: d=0,033. Unghiul de inclinare optim anual este:
![]()
Calculul densitatii de energie radianta pe o suprafata inclinata pentru luna Ianuarie se realizeaza pornind de la cunoasterea valorii densitatii de energie radianta pe o suprafata orizontala (tabel 4).
Tabelul 4. Densitatea de energie radianta pe un plan orizontal
Densitatea de energie radianta
Ian.
Feb.
Mar.
Apr.
Mai
Iunie
Iulie
August
Sept.
Oct.
Noiembrie
Decembrie
G
[kWh/m2·zi]
1,44
2,25
3,42
4,58
5,58
6,19
6,53
5,59
4,06
2,69
1,72
1,22
Sursa: RetScreen Data Base [13]
Densitatea de energie radianta B0:
![]()
E0= 1367w/m2;
n=17;
j 44,23
d -20,9
![]()
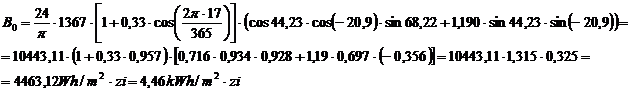
Coeficientul de transparenta:
![]()
Densitatea de energie difuza D pe un plan orizontal:
![]()
Densitatea de energie directa B pe un plan orizontal este:
![]()
Densitatea de energie directa B(qincl) ce cade pe un captator inclinat cu un unghi qincl fata de orizontala este:
![]()
![]()
![]()
![]()
![]()
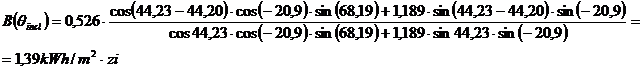
Densitatea de energie difuza ce cade pe un plan inclinat este:
![]()
Densitatea de energie reflectata de Pamant este:
![]()
Astfel, se poate determina radiatia globala G(qincl) pe o suprafata inclinata ca suma a radiatiilor directa, difuza si reflectata:
![]()
In mod analog se calculeaza densitatea de radiatie globala G(qincl) pe o suprafata inclinata pentru celelalte luni ale anului (tabel 5).
Tabelul 5. Densitatea de radiatie globala pe o suprafata inclinata
Lunile anului
B0
[kWh/m2·zi]
kt
G
kWh/m2·zi
D
kWh/m2·zi
B
kWh/m2·zi]
B(qincl
kWh/m2·zi![]()
D(qincl
kWh/m2·zi
R(qincl
kWh/m2·zi
G(qincl
kWh/m2·zi
Ian.
4,467
0,22
1,44
0,915
0,524
1,398
0,785
0,061
2,245
Feb.
6,029
0,37
2,25
1,301
0,948
1,916
1,116
0,096
3,129
Mar.
7,638
0,447
3,42
1,689
1,730
2,577
1,450
0,145
4,172
Apr.
8,643
0,530
4,58
1,832
2,741
3,027
1,573
0,194
4,794
Mai
8,643
0,645
5,58
1,509
4,070
3,606
1,295
0,237
5,139
Iunie
8,265
0,748
6,19
0,951
5,238
4,205
0,816
0,263
5,284
Iulie
7,918
0,824
6,53
0,444
6,085
5,103
0,381
0,277
5,762
August
7,767
0,719
5,59
1,043
4,54
4,555
0,896
0,237
5,688
Sept.
7,225
0,561
4,06
1,481
2,578
3,394
1,272
0,172
4,838
Oct.
6,017
0,447
2,69
1,331
1,358
2,477
1,142
1,114
3,734
Noi.
4,626
0,371
1,72
0,997
0,722
1,785
0,856
0,073
2,715
Dec.
3,933
0,310
1,22
0,792
0,427
1,244
0,680
0,052
1,976
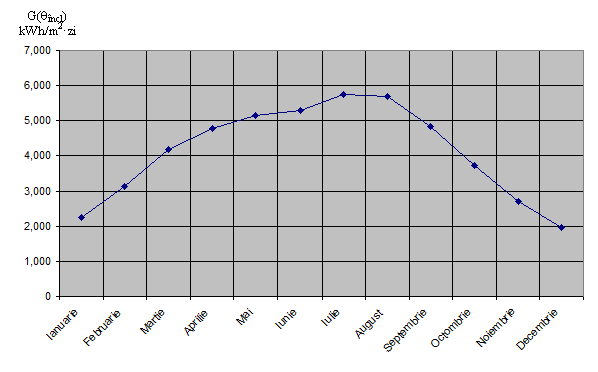
Fig. 8. Densitatea de energie radianta anuala pentru orasul Craiova
pe un plan inclinat orientat cu unghiul optim anual de 44,20
Potentialul solar din Romania [11] este reprezentat de densitatea medie de energie aferenta radiatiei solare incidente, in plan orizontal, care depaseste 1000 kWh/m2 - an.
In Romania s-au identificat cinci zone geografice, diferentiate in functie de nivelul fluxului energetic inregistrat.
Tabelul 6. Distributia potentialului energetic solar din Romania
Zona
Potential energetic solar
I
peste 1250kWh/m2 - an
II
1250 kWh /m2 - an 1150 kWh /m2 - an
III
1150 kWh /m2 - an 1050 kWh /m2 - an
IV
1050 kWh /m2 - an 950 kWh /m2 - an
V
sub 950 kWh /m2 - an
Potentialul exploatat pentru utilizarea energiei solare ca sursa de energie electrica, este ridicat, iar conversia energiei solare in energie electrica se realizeaza cu instalatii fotovoltaice care cuprind module solare, in configuratii si de dimensiuni diferite.
Costul investitiei pentru realizarea sistemelor fotovoltaice a avut o evolutie favorabila; in ultimele decenii, costul unui modul solar s-a diminuat treptat, ajungandu-se in prezent la un nivel de aproape 6$/Winstalat.
Desi pretul energiei electrice din surse solare fotovoltaice variaza in functie de conditiile obiective de instalare si exploatare, pentru alimentarea cu energie a unor consumatori izolati si de putere mica, aceste sisteme ofera o alternativa economica atractiva, daca se au in vedere, in principal, costurile ridicate necesare pentru racordarea la retea a acestor consumatori. Procesul de valorificare superioara a surselor regenerabile de energie din Romania contribuie la siguranta aprovizionarii cu energie, reducerea dependentei de importul de resurse energetice primare si dezvoltarea durabila pe termen lung, cu indeplinirea conditiilor de protectia mediului si incadrarea in reglementarile in domeniu ale Uniunii Europene.