Legea circuitului magnetic

Legea circuitului magnetic

Se considera campul magnetic produs de o spira circulara parcursa de curentul i (fig. 3.20), situata in vid (aer).

Calculand integrala de linie a vectorului inductie magnetica de-a lungul unui contur inchis (G) care inlantuie spira, se obtine:

(3.47)

Cand curba G nu inconjoara linii de curent, integrala de linie a inductiei electrice este nula:

, (3.48)

iar cand curba G inconjoara mai multe conductoare parcurse de curent, aplicand principiul suprapunerii, se deduce:

. (3.49)

Daca conturul G inlantuie o bobina cu n spire parcurse de curentul i, relatia (3.49) devine:

. (3.50)

In general cand conturul strabate mai multe bobine, relatia (3.50) devine:

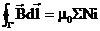. (3.51)

Inlocuind in ultima relatie pe si , se obtine formularea obisnuita a legii circuitului magnetic in regim stationar.

. (3.52)

Integrala de linie a vectorului intensitatii campului de-a lungul unui contur inchis G se numeste tensiune magnetomotoare (t.m.m.), iar suma algebrica a curentilor de conductie care strabat suprafata limitata de conturul G se numeste solenatie (Q). Se foloseste termenul solenatie in loc de intensitatea curentului electric de conductie, deoarece ultima marime caracterizeaza un conductor, iar solenatia se refera la o suprafata strabatuta de mai multe conductoare sau de acelasi conductor de mai multe ori (de N ori).

In regim stationar, legea circuitului magnetic se enunta astfel: tensiunea magnetomotoare de-a lungul oricarei curbe inchise este egala cu suma algebrica a curentilor de conductie care strabat suprafata deschisa limitata de curba respectiva. Semnul curentilor in scrierea sumei algebrice se asociaza sensului de integrare pe curba inchisa dupa regula burghiului drept (fig. 3.20), adica:

.

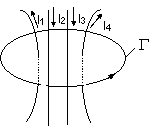
Fig. 3.19Fig. 3.20

In regim variabil, legea circuitului magnetic are urmatorul enunt: tensiunea magnetomotoare de-a lungul oricarei curbe inchise este egala cu curentul total care strabate suprafata deschisa limitata de curba respectiva. Prin curent total se intelege suma dintre: solenatie, curentul de deplasare si curentul de conventie; deci:

. (3.53)

In cazul corpurilor imobile, curentul de convectie este nul si legea circuitului magnetic devine:

. (3.54)

Din relatia (3.54) rezulta ca orice variatie in timp a campului electric (prin curentul de deplasare) da nastere unui camp magnetic, care impreuna cu campul electric reprezinta campul electromagnetic unic. Aceasta relatie reprezinta prima din ecuatiile lui Maxwell (ecuatiile campului electromagnetic), care stabileste legatura dintre campul electric si campul magnetic.

Se numeste regim cvasistationar regimul variabil in care poate fi neglijat curentul de deplasare cu exceptia dielectricului condensatoarelor; in acest regim legea circuitului magnetic are aceeasi forma ca in regimul stationar.

. (3.55)

Ca regim cvasistationar poate fi considerat regimul de functionare a retelelor de curent alternativ la frecventa industriala.

Legea circuitului magnetic este folosita la calculul campului magnetic in anumite situatii cand aplicarea formulei Biot-Savart-Laplace este dificila, precum si in calculul circuitelor magnetice.

In sistemul MKSA rationalizat, solenatia se masoara in amperspire, iar tensiunea magnetomotoare se masoara in amperi sau amper-spire (A.sp.).

1.   A.sp = 4p unitati MKSA nerationalizate = 4p m Oem =4p decigilbert (dGb)=gilbert (Gb); forma rationalizata a sistemelor CGSem si CGSes nu se utilizeaza in tehnica.

Aplicatie

a)   Se considera un tor (inel) bobinat uniform cu o infasurare de N spire parcurse de curentul continuu i si se cere determinarea intensitatii campului magnetic in punctele P₁, P, P₂, folosind legea circuitului magnetic (fig. 3.21).

Se calculeaza integrala de linie a vectorului intensitatii de-a lungul a trei curbe care trec prin punctele respective. Integrala de linie a vectorului de-a lungul conturului este nula deoarece suprafata nu este strabatuta de curenti; de asemenea, integrala de linie a vectorului de-a lungul conturului este strabatuta de o solenatie totala nula. Deci campul magnetic in afara bobinajului este nul. Aplicand legea circuitului magnetic de-a lungul conturului G, care coincide cu o linie de camp si tinand seama ca , iar este constant de-a lungul conturului (din motive de simetrie), rezulta:

, (3.56)

unde l este lungimea medie a torului .

Cand raza torului tinde spre infinit, torul se transforma intr-un solenoid infinit lung, iar campul in interiorul solenoidului respectiv se calculeaza tot cu relatia (3.56).

b)  Calculul campului magnetic al unei particule electrizate in miscare lenta. In jurul particulei electrizate in miscare se produce un camp magnetic ale carui linii trebuie sa fie, din motive de simetrie, niste cercuri G cuprinse intr-un plan perpendicular pe directia de deplasare a particulei, avand centrul pe dreapta suport a vitezei (fig. 3.22).

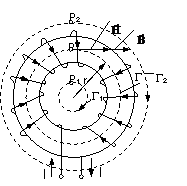
Fig. 3.21 Fig. 3.22

Calculand integrala de linie a vectorului , de-a lungul unei linii de camp de raza r, rezulta:

. (3.57)

Conform legii circuitului magnetic, trebuie sa fie egala cu curentul de deplasare care trece prin suprafata , deoarece nu exista curent de conductie (relatia 3.54 in care ):

. (3.58)

Pentru simplificare se alege suprafata o calota sferica de raza R, iar deplasarea particulei se considera suficient de lenta pentru a se pastra caracterul coulombian al campului electric.

Calculul curentului de deplasare:

. (3.59)

Aria calotei sferice este:

(3.60)

Inlocuind in relatia (3.59) se obtine:

Curentul de deplasare devine:

si tinand seama ca:

,

de unde:

rezulta:

. (3.61)

Din relatiile (3.57), (3.58) si (3.61) obtinem:

, (3.62)

iar vectorial se poate scrie:

. (3.63)

Se observa ca relatia (3.63) prezinta o mare analogie cu formula lui Biot-Savart-Laplace (relatia 3.31) daca se inlocuieste cu .