
|
|
|
DINAMICA FLUIDELOR
1 CURGEREA FLUIDELOR. ECUATIA DE CONTINUITATE.
Pentru descrierea miscarii
unui fluid se adopta metoda dezvoltata de L. Euler, conform
careia se cunosc in fiecare moment si in fiecare punct al fluidului
valorile urmatorilor parametri: viteza ![]() , densitatea r, presiunea p.
, densitatea r, presiunea p.
Curgerea unui fluid poate fi considerata:
- stationara, daca viteza ![]() a fluidului in fiecare
punct este constanta. Prin
urmare, intr-un punct dat al fluidului, viteza oricarui element de fluid
ce trece prin el este totdeauna aceeasi.
a fluidului in fiecare
punct este constanta. Prin
urmare, intr-un punct dat al fluidului, viteza oricarui element de fluid
ce trece prin el este totdeauna aceeasi.
- nestationara, daca viteza fluidului intr-un punct dat depinde de timp.
Curgerea unui lichid printr-o conducta prezinta doua tipuri limita de regimuri de curgere:
- curgerea laminara in care elementele de volum de fluid se misca regulat si paralel.
- turbulenta, caracterizata printr-o variatie a vitezelor in mod neregulat de la punct la punct si de la un moment la altul. Turbioanele sunt dispuse dezordonat fata de directia generala de curgere si liniile de curent sunt asezate neregulat unele fata de celelalte.
Curgerea unui fluid poate fi compresibila sau incompresibila dupa cum fluidul considerat este compresibil sau nu.
Analog, curgerea poate fi vascoasa sau nevascoasa dupa cum fluidul este vascos sau ideal.
Se defineste linia de curent ca fiind traiectoria descrisa de un element de fluid in miscarea sa (Fig.1.6.).
O linie de curent se caracterizeaza prin aceea ca vectorul viteza al elementului de fluid este tangent la linie in fiecare punct al sau.
In cazul unei curgeri stationare liniile de curent nu se pot intersecta intre ele.
Totalitatea liniilor de curent care trec printr-un contur inchis formeaza un tub de curent (Fig.1.6.). Intr-o curgere stationara liniile de curent din
interiorul unui tub de curent nu pot parasi tubul.
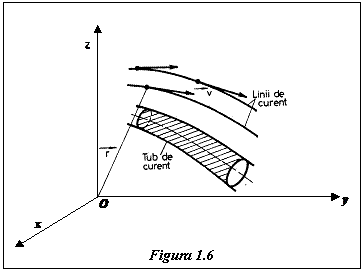
Fluidul care intra la un
capat al tubului trebuie sa iasa prin celalalt capat.
O marime caracteristica unui fluid aflat in miscare o constituie debitul volumic Qv, al acestuia.
Prin definitie, debitul volumic printr-o suprafata data reprezinta mari-mea fizica numeric egala cu un volum de fluid ce trece in unitatea de timp prin acea suprafata.
![]() (1.34)
(1.34)
Unitatea de masura in S. I. este m3/s.
Daca debitul volumic variaza de la un moment la altul prin suprafata considerata, relatia (1.34.) defineste valoarea medie a debitului in timpul t. Pentru a defini valoarea momentana a debitului volumic, se considera un interval de timp infinitezimal dt si se noteaza cu dV volumul de fluid ce trece in acest interval prin suprafata considerata. Debitul volumic se poate defini atunci prin relatia:
![]() (1.35)
(1.35)
Se defineste debitul masic Qm, al fluidului printr-o suprafata data, ca fiind marimea fizica egala cu masa de fluid ce trece in unitatea de timp prin suprafata respectiva.
![]() (1.36)
(1.36)
Unitatea de masura in S. I. este kg/s.
![]() (1.37)
(1.37)
rezulta urmatoarea relatie de legatura intre cele doua marimi Qv si Qm.
![]() (1.38)
(1.38)
Ecuatia de continuitate care constituie una dintre ecuatiile fundamentale din dinamica fluidelor exprima de fapt legea conservarii masei de fluid.
se numeste vectorul densitatii fluxului de masa. Directia sa coincide cu cea a miscarii fluidului, iar marimea sa determina cantitatea de fluid care trece in unitatea de timp prin unitatea de suprafata dispusa normal la directia de miscare.
![]()
2 ECUATIA DE MISCARE A LUI EULER
Problema fundamentala urmarita in curgerea fluidelor adica in dinamica fluidelor o constituie determinarea campului de presiune si a campului de viteze ale unui fluid aflat in miscare.
Aceste marimi sunt determinate de ecuatia lui Euler, care este ecuatia de miscare a unui fluid.
Pentru a deduce aceasta ecuatie se va considera un element de volum infinitezimal din fluidul aflat in miscare, de masa dm si avand forma unui paralelipiped cu laturile dx, dy, dz. Asupra fluidului pot actiona forte de suprafata si forte volumice.
Forta de suprafata rezultanta, care actioneaza asupra intregului element de volum considerat, va fi deci:
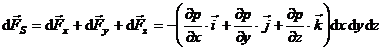
sau
![]()
![]() (1.40)
(1.40)
unde p este gradientul campului de presiune p(x,y,z), adica:
![]() (1.41)
(1.41)
Asupra acestui element de fluid se exercita
si o forta volumica a carei valoare raportata la
unitatea de masa se noteaza cu ![]() . Forta de volum ce actioneaza asupra
elementului de fluid dV se va exprima prin relatia:
. Forta de volum ce actioneaza asupra
elementului de fluid dV se va exprima prin relatia:
![]() (1.42)
(1.42)
Forta rezultanta ce actioneaza asupra elementului de fluid considerat are expresia:
![]()
![]() (1.43)
(1.43)
Aceasta forta determina o miscare accelerata a fluidului in conformitate cu legea a doua a lui Newton:
![]() (1.44)
(1.44)
unde ![]() si
si ![]()
Din expresiile (1.43.) si (1.44.) se obtine:
![]()
![]() (1.45)
(1.45)
Deoarece elementul de volum dV = dxdydz este arbitrar ales:
![]()
![]() (1.46)
(1.46)
Expresia (1.46) reprezinta ecuatia de miscare a lui Euler pentru un fluid ideal, scrisa sub forma vectoriala.
Aceasta ecuatie, impreuna cu
ecuatia de continuitate si conditiile initiale si de
marginire corespunzatoare, determina complet campul de viteze ![]() si campul de
presiune
si campul de
presiune ![]() , daca se presupune ca fluidul este incompresibil (r =const.)
si se cunoaste forta de volum raportata la unitatea de
masa,
, daca se presupune ca fluidul este incompresibil (r =const.)
si se cunoaste forta de volum raportata la unitatea de
masa, ![]() .
.
In cazul unui fluid compresibil este utila o relatie termodinamica pentru densitate, de exemplu de forma r r(p) ca in cazul fluidelor barotrope.
In cazul unui fluid in repaus ![]() , deci in absenta oricarei forte externe,
rezulta:
, deci in absenta oricarei forte externe,
rezulta:
p=0 (1.47)
deci p = const. pentru orice punct din masa fluidului.
Daca asupra fluidului in repaus
singura forta exterioara de volum care actioneaza este
aceea determinata de campul gravitational ![]() , expresia (1.46.) devine:
, expresia (1.46.) devine:
![]()
![]() deci
deci ![]() (1.48)
(1.48)
adica regasim legea fundamentala a staticii fluidelor.
In cazul unei curgeri stationare, deci cand
intr-un punct din masa fluidu-lui viteza nu depinde de timp , ![]() si ecuatia
lui Euler (1.73.) devine:
si ecuatia
lui Euler (1.73.) devine:
![]()
![]()
![]() (1.49)
(1.49)
3 ECUATIA LUI BERNOULLI
Sa consideram miscarea unui fluid ideal si incompresibil printr-un tub de curent (sau conducta), presupunand ca singura forta exterioara de volum ce actioneaza asupra sa este aceea datorata campului gravitational.
Asupra unui element de volum
actioneaza forta de volum de greutate ![]() , care raportata la unitatea de masa are expresia:
, care raportata la unitatea de masa are expresia:
![]() (1.50)
(1.50)
![]() are componentele gx=0 gy=0 gz=-g Prin inlocuirea expresiei (1.50.) in
ecuatia de miscare a lui Euler (1.46.), se obtine pe componente:
are componentele gx=0 gy=0 gz=-g Prin inlocuirea expresiei (1.50.) in
ecuatia de miscare a lui Euler (1.46.), se obtine pe componente:
![]() ,
, ![]() ,
, ![]() (1.51)
(1.51)
Inmultind prima din ecuatiile (1.51.) cu dx, a doua cu dy si a treia cu dz si insumandu-le membru cu membru, rezulta:
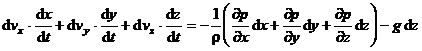 sau
sau
![]() (1.52)
(1.52)
Deoarece v2=vx2+vy2+vz2 prin diferentiere se obtine d(v2)=2(vxdvx+
vydvy+vzdvz) Ecuatia (1.52.) se mai poate scrie sub forma:
![]() (1.53)
(1.53)
Tinand seama ca fluidul este incompresibil (r=const) si g=const, ecu-atia (1.53.) se scrie:
![]() (1.54)
(1.54)
De aici, rezulta:
![]() (1.55)
(1.55)
care exprima legea lui Daniel Bernoulli pentru un fluid ideal, incompresibil care se misca in camp gravitational.
Termenul 1/2rv2 se numeste presiune dinamica a fluidului, termenul rgz este presiunea hidrostatica, iar p se numeste presiune statica. Legea lui Bernoulli se poate enunta astfel:
Intr-o curgere stationara a unui fluid ideal, incompresibil, aflat in camp gravitational, suma dintre presiunea dinamica, hidrostatica si statica ramane constanta de-a lungul unei linii de curent.