
|
|
|
Studiul rezonantei in circuitele electrice de curent alternativ
1. Notiuni fundamentale.
1.1. Marimi caracteristice curentului alternativ (ca) sinusoidal.
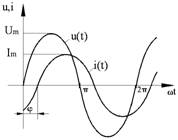
1.2.2. Variatiile in timp ale parametrilor electrici sunt descrise de rel.1, cu semnificatiile din fig.1.
![]()
![]() (1)
(1)
unde: Um,
Im reprezinta
amplitudinile tensiunii si curentului, ![]() [rad/s] (f-frecventa [Hz], T - perioada [s] ),
[rad/s] (f-frecventa [Hz], T - perioada [s] ), ![]() faza [rad].
faza [rad].
Caracterizarea si rezolvarea circuitelor electrice in regim periodic sinusoidal se poate face atat analitic (prin rezolvarea analitica a ecuatiilor circuitului) cat si prin metoda fazorilor.
Fig.1
1.1.2. Valori medii si valori patratice medii (efective, eficace) ale curentilor alternativi sinusoidali:
-Valori
medii: prin definitie, valoarea
medie este data de: 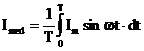 (fig.2):
pentru o perioada T, valoarea medie este zero; pentru o semiperioada, valoarea medie are expresia:
(fig.2):
pentru o perioada T, valoarea medie este zero; pentru o semiperioada, valoarea medie are expresia:
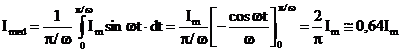
![]() (2)
(2)
-Valori medii patratice (efective):
![]()
Fig. 2 ![]() (3)
(3)
-Puterea in ca:
aparenta
: ![]() [VA]; activa:
[VA]; activa: ![]() [W];reactiva:
[W];reactiva: ![]() [VAR]; (4,5,6)
[VAR]; (4,5,6)
(![]() - factorul de putere).
- factorul de putere).
Puterilor prezentate le
corespund energiile activa ![]() [J, kWh] , disipata pe rezistoare, respectiv reactiva
[J, kWh] , disipata pe rezistoare, respectiv reactiva ![]() [VARh], acumulata in bobine si condensatoare.
[VARh], acumulata in bobine si condensatoare.
1.2. Caracteristici ale elementelor de circuit in ca sinusoidal.
 1.2.1.
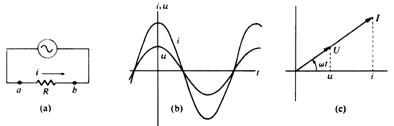
Circuitul cu rezistor ideal (fig.3), in
care:
1.2.1.
Circuitul cu rezistor ideal (fig.3), in
care: ![]()
![]() ;
; ![]()
Circuitul cu rezistor se caracterizeaza prin :
rezistenta (activa) ![]() si
si
factorul de putere ![]()
Fig.3
1.2.2. Circuitul cu bobina ideala (fig.4). Tensiunea pe bobina si curentul in circuit sunt:
![]() ;
; ![]()
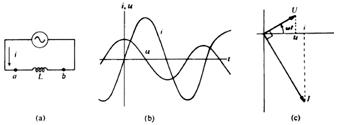 fazorial
(fig.4c):
fazorial
(fig.4c): ![]()
unde ![]() [Ω] este reactanta inductiva.
[Ω] este reactanta inductiva.
defazarea
curentului fata de tensiunea aplicata este : ![]() (curentul in urma tensiunii).
(curentul in urma tensiunii).
factorul de putere ![]()
Fig.4
1.2.3. Circuitul cu condensator (fig.5).
Tensiunea pe condensator si curentul
in circuit sunt date de: ![]() si
si 
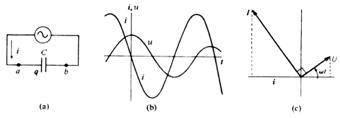
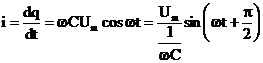 ;
;
![]() , unde:
, unde: ![]() [Ω] este
[Ω] este
reactanta capacitiva.
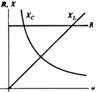 Fig.5Defazarea
curentului fata de tensiunea aplicata
Fig.5Defazarea
curentului fata de tensiunea aplicata
este ![]() (curentul in avans fata de tensiune).
(curentul in avans fata de tensiune).
factorul de putere ![]()
Variatiile parametrilor R, XL si XC functie de pulsatie
sunt prezentate in fig.6.
Fig.6
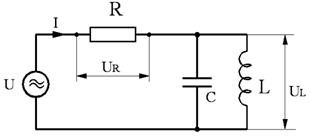
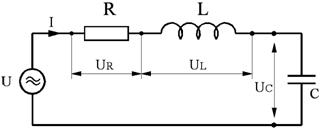
1.2.4. Circuitul RLC serie in ca. (fig.7).
Aplicand
circuitului tensiunea ![]() rezulta curentul
rezulta curentul ![]() Conform legii a II-a a lui Kirchoff :
Conform legii a II-a a lui Kirchoff : ![]() , respectiv
, respectiv ![]() (
(![]() sau, cu valori eficace :
sau, cu valori eficace :
![]() (7)
(7)
Conform reprezentarii fazoriale din fig.7, se identifica
ecuatia : ![]() cu care legea lui Ohm devine:
cu care legea lui Ohm devine: ![]() (8)
(8)
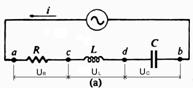 unde :
unde :![]() Ω] este impedanta circuitului.
Ω] este impedanta circuitului.
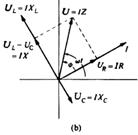
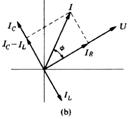
Fig.7 Fig.8
Defazajul dintre tensiune si curent este: 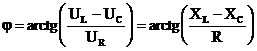
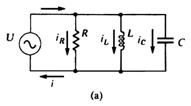
1.2.5. Circuitul RLC paralel in ca. (fig.8).
Cu
aceleasi semnificatii ca si la pct. anterior, prin aplicarea legii a I-a a lui
Kirchoff : ![]() , respectiv
, respectiv ![]() ;
; ![]()
![]() (9)
(9)
in care: ![]() - conductanta
[Ω-1] ;
- conductanta
[Ω-1] ; 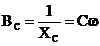 - susceptanta capacitiva [Ω-1];
- susceptanta capacitiva [Ω-1];
![]() -susceptanta inductiva [Ω-1];
-susceptanta inductiva [Ω-1]; ![]() -admitanta [Ω-1]
-admitanta [Ω-1]
Defazajul dintre
curent si tensiune: 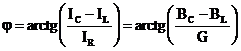 [rad]
[rad]
1.3. Rezonanta in ca.
Conditia de rezonanta este anularea defazajelor introduse de elementele reactive, care se obtine pentru:
![]() , respectiv
, respectiv ![]()
Aceasta
egalitate se obtine pentru : ![]() , respectiv
, respectiv ![]() (10, 11)
(10, 11)
unde v0 f0 sunt pulsatia si frecventa de rezonanta.
1.3.1. Rezonanta in circuitul RLC serie.
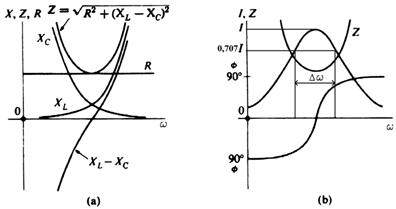
 pentru circuitul din fig.6, variatiile
impedantei Z, ale rezistentei
R si reactantelor XL si XC, precum si a unghiului de defazaj w dintre tensiunea aplicata la bornele circuitului
si curentul prin circuit sunt
prezentate in fig.9. Se observa ca la frecventa (pulsatia) de rezonanta, impedanta circuitului este
minima si egala cu R, iar curentul este maxim:
pentru circuitul din fig.6, variatiile
impedantei Z, ale rezistentei
R si reactantelor XL si XC, precum si a unghiului de defazaj w dintre tensiunea aplicata la bornele circuitului
si curentul prin circuit sunt
prezentate in fig.9. Se observa ca la frecventa (pulsatia) de rezonanta, impedanta circuitului este
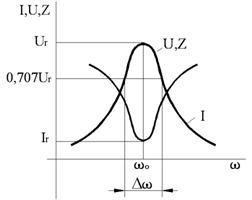
minima si egala cu R, iar curentul este maxim: ![]() . Caderile de tensiune ULr si UCr sunt egale si in opozitie de faza si ele pot fi mult mai mari decat tensiunea de
alimentare, drept care rezonanta in circuitul RLC serie se mai numeste
si rezonanta de tensiune.
. Caderile de tensiune ULr si UCr sunt egale si in opozitie de faza si ele pot fi mult mai mari decat tensiunea de
alimentare, drept care rezonanta in circuitul RLC serie se mai numeste
si rezonanta de tensiune.
Fig.9. Fig.10.
Se
defineste factorul de calitate al circuitului prin ![]() ; daca
Q>1, in circuit apar supratensiuni pe
bobine si condensatoare. Un
asemenea circuit poate fi folosit drept filtru "trece banda", prin banda Dv se intelege domeniul de variatie al pulsatiei
(frecventei) in jurul valorii de rezonanta, in care curentul
scade fata de valoarea maxima de
; daca
Q>1, in circuit apar supratensiuni pe
bobine si condensatoare. Un
asemenea circuit poate fi folosit drept filtru "trece banda", prin banda Dv se intelege domeniul de variatie al pulsatiei
(frecventei) in jurul valorii de rezonanta, in care curentul
scade fata de valoarea maxima de ![]() ori(
ori(![]()
1.3.2. Rezonanta in circuitul RLC paralel.
pentru
circuitul din fig.8, curentul in circuit, la rezonanta, este: ![]() . in aceasta situatie, susceptibilitatile
sunt egale:
. in aceasta situatie, susceptibilitatile
sunt egale: ![]() , de unde rezulta
, de unde rezulta ![]() (R reprezinta de obicei rezistenta
de pierderi echivalenta si in configuratia paralela are o
valoare mare). Curentii
(R reprezinta de obicei rezistenta
de pierderi echivalenta si in configuratia paralela are o
valoare mare). Curentii
![]() si
si ![]() sunt egali
si in opozitie de faza (
sunt egali
si in opozitie de faza (![]() ) si ei pot fi mult mai
mari decat curentul
) si ei pot fi mult mai
mari decat curentul ![]() . rezonanta
in circuitul RLC paralel se mai numeste
si rezonanta de curent.
. rezonanta
in circuitul RLC paralel se mai numeste
si rezonanta de curent.
Impedanta grupului LC paralel si corespunzator caderea de tensiune pe acesta sunt prezentate calitativ in fig.10. Acest circuit poate fi folosit drept filtru "opreste banda" (filtru "dop").
Factorul de calitate Q = ILr/I ULr/Ur.
2. Aplicatii:
1). Se considera schema din fig.7, cu valorile: U=100 Vca; R=500 Ω; L=1/p H; C=1/(4p106) F.
Se cere determinarea prin calcul :
- frecventa de rezonanta f0 [Hz];
- impedantele XLr si XCr [Ω];
- curentul prin circuit Ir;
- caderile de tensiune URr , ULr si UCr ;
- factorul de calitate al circuitului Q [-] ;
- latimea benzii de trecere Df [Hz].
 2).
Se realizeaza montajele din fig.11 si fig.12.
2).
Se realizeaza montajele din fig.11 si fig.12.
Fig.11.Fig.12
Se alimenteaza circuitele cu un semnal cu tensiune constanta si frecventa variabila, de la un generator de semnal si se masoara caderile de tensiune pe elementele de circuit.
- Valorile masurate si cele calculate se inscriu in tabelele 1 si 2, pentru cele doua circuite;
- Se vor trasa variatiile I(f) si UL(f) in jurul frecventei de rezonanta f0 .
Se vor determina latimile de banda caracteristice celor doua circuite si se vor discuta rezultatele obtinute.
|
Nr. crt. |
R Ω |
L H |
C F |
f0calc Hz |
XLr Ω |
XCr Ω |
U [V] |
f [Hz] |
I [A] |
UR [V] |
UL [V] |
UC [V] |
f0mas [Hz] |
Q
|
Obs |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tabelul 1
Tabelul 2
|
Nr. crt. |
R Ω |
L H |
C F |
f0calc Hz |
BLr Ω-1 |
BCr Ω -1] |
U [V] |
f [Hz] |
I [A] |
IR [A] |
UL [V] |
f0mas [Hz] |
Q |
Obs |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|