
|
|
|
STABILITATEA MEMORIEI ASOCIATIVE BIDIRECTIONALE
1. Stabilitatea bidirectionala
Diferite modele de schimbare asincrona a starilor nu conduc, in general, la acelasi punct de echilibru, insa ele tind sa produca acelasi echilibru. De asemenea, °onditii initiale apropiate tind sa convearga spre acelasi punct de echilibru, tendinta °are se atenueaza cu distanta. Aceasta comportare evidentiaza proprietatea de
memorieadresabila prin continut aretelelor detipulmemorieiasociative bidirectionale.
in cazul unei memorii asociative bidirectionale, vectorii x si y se schimba in4 functie de timp, formand un sistem dinamic. Studiul acestui sistem dinamic poate furniza raspunsuri la intrebarile urmatoare:
(i) exista o solutie a problemei de instruire ?
(ii) daca solutia exista, va converge sistemul spre aceasta solutie intr-un timp finit ?
Fie (Fx, Fy, W, I, J, U, V) un sistem MAB general. Spunem ca acest sistem este bidirectional stabil (bistabil), daca orice intrare conduce la un echilibru de punct fix. Stabilitatea bidirectionala astfel definita este un exemplu de stabilitate globala sau absoluta. Aceasta stabilitate reprezinta un echilibru dinamic. Acelasi semnal informational parcurge reteaua inainte si inapoi, realizand un punct l/x bidirectional (bipolar).
Fie x intrarea unei memorii asociative bidirectionale. Putem reprezenta
modul in care aceasta memorie se echilibreaza la punctul fix bidirectional (x*, y*) prin urmatoarea schema:
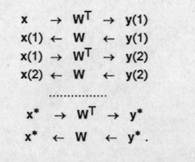
2. Consideratii elementare privind functiile Liapunov
Metoda functiilor Liapunov reprezinta un instrument puternic in studiul stabilitatii globale a sistemelor dinamice. Daca putem asocia sistemului o astfel de functie, atunci el este stabil. in caz contrar, nu se poate afirma nimic despre stabilitatea sa. Aceasta abordare este pur calitativa: ea indica doar existenta punctelor de echilibru, dar nu si numarul, pozitia sau natura lor.
in cazul memoriei asociative bidirectionale, stabilitatea asigura ca o regasire a informatiei are loc atunci cand retelei i se prezinta un stimul (o forma) de intrare, fara a sti, insa, care vector anume va fi regasit. Aceeasi problema apare si in cazul retelelor neuronale utilizate pentru rezolvarea problemelor de optimizare
combinatoriala. In cazul din urma, stabilitatea implica doar faptul ca reteaua va atinge un punct de echilibru asociat unui minim local al functiei criteriu asociata problemei de optimizare combinatoriala.
O functie Liapunov este o functie de variabilele de stare ale sistemului, marginita si descrescatoare in raport cu timpul.
in cazul memoriei asociative bidirectionale, o functie Liapunov este o functie L ,
![]()
unde Bn este cubul n-dimensional boolean n sau cubul bipolar n. Evident, L satisface conditiile de marginire si monotonie. Admitem ca fiecare variabila x,- a functiei L depinde de parametrul timp.
Fie L : R' -> R o functie Liapunov. Consideram ca L este derivabila in raport cu toate variabilele si ca toate variabilele sunt derivabile in raport cu timpul. Putem, deci, scrie
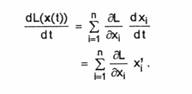
Am notat cu Xj derivata in raport cu timpul a variabilei x,-.
3. Exemple de functii Liapunov
Consideram un sistem dinamic avand variabilele de stare jt,, x2, ,xn si presupunem ca el evolueaza dupa legea
![]() (D Aceasta
ecuatie diferentiala liniara are solutia
(D Aceasta
ecuatie diferentiala liniara are solutia
![]()
deci sistemul tinde exponential spre origine. Sistemului ii asociem functia patratica
|
|
avand expresia
|
|
Am notat cu x vectorul variabilelor de stare:
![]()
Functia L se mai poate scrie
![]()
unde E este matricea unitate (n x n). Derivata functiei L in raport cu timpul este
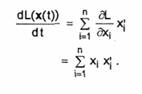
|
|
|
Rezulta ca vom avea
de-a lungul traiectoriei sistemului (L descreste cu timpul), atat timp cat cel putin una dintre variabilele de stare este nenula. Starea de echilibru L(x(t)) = 0 apare daca si numai daca toate derivatele variabilelor in raport cu timpul (vitezele) sunt zero: |
Conform legii de evolutie (1) obtinem
![]()
Exemplul considerat ilustreaza proprietatile esentiale ale functiilor Liapunov. in acest exemplu, originea este singurul punct de echilibru. Modificarea functiei L se opreste daca si numai daca vectorul de stare nu se mai schimba (isi opreste miscarea in spatiul starilor).
Sisteme dinamice stabile
Vectorul de stare x este o stare de echilibru daca
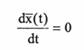
O stare de echilibru x este (uniform) stabila daca este indeplinita conditia
![]()
Aceasta definitie reliefeaza faptul ca traiectoria sistemului poate fi facuta sa ramana in vecinatatea starii de echilibru x daca starea initiala x(0) este suficient de apropiata de x.
O stare de echilibru xeste convergenta daca exista 5 > 0 astfel incat
![]()
Conform acestei definitii, daca starea initiala x(0) este destul de apropiata de x atunci traiectoria va converge spre x,
Stabilitatea si convergenta sunt proprietati independente. in cazul stabilitatii, traiectoria sistemului poate sa nu atinga punctul de echilibru ,
Starea de echilibru x este asimetric stabila daca x este o stare stabila si convergenta.
Se poate arata (vezi, de exemplu, Elbert, 1984) ca un sistem dinamic este intr-un echilibru stabil daca exista o functie Liapunov L care descreste de-a lungul traiectoriilor, adica
![]()
Un sistem dinamic este asimptotic stabil daca i se poate asocia o functie Liapunov care descreste strict de-a lungul traiectoriilor, adica avem
![]() 3
3
pentru orice traiectorie posibila a sistemului.
intr-un echilibru stabil, traiectoria poate sa oscileze arbitrar aproape de punctul de echilibru, fara a-l putea atinge. in cazul echilibrului asimptotic stabil, traiectoria atinge echilibrul si, in general, convergenta spre echilibru are o viteza exponentiala (Anderson si Moore, 1979),
Monotonia unei functii Liapunov reprezinta o conditie suficienta, dar nu si necesara, pentru stabilitate. Inabilitatea de a asocia sistemului o functie Liapunov nu ne permite sa tragem nici o concluzie privitoare la stabilitate, insa gasirea unei astfel de functii (de orice forma) demonstreaza stabilitatea. Din pacate, in afara functiilor patratice nu avem o procedura universala de generare a functiilor Liapunov.
Exemple.
Exemplul 1.
Functia Liapunov asociata sistemului liniar (1) satisface inegalitatea
![]()
Rezulta ca acest sistem este asimptotic stabil.
Exemplul 2.
Vom considera un exemplu mai general decat (1). Fie sistemul dinamic liniar avand ecuatia de evolutie
![]() (3)
(3)
unde B este o matrice patratica (n x n). Asociem acestui sistem functia
L:R'->R
avand expresia
|
|
L(x) = xT A x ,
unde A este o matrice simetrica. Functia L poate fi o functie Liapunov strict descrescatoare pentru sistemul considerat, daca matricile A si B satisfac o anumita relatie. Astfel, avem
Deoarece![]()
![]()
obtinem ca
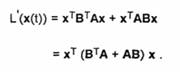
Rezulta ca L este o functie Liapunov strict descrescatoare daca si numai daca matricea
![]()
este negativ definita. in acest caz, avem
![]()
deci sistemul liniar (3) este asimptotic stabil.
5. Functia energie pentru retele neuronale
Energia unui sistem fizic poate fi deseori interpretata drept o functie Liapunov a sistemului. Prin analogie cu un sistem fizic, se poate defini energia unei retele neuronale, lucru efectuat de Hopfield (1982). O forma patratica depinzand de variabilele de stare ale sistemului (sau de viteze) poate fi considerata ca fiind energia potentiala (sau cinetica) a sistemului.
Sa consideram un sistem fizic de n variabile si fie £ energia sa potentiala. Coordonata x, se va interpreta ca deplasarea fata de echilibru a particulei i, apartinand sistemului. Originea este, asadar, un punct de echilibru in raport cu
energia potentiala. Putem admite ca energia potentiala in origine este zero. Energia potentiala £ depinde doar de coordonate:
![]()
Presupunem ca E admite o dezvoltare in serie Taylor in jurul originii. Putem deci scrie
|
|
unde derivatele sunt luate intr-un punct dintr-o vecinatate a originii. Pentru deplasari mici, termenii de ordin superior pot fi neglijati.
Originea este un punct de echilibru doar daca ea este un punct de minimal energiei. in acest caz, in orice vecinatate a originii avem
![]()
Neglijand termenii de ordin superior si tinand cont de conditia
![]()
|
|
obtinem, pentru energia potentiala, aproximatia
Notam
![]()
Matricea A cu elementele A;j este simetrica. Aproximatia energiei se poate acum scrie
![]()
Am obtinut, astfel, o aproximatie a energiei care are forma functiei Liapunov considerata in sectiunea precedenta. Asadar, functia
![]()
avand expresia
![]()
poate fi considerata o functie Liapunov utila in studiul echilibrului retelelor neuronale. Aceasta functie are semnificatia unei energii.
Am vazut ca o functie ce candideaza pentru alegerea ca functie Liapunov a unui sistem trebuie sa fie descrescatoare si marginita. Formele patratice considerate mai sus pot creste nemarginit (in valoare absoluta) cu cresterea variabilelor de stare. Din acest motiv, folosim ca variabile de stare nu activarile neuronale, ci semnalele de iesire neliniare ale neuronilor (a caror valoare maxima este, de regula, egala cu unu).
Functiile Liapunov permit descrierea comportarii globale a retelelor neuronale. Pe masura ce valoarea functiei Liapunov asociate descreste, sistemul trece prin stari tranzitorii. Punctul pentru care descresterea inceteaza corespunde echilibrului sistemului. Acest punct poate sa corespunda terminarii procesului de instruire.
Daca functia Liapunov este asociata unei memorii asociative bidirectionale, atunci punctul de echilibru corespunde regasirii unei informatii (forme). Daca reteaua rezolva o problema de optimizare combinatoriala, atunci punctul de echilibru indica solutia problemei (un punct de optim al functiei criteriu asociate problemei).
6. Stabilitatea memoriei asociative bidirectionale
Pentru studiul stabilitatii memoriei asociative bidirectionale, vom considera diferite functii Liapunov de tip energie. Stabilirea acestor functii depinde de complexitatea retelei. Luam, pentru inceput, cazul standard, in care pragul fiecarui neuron este zero si intrarile din mediu sunt nule, adica :
![]()
Si
![]()
Acest model de memorie asociativa se noteaza cu (Fx, Fy, W). Pentru el putem construi o functie Liapunov simpla. Considerand starile neuronilor bipolare (-1 si 1), definim functia de energie
![]()
unde W este matricea ponderilor retelei.
Functia energie considerata se mai scrie sub forma
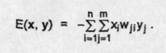
Dorim sa aratam ca £ se comporta ca o functie Liapunov. Aceasta presupune sa demonstram ca energia descreste de-a lungul traiectoriilor reprezentate de starile discrete ale retelei. Descresterea are loc pentru orice schimbari (sincrone sau asincrone) ale starilor. Urmatoarea teorema privind functia de energie ne ajuta sa obtinem un raspuns referitor la existenta starilor stabile ale memoriei asociative bidirectionale.
Teorema MAR. Pentru orice memorie asociativa bidirectionala asociata modelului (Fx, Fy, W) sunt adevarate urmatoarele afirmatii :
(i)Orice schimbare a vectorilor de stare x si y in timpul functionarii retelei produce o descrestere a functiei £, ce reprezinta energia retelei, 'unde
![]()
)Functia energie este marginita. Valoarea minima a energiei este
![]()
(iii) Energia variaza in cantitati discrete. Variatia energiei nu poate fi niciodata arbitrar de mica (nu exista nici o schimbare a starii neuronilor pentru care energia sa fie oricat de mica).
Demonstratie.
(i) Presupunem ca cel putin un neuron isi schimba starea de la momentul t la (t+1), ceea ce ne permite sa adoptam orice strategie de actualizare (sincrona, asincrona sau simplu asincrona). Consideram ca neuronul r din stratul Fy si-a schimbat starea. Pentru a calcula variatia energiei produsa de aceasta schimbare, energia retelei va fi scrisa sub forma
|
|
Fie y'r noua stare a neuronului r si E' energia corespunzatoare. Energia E se poate scrie
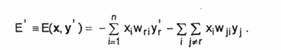
Variatia AE a energiei este
AE = E' -E
.n
(yr-yr)Ix.wri
i=1 = (yr-Yr)Rr-
Pentru a gasi semnul acestei variatii, consideram cele trei situatii posibile :
(a)![]()
Cazul y'r = -1 se obtine daca activarea neuronului r este negativa, adica
![]()
Cum yr - y'r > 0, rezulta imediat ca avem AE < 0.
(b) yr = -i.yr=i-
Tranzitia corespunzatoare acestui caz se poate realiza numai daca activarea este strict pozitiva (Rr > 0), Acum, yr - y'r< o si deci, din nou AE<0.
![]()
(c)yr = yr-
Rezulta AE = 0.
Am obtinut ca in orice situatie avem AE < 0.
Consideram cazul general cand se schimba simultan starea mai multor neuroni. Acum variatia energiei este
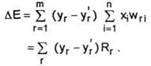
Cum fiecare dintre cei m termeni din aceasta suma este negativ sau zero, rezulta ca energia descreste.
Schimbarea starilor pentru stratul Fx se trateaza analog.
(i/) Deoarece x, si yy- iau doar valorile 1 si -1, rezulta ca £ este marginita superior. Din inegalitatea
![]()
rezulta ca
![]()
Cum ponderile conexiunilor sunt finite, rezulta ca functia energie este marginita. Se observa imediat ca energia poate atinge valoarea minima
![]()
(iii) Tinand cont de forma variatiei energiei, rezulta ca aceasta nu poate fi arbitrar de mica. La orice schimbare a starii neuronilor, energia inregistreaza un salt discret
7. Stabilitatea memoriei asociative bidirectionale. Cazul general
Fie (Fx, Fy, W, I, J, U, V) un sistem MAB general. Este natural ca energia acestui sistem sa inglobeze si pragurile neuronilor, precum si intrarile exterioare. Acestea din urma apar in expresia activarii. Energia asociata starii (x, y) a retelei se defineste cu expresia
![]()
unde am notat
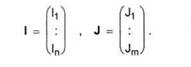
U si V sunt vectori avand drept componente pragurile neuronilor, adica
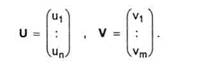
Energia E se poate scrie
![]()
Vom arata ca aceasta energie reprezinta o functie Liapunov pentru memoria asociativa bidirectionala considerata.
Variatia energiei datorita schimbarii starii neuronilor din campul Fx este
|
|
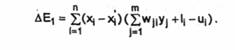
Analog, variatia energiei la schimbarea starii neuronilor din stratul Fy va fi
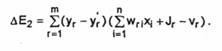
Expresiile pentru AE< si AE2 sunt valabile atat pentru un model de activare sincron, cat si pentru o activare asincrona. in cazul modelului asincron, acei neuroni / din Fx ce nu-si modifica starea sunt caracterizati de x'| = xv O situatie similara are loc si pentru campul Fy .
Din expresia variatiei energiei, se deduce imediat ca inegalitatea
![]()
are loc pentru orice schimbare a starii retelei.
Pentru determinarea marginii inferioare si superioare a energiei, o vom scrie sub forma
![]()
unde am utilizat produsul scalar
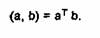
Tinand cont de inegalitatea Cauchy - Schwartz
![]()
obtinem ca, pentru orice stare (x, y), avem
|
|
(I - U, x) <; j I - U | | x |
Deoarece x, este -1 sau 1, rezulta ca
R V
Si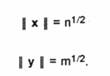
Rezulta, astfel, ca energia satisface inegalitatea
![]()
Aceasta inegalitate se mai poate scrie sub forma
![]()
Am gasit, asadar, o margine inferioara a energiei.
Similar, se arata ca energia este marginita si superior. in concluzie, rezulta ca energia introdusa este o functie Liapunov pentru o memorie asociativa bidirectionala generalizata.
8. Consecintele teoremei de stabilitate a memoriei asociative bidirectionale
8.1. Evolutia retelei spre stari de minim local ale energiei
Afirmatiile (i) si (ii) din Teorema de stabilitate a memoriei asociative bidirectionale demonstreaza ca energia este o functie Liapunov. Asadar, sistemul MAB are o stare stabila. Deoarece exista o valoare minima a energiei (afirmatia (ii) din teorema), rezulta ca energia nu poate descreste indefinit. Cum energia variaza 'n cantitati discrete (afirmatia (iii)), rezulta ca descresterea energiei la un pas nu poate fi arbitrar de mica.
Asadar, din afirmatiile (ii) si (iii) ale Teoremei MAB rezulta ca un minim al energiei (punct de echilibru) este atins intr-un numar finit de iteratii.
Forma suprafetei generate de functia de energie este determinata de matricea W a ponderilor. Starea initiala a sistemului este data de vectorii de stare
x si y initiali. Functionarea retelei determina schimbarea acestor vectori. Aceasta schimbare provoaca o deplasare in spatiul starilor sistemului, urmand suprafata functiei de energie. Teorema MAB ne garanteaza ca miscarea are loc intotdeauna in sensul descresterii energiei. Energia descreste odata cu apropierea vectorilor x si y de starea lor stabila. Schimbarea energiei inceteaza cand se atinge un punct de minim local al energiei. Minimul local depinde de starea initiala a sistemului.
8.2. Regasirea de ordinul intai
Problema este daca fiecare minim local corespunde unei forme memorate, in tehnicile de codificare bazate pe corelatie (cum este si cea folosita in cazul memoriei asociative bidirectionale), informatia memorata tinde sa ocupe puncte corespunzand minimelor locale ale functiei de energie. Rezulta, astfel, o proprietate importanta a acestor memorii. Timpul necesar retelei sa ajunga intr-un minim local, adica timpul de regasire a unei informatii, nu depinde de numarul p al formelor memorate. Aceasta proprietate exprima independenta fata de dimensiune a procesului de regasire. Acest tip de regasire se mai numeste si regasire de ordinul 1 (regasire 0(1)).
Regasirea de tipul 0(1) nu este specifica doar pentru memoria asociativa bidirectionala, ci caracterizeaza toate retelele neuronale stabile. Acest lucru sugereaza existenta unui mecanism distribuit si in cazul sistemelor biologice de recunoastere a formelor (sisteme care lucreaza in timp real). Cercetari recente in biologie tind sa confirme aceasta ipoteza. Procesele biologice de recunoastere, ca si memoria, nu sunt strict localizate (in cortex). Ele sunt, mai degraba, distribuite peste numeroase, eventual peste toate celulele nervoase.
Acuratetea recunoasterii (clasificarii obiectelor) poate sa se schimbe cu timpul. Numarul de informatii aflate in memorie la fiecare moment este variabil. Supraincarcarea memoriei poate sa duca la o degradare a acuratetei in regasirea informatiilor. Forme similare memorate pot avea domenii (minime locale sau "bazine de atractie') care se suprapun. in plus, pot aparea bazine de atractie false. Aceste situatii pot genera ambiguitati in procesul de recunoastere (regasire a informatiei). Ele nu afecteaza insa, in mod esential, viteza de recunoastere (clasificare), care ramane aproximativ constanta.
Regasirea de tipul 0(1) este un avantaj important al sistemelor dinamice neuronale fata de calculatoarele numerice, secventiale sau paralele, pentru care timpul de cautare creste cu numarul de entitati memorate. in prezent, sistemele bazate pe calcul neuronal se dovedesc a fi mai eficiente in recunoasterea formelor de dimensiuni mari, imprecis definite sau distorsionate. in plus, ele nu necesita cunoasterea si programarea algoritmului care realizeaza o anumita functie, ci il "sintetizeaza' din exemplele de instruire. Din acest motiv, retelele neuronale pot fi considerate masini inteligente, capabile sa foloseasca algoritmi de recunoastere "opaci', de felul celor folositi de fiintele superioare.
8.3. Rapiditatea convergentei
Am stabilit ca traiectoriile MAB converg spre atractori de punct fix (puncte de minim local ale energiei). Putem studia rapiditatea acestei convergente examinand descresterea functiei Liapunov odata cu schimbarea starilor neuronilor.
Am vazut ca variatia energiei este
|
|
si, respectiv
![]()
Asadar, descresterea energiei este egala cu suma descresterilor separate provocate de fiecare neuron din campurile Fx sau Fy care isi schimba starea. Aceasta constatare conduce la doua concluzii referitoare la convergenta memoriilor asociative bidirectionale spre cel mai apropiat minim local.
(I) Energiile individuale descresc in cantitatile discrete (Ayr)Rr sau (Axk)Sk. Rezulta ca energia totala nu poate descreste arbitrar de incet spre cel mai apropiat minim Liapunov. Asadar, sistemul va efectua salturi definite in bazinul de atractie al punctului de echilibru si, in final, va atinge punctul de echilibru.
(ii) Memoriile asociative bidirectionale sincrone converg mai rapid decat cele asincrone. Functia Liapunov descreste iar viteza de convergenta creste cu numarul neuronilor ce se schimba la o iteratie. in mod uzual, retelele sincrone converg in doua sau trei iteratii, ceea ce asigura o regasire cvasiinstantanee a informatiei.
Chiar daca rezultatele de mai sus se refera, mai ales, la memoria asociativa bidirectionala de forma (Fx, Fy, W), aceste concluzii pot fi usor extinse pentru modelul general.