
|
|
|
Sisteme numerice
Introducere
1 Sistem numeric zecimal
2 Sistem numeric binar
3 Sistem numeric hexazecimal
Concluzie
Introducere
A fost dificil pentru oameni sa accepte faptul ca unele lucruri difera de ei si de modul lor de gandire. Acesta este probabil unul din motivele pentru care sistemele numerice care difera de cele zecimale sunt inca greu de inteles. Totusi, fie ca le vrem ori nu, realitatea este diferita. Sistemul numeric zecimal pe care oamenii il folosesc in viata de fiecare zi este de departe in urma sistemului binar folosit de milioane de calculatoare in lumea intreaga.
Fiecare sistem numeric se bazeaza pe o fundatie. La un sistem numeric zecimal, baza este 10, la binar 2, si la sistemul hexazecimal 16. Valoarea fiecarui zecimal este determinata de pozitia lui in relatie cu intreg numarul reprezentat in sistemul numeric dat. Suma valorilor fiecarui zecimal da valoarea intregului numar. Sistemele binare si hexazecimale sunt in special interesante pentru subiectul acestei carti. In afara de acestea vom discuta de asemenea un sistem zecimal, pentru a-l compara cu celelalte doua. Chiar daca un sistem numeric zecimal este un subiect cu care suntem bine familiarizati, il vom discuta aici din cauza legaturii sale cu alte sisteme numerice.
1 Sistem numeric zecimal
Sistemul numeric zecimal este definit de baza lui 10 si
de spatiul zecimal care este numarat de la dreapta la stanga, si
consta din numerele 1, 2, 3, 4, 5, 6, 7, 8, 9. Aceasta inseamna
ca numarul din capatul din stanga a sumei totale este
multiplicat cu 1, urmatorul cu 10, urmatorul cu 100, etc.
Exemplu:
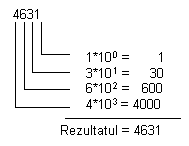
Operatiile de adunare, scadere, impartire si inmultire intr-un sistem numeric zecimal sunt folosite intr-un fel care ne este deja cunoscut, asa ca nu-l vom discuta mai departe.
2 Sistem numeric binar
Sistemele numerice binare difera in multe aspecte de
sistemul zecimal pe care il folosim in viata de zi cu zi. Baza lui
numerica este 2, si fiecare numar poate avea doar doua
valori, '1' sau '0'. Sistemul numeric binar este folosit in calculatoare
si microcontrolere pentru ca este de departe mai potrivit pentru
procesare decat un sistem zecimal. Uzual, numarul binar consta din
numerele 8, 16, sau 32, si nu este important avand in vedere
continutul de a discuta de ce. Este destul acum de a accepta aceasta
informatie.
Exemplu:
10011011 numar binar cu 8 digiti
Pentru a intelege logica numerelor binare, vom considera un exemplu. Sa spunem ca avem un mic dulapior cu patru sertare, si ca trebuie sa spunem cuiva sa ne aduca ceva din unul din sertare. Nimic nu este mai simplu, vom spune partea stanga, jos (sertarul), si sertarul dorit este clar definit. Totusi, daca ar fi trebuit sa facem aceasta fara folosirea instructiunilor ca stanga, dreapta, jos, sus, etc., atunci am fi avut o problema. Sunt multe solutii la aceasta problema, dar noi ar trebui sa cautam una care este cea mai benefica si practica! Sa desemnam randurile cu A, si tipurile cu Daca A=1, se refera la randul de sus a sertarelor, si pentru A=0, randul de jos. Similar cu coloanele, B=1 reprezinta coloana stanga, si B=0, dreapta (urmatoarea imagine). Acum este deja mult mai usor de a explica din care sertar avem nevoie de ceva. Trebuie doar sa formulam una din cel patru combinatii: 00, 01, 10 sau 11. Aceasta caracteristica denumind fiecare sertar individual nu este decat reprezentarea numerica binara, sau conversia numerelor comune dintr-o forma zecimala intr-una binara. Cu alte cuvinte, referirile ca 'primul, al doilea, al treilea si al patrulea' sunt schimbate cu '00, 01, 10 si 11'.
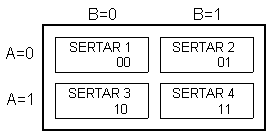
Ceea ce ne
ramane este sa ne acomodam cu logica care este folosita la
sistemul numeric binar, sau cu cum sa obtinem o valoare numerica
dintr-o serie de zero-uri si unu-uri intr-un fel in care sa-l
intelegem, bineinteles. Aceasta procedura se numeste
conversia dintr-un numar binar intr-unul zecimal.
Exemplu:
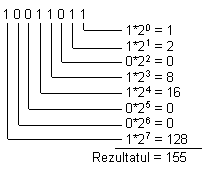
Dupa cum puteti vedea, convertirea unui numar
binar intr-unul zecimal se face prin calcularea expresiei din partea
stanga. Depinzand de pozitie intr-un numar binar, cifrele
poarta diferite valori care sunt multiplicate cu ele insele, si prin
adaugarea lor obtinem un numar zecimal pe care il putem
intelege. Sa presupunem mai departe ca in fiecare sertar sunt
cateva bile: 2 in primul, 4 in al doilea sertar, 7 in al treilea si 3 in
al patrulea sertar. Sa spunem de asemenea celui care deschide sertarele
sa foloseasca reprezentarea binara ca raspuns. In aceste
conditii, intrebarea ar fi: 'Cate bile sunt in 01?', si
raspunsul va fi: 'Sunt 100 de bile in 01.' Trebuie remarcat
ca atat intrebarea cat si raspusul sun foarte clare chiar
daca nu am folosit nume standard. Trebuie mai departe de observat ca
pentru numerele zecimale de la 0 la 3 este suficient de a avea doua cifre
binare, si ca pentru toate valorile de mai sus trebuie sa
adaugam cifre binare noi. Asa ca, pentru numere de la 0 la7
este suficient sa avem trei cifre, pentru numere de la 0 la 15, patru,
etc. Mai simplu spus, cel mai mare numar ce poate fi reprezentat de o
cifra binara este cel obtinut cand baza 2 este
gradata cu un numar de cifre binare intr-un numar binar
si astfel numarul derivat este decrementat cu unu.
Exemplu:
![]()
Aceasta inseamna ca este posibil de a se reprezenta numere zecimale de la 0 la 15 cu 4 cifre binare, incluzand numerele '0' si '15', sau 16 valori diferite.
Operatiile ce exista in sistemul numeric zecimal exista de asemenea intr-un sistem binar. Din motive de claritate si descifrabilitate, vom revedea adunarea si scaderea doar in acest capitol. Regulile de baza care se aplica adunarii binare sunt:
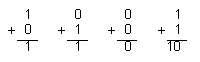
Adunarea se face asa incat cifrele din aceeasi
pozitie nmerica sunt adunate, similar sistemuluii numeric
zecimal. Daca ambii digiti de adunat sunt zero, suma lor ramane
zero, si daca sunt '0' si '1', rezultatul este '1'. Suma a doi
de unu da zero, dar cu transferarea unui '1' la pozitia de mai sus
care este adunat cifrelor din acea pozitie.
Exemplu:

Putem verifica
daca rezultatul este corect transferand aceste numere in sistemul numeric
zecimal si facand adunarea in el. La transfer obtinem valoarea
10 ca primul numar, valoarea 9 ca al doilea, si valoarea 19 ca
suma. Astfel am dovedit ca operatia s-a facut corect.
Probleme apar cand suma este mai mare decat ceea ce poate fi reprezentat de un
numar binar cu un numar dat de cifre binare. Se pot aplica diferite
solutii atunci, una este sa crestem numarul de cifre binare
in suma ca in exemplul anterior. Scaderea, ca
si adunarea se face pe acelasi principiu. Rezultatul scaderii
dintre doi de zero, sau doi de unu ramane zero. Cand scadem unu din
zero, trebuie sa imprumutam unu de la cifra binara care este pe
o pozitie mai sus in numarul binar.
Exemplu:

Verificand rezulatul cum am facut si cu adunarea, cand translam aceste numere binare obtinem numerele zecimale 10 si 9. Diferenta lor corespunde numarului 1 care este ceea ce obtinem din scadere.
3 Sistem numeric hexazecimal
Sistemul numeric hexazecimal are numarul 16 ca
baza a sa. Pentu ca baza unui sistem numeric este 16, sunt 16 cifre
care se pot gasi intr-un numar hexazecimal. Aceste cifre sunt
'0, 1, 2, 3, 4, 5, 6, 7, 8,
Exempul:
![]()
Uzual, numarul hexazecimal este scris cu un semn
'$' sau '0x' inanitea lui, pentru a evidentia sistemul
numeric. Astfel, numarul A37E ar fi scris mult mai corect ca $A37E sau
0xA37E. Pentru a transla un numar hexazecimal intr-un sistem numeric
binar nu este necesar de a face nici un calcul ci simpla schimbare de cifre
hexazecimale cu cifre binare. Pentru ca valoarea maxima a
numarului hexazecimal este 15, aceasta inseamna ca este
suficient sa se foloseasca 4 cifre binare pentru o cifra hexazecimala.
Exempul:
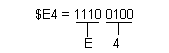
Veificand, sau
transferand ambele numere intr-un sistem numeric zecimal, obtinem
numarul 228 ceea ce dovedeste acuratetea actiunii noastre.
Pentru a obtine un zecimal echivalent a unui numar hexazecimal,
trebuie sa inmultim fiecare cifra a unui numar cu
numarul 16 care este gradat prin pozitia acelei cifre in
numarul hexazecimal.
Exempul:
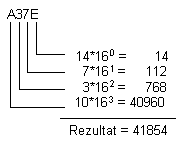
Adunarea, ca
si in precedetele doua exemple, se face intr-o maniera
similara.
Exempul:

Trebuie sa adaugam cifrele
corespunzatoare ale numarului; si, daca suma lor este mai
mare ca 16, trebie sa scriem numarul '0' acolo. Valoarea peste 16
trebuie adunata urmatoarelor doua cifre mai mari in valoare.
Verificand, obtinem 14891 ca prim numar, si al doilea este
43457. Suma lor este 58348, care este numarul $E3EC cand este
transferat in sistemul numeric zecimal. Scaderea este un proces identic
celor doua sisteme numerice anterioare. Daca numarul pe care il
scadem este mai mic, imprumutam din urmatorul loc al valorii mai
mari.
Exemplu:

Verificand rezultatul, obtinem valorile 11590 pentru prmul numar si 5970 pentru al doilea, cand diferenta lor este 5620, ceea ce coresponde numarului $15F4 dupa transferul intr-un sistem numeric zecimal.
Concluzie
Sistemul numeric binar este inca cel mai folosit, cel zecimal cel mai usor de inteles, iar cel hexazecimal este intre cele doua sisteme. Conversia lui usoara intr-un sistem numeric binar si memorarea lui usoara il fac, impreuna cu sistemele binar si zecimal, unul din cele mai importante sisteme numerice.