
|
|
|
ALTE MODELE DE MEMORII ASOCIATIVE BIDIRECTIONALE
1. Memorii asociative bidirectionale adaptive
Modelele de memorii asociative bidirectionale considerate calculeaza, in mod simplu, matricea W a conexiunilor ca suma matricelor de corelatie asociate formelor de instruire. Sisteme mai evoluate, bazate pe actualizarea iterativa a ponderilor, permit o convergenta mai rapida sau o regasire mai corecta.
Un mecanism iterativ de antrenare a memoriilor asociative bidirectionale poate utiliza, de exemplu, legea de invatare a lui Hebb, scrisa sub forma
![]()
unde x,(t+1) este starea neuronului idin campul Fx la iteratia (t+f), iar Vj(t+1) este starea neuronului / din stratul Fy .
Alte legi de invatare care pot fi utilizate sunt invatarea competitiva (in care neuronii concureaza la .privilegiul' de a fi activati) sau invatarea Hebb diferentiala. Pentru oricare dintre metodele iterative de instruire ce pot fi astfel obtinute, se pune cu prioritate problema convergentei.
2. Memorii asociative bidirectionale
Principala dificultate a memoriilor asociative bidirectionale este legata de limitarea drastica a posibilitatilor de memorare. Capacitatea de regasire a asociatiilor descreste cu numarul formelor memorate, daca acest numar depaseste minimul dimensiunilor celor doi vectori. Capacitatea de memorare pentru care se obtin rezultate satisfacatoare este
![]()
Pentru forme de dimensiune mare, aceasta restrictie nu reprezinta o problema. Multe aplicatii practice implica, insa, forme de dimensiuni moderate. Pentru astfel de aplicatii, folosirea memoriilor asociative bidirectionale este serios limitata.
O cale de depasire a acestor dificultati a fost propusa de Simpson(1990). Abordarea sa, cunoscuta sub numele de sistem MAS sau sistem MAB multi-
fpatricial, implica utilizarea mai multor matrice. Cand capacitatea de memorare a unei matrice este saturata se considera o noua matrice. Fiecare matrice permite codificarea (memorarea) mai multor asociatii.
Codificarea unei forme in sisteme MAS muiti-matriciaie.
Perechile de forme sunt memorate pe rand, construind initial o singura matrice MAB a ponderilor. Fie Wt aceasta matrice initiala. Ea se determina ca suma matricelor de corelatie asociate perechilor considerate. Se testeaza W1 pentru a ne asigura ca fiecare pereche deja memorata poate fi regasita.
Daca o pereche de vectori (reprezentand o asociatie) nu este regasita, atunci perechea curenta (xi, yi) este indepartata din W, si se incearca memorarea ei in alta matrice W2. Daca prezenta perechii (xi, y)) provoaca o regasire incorecta a vreunei perechi deja memorate in W2, atunci se incearca memorarea sa intr-o matrice W3. Procesul continua pana cand se obtine o matrice Wj , astfel incat toate perechile de forme memorate in ea sa fie corect regasite. Asociatia (xi, yi) este atunci memorata permanent in aceasta ultima matrice.
Regasirea formelor in sistemele MAB multi-matriciale.
Regasirea inseamna, ca si in cazul memoriei asociative bidirectionale standard, doua lucruri :
(i)obtinerea formei yi, cand retelei i se prezinta forma asociata xi;
(iOgasirea unei forme y, apropiate de yi , cand retelei i se prezinta o forma x, apropiata de xi.
Deoarece asociatiile au fost memorate in diferite matrice, nu este sigur la care dintre aceste matrice trebuie apelat pentru regasire. Drept criteriu, se foloseste apropierea de energia unei MAB ortogonale.
Fie x forma prezentata retelei. Ca raspuns, se primeste o multime de forme.
Definim energia MAB ortogonale ca fiind energia asociata situatiei in care toate formele memorate sunt descrise de vectori ortogonali. Consideram ca ei au componentele -1 si 1,
Energia unei perechi (x, y) este energia retelei corespunzatoare starii (x, y):
![]()
Daca (xk, y*) este o pereche memorata, atunci energia E0 a unei MAB ortogonale este
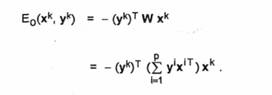
Din conditia de ortogonalitate avem
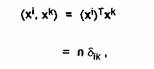
unde n este dimensiunea vectorilor - forma. Energia se poate acum scrie
|
|
E0(xk,yk) = -n(yf Zy^ i=i
= - n (y*)T yk . Rezulta, asadar, ca energia oricarei perechi (xk, yk) memorate este
![]()
unde m este dimensiunea vectorilor y.
Admitem ca se prezinta retelei o forma x. Ca raspuns, vom primi o multime de perechi de forme
![]()
Alegem din G acea pereche (x, y') a carei energie este cea mai apropiata de energia
|
|
E0 = - n m
a memoriei asociative bidirectionale ortogonale. Dintre formele multimii G le determinam pe acelea care au aceeasi energie ca perechea (x, y') selectata.
Sistemele MAB multi-matriciale pot fi folosite pentru recunoasterea cuvintelor rostite (formele produse de un analizor acustic sunt asociate cuvantului real), recunoasterea optica a caracterelor etc in general, retele de acest tip pot fi utilizate in aproape orice aplicatie in care avem un mare numar de asociatii ce trebuie regasite aproape instantaneu si unde ar putea fi utila o anumita toleranta fata de erori.
3. Memorii asociative bidirectionale multistrat
Extinderea arhitecturii memoriei asociative bidirectionale, permitand existenta straturilor ascunse, conduce la performante crescute, referitoare la eroarea de clasificare a formelor si la cea de regasire a informatiei.
in Figura 2 se prezinta o memorie asociativa bidirectionala cu trei straturi (doua ascunse), care poate fi interpretata ca un perceptron multistrat cu conexiuni de tip Hopfield intre straturile invecinate (Simpson 1990). Activarile optime ale neuronilor ascunsi sunt calculate adaptiv, pe baza minimizarii erorii patratice globale la iesire. Modelul poate fi generalizat relativ usor, la mai multe straturi ascunse.
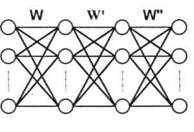
X hi h2 y
Figura 2. O memorie asociativa bidirectionala multistrat
Stratul de intrare, cele doua ascunse si cel de iesire sunt reprezentate
respectiv de vectorii x, h1, h2 si y. Fie multimea de
instruire. Initializand aleator activarile h1s si h2s , se determina matricele ponderilor cu regula Hebb, astfel :
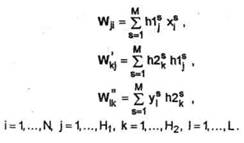
in relatiile de mai sus, N, H1t H2, si L reprezinta, respectiv numarul neuronilor stratului de intrare, al straturilor ascunse si al celui de iesire.
Fie St, S2 si S3 functiile sigmoidale aferente, respectiv, straturilor ascunse si celui de iesire. Notam
![]()
![]()
Cu aceste notatii, avem
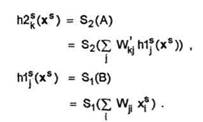
Eroarea globala la iesire se defineste ca
![]()
unde activarea neuronului ide iesire este
![]()
Minimizarea erorii E in raport cu activarile h1s si h2s se poate realiza folosind metoda gradientului. in acest fel, obtinem regulile de actualizare :
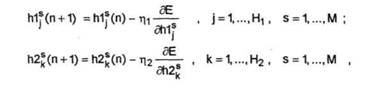
in care n este numarul iteratiei iar r^ si f2 sunt constante pozitive. Introducem notatiile
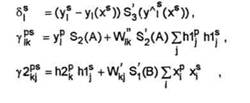
unde S i reprezinta derivata lui Sf.
Cu aceste notatii, derivatele anterioare se pot scrie
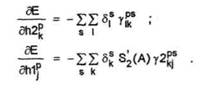
Memoriile asociative bidirectionale multistrat pretind pentru instruire un efort de calcul marit. Avantajul acestor memorii consta in cresterea capacitatii de memorare. De asemenea, corectia erorilor in comparatie cu retelele ce utilizeaza propagarea inapoi (un perceptron multistrat, de exemplu) este mai simpla.
CONCLUZII
Memoriile asociative bidirectionale (MAB) sunt memorii adresabile prin continut. Construirea de memorii adresabile prin continut reprezinta un deziderat vechi in stiinta calculatoarelor. Memoriile asociative bidirectionale realizeaza regasirea practic instantanee a asociatiilor de forme. in acelasi timp ele prezinta o buna toleranta la erori si la ambiguitate. in plus, aceste memorii sunt caracterizate de stabilitate globala.
Principalul neajuns al lor consta in limitarea numarului de asociatii ce pot fi memorate, numar inferior minimului dimensiunilor formelor. Pentru aplicatii in care dimensiunea vectorilor-forma este mica aceasta limitare constituie un dezavantaj major. Sistemele MAB multi-matriciale si multistrat par sa rezolve aceasta problema. Implementarea prin circuite VLSI a acestor sisteme asigura un timp de regasire satisfacator pentru numeroase aplicatii.
BIBLIOGRAFIE
[1] Amari, S., Neural Theory of Association and Concept Formation, Biological Cybemetics,26 (1977), 175-185.
[2] Anderson, J.A., A Simple Neural Network Generating an Associative Memory, Mathematical Biosciences, 14(1972), 197-220
[3] Anderson, B.D., Moore, J.B., Optimal Filtering, Prentice Hali, Englewood Cliffs, NJ, 1979
[4] Cohen, M.A., Grossberg, S.G., Absolute Stability of Global Pattern Formation and Parallel Memory Storage by Competitive Neural Networks, IEEE Trans. SMC 13(1983), 815-826
[5] Elbert, T.F., Estimation and Control of Systems, Van Nostrand, Reinhold, New York, 1984
[6] Grossberg, S.G., The Adaptive Brain (1, 2), North - Holland, Amsterdam, 1987
[7] Hopfield, J.J., Neural Networks and Physical Systems with Emergent Collective Computational Abilities, Proc. Natl. Acad. Sci., USA, 79(1982), 2554-2558
[8] Hopfield, J.J., Neurons with Graded Response have Collective Computational Properties Like those of Two-State Neurons, Proc. Natl. Acad. Sci., USA, 81(1984), 3088-3092.
[9] Kosko, B., Adaptive Bidirectional Associative Memories, Applied Optics, USA, 26(1987), 4947-4960