Mecanica sistemului de actionare electrica

MECANICA SISTEMULUI DE ACTIONARE ELECTRICA

Din prezentarea facuta in capitolul 1.2 rezulta ca numai trei sisteme din cadrul unui sistem de actionare electrica au elemente in miscare: convertorul electromecanic (CEM), convertorul mecanic (CM) si mecanismul productiv (MP) (figura 1.5.a).

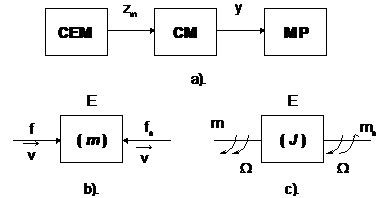
Fig. 1.5. Elementele in miscare ale unui SAE.

Convertorul electromecanic si mecanismul productiv pot executa fiecare o miscare de rotatie sau o miscare de translatie; corelarea dintre aceste miscari (eventual transformarea unui tip de miscare in celalalt) este realizata de catre convertorul mecanic. Rezulta ca ansamblul descris (CME + CM + MP) formeaza un agregat complex. Studiul miscarii acestui agregat complex consta in determinarea legilor de miscare a elementelor sale cunoscand legile de variatie ale fortelor, respectiv ale cuplurilor exterioare care se aplica agregatului.

1. Ecuatia generala de miscare

Miscarea efectuata de convertorul electromecanic (CEM) este caracterizata de parametrii z_m (figura 1.5.a) care pot fi: forta (f) si viteza (v) in cazul unei miscari rectilinii, respectiv cuplu (m) si viteza unghiulara () in cazul unei miscari circulare.

Analog, miscarea mecanismului productiv (MP) este caracterizata de parametrii y, care sunt similari cu parametrii convertorului electromecanic atunci cand se efectueaza acelasi tip de miscare. Evident, elementul activ al agregatului (CME+CM+MP) este convertorul electromecanic - CME - care produce forta sau cuplu.

Metoda utilizata pentru studiul miscarii agregatelor este metoda reducerii tuturor fortelor (cuplurilor) aplicate agregatului si a tuturor maselor elementelor agregatului la un singur element, la elementul redus. Prin aceasta metoda, problema dinamicii agregatului complex se inlocuieste cu problema miscarii unui singur element al sau. In cazul concret al unui sistem de actionare electrica, elementul la care se face reducerea este convertorul electromecanic - CEM. Astfel, agregatul complex descris in figura 1.5.a se reduce la un simplu element echivalent redus (E), care primeste forta activa (f), sau cuplul activ (m) de la CEM si asupra caruia actioneaza o forta rezistiva (f_s) - (figura 1.5.b) sau un cuplu rezistiv redus (m_s) - (figura 1.5.c) care modeleaza efectele mecanice ale convertorului mecanic CM si ale mecanismului productiv MP. Elementul echivalent are masa redusa m, respectiv momentul de inertie redus J.

Ecuatia de echilibru dinamic a elementului echivalent E este:

- pentru miscarea rectilinie (1.1.a)

- pentru miscarea de rotatie (1.1.b)

unde termenii:

              - reprezinta forta de inertie (1.2.a)

          - reprezinta cuplul dinamic (1.2.b)

Toate marimile din ecuatiile 1.1 pot lua atat valori pozitive, cat si valori negative.

In functionarea sistemelor de actionare electrica se disting doua regimuri de functionare: regimul stationar si regimul nestationar. In cadrul regimului stationar, parametrii cinematici si dinamici ai agregatului sunt constanti sau variaza dupa o lege periodica. Astfel, viteza elementului echivalent redus E este constanta sau variaza dupa o lege periodica.

Conditia de echilibru pentru cazul regimului static de functionare (v=ct. ; =ct.) este:

- pentru miscarea rectlinie (a)

- pentru miscarea de rotatie (b)

Deoarece in marea majoritate a cazurilor practice, convertorul electromecanic (CEM) este o masina electrica cu miscare de rotatie, in cele ce urmeaza, se va analiza numai cazul miscarii circulare, cazul miscarii rectilinii putand fi analizat intr-un mod similar.

Pentru cazul miscarii de rotatie, convertorul electromecanic (CEM) si ansamblul (CM + MP) se pot defini prin caracteristicile mecanice, caracteristica mecanica a masinii pentru CEM si caracteristica mecanica a sarcinii pentru ansamblul (CM + MP).

O caracteristica mecanica in regim static se defineste ca dependenta vitezei unghiulare de rotatie de marimea cuplului dezvoltat:

- caracteristica mecanica a masinii (1.4.a)

- caracteristica mecanica a sarcinii (1.4.b)

Conform conditiei (1.3), pentru un anumit sistem de actionare electrica, in regim static, punctul de functionare se obtine la intersectia dintre caracteristica mecanica a masinii si caracteristica mecanica a sarcinii (figura 1.6), unde punctul de functionare a fost notat cu A.

In figura 1.6, caracteristicile mecanice au fost considerate pana la o valoare maxima acceptabila pentru cuplu, numit cuplu maxim (M_m). Depasirea valorii M_m poate conduce in timp la o degradare rapida a unor parti componente ale masinii, datorate supraincalzirilor cauzate de pierderile exagerate de energie.

Din motive mecanice, nu poate fi depasita o viteza unghiulara maxima _m, impusa de convertorul electromecanic de catre sarcina (convertor mecanic plus mecanismul productiv) sau de catre procesul tehnologic. In consecinta, in planul caracteristicilor mecanice (m, ), se delimiteaza un domeniu admisibil de functionare - zona hasurata din figura 1.6. Punctul de functionare A, trebuie sa fie inclus in acest domeniu admisibil de functionare.

Caracteristicile mecanice se pot defini si in unitati relative:

(1.5.a)

(1.5.b)

             (1.5.c)

unde: _n este viteza unghiulara nominala, iar M_n si M_ns sunt cuplul nominal al masinii si respectiv al sarcinii;  este viteza unghiulara in unitati relative,  cuplul relativ activ (dezvoltat de masina electrica), respectiv _s este cuplul relativ de sarcina.

Pentru ca regimul static de functionare, caracterizat de punctul A, sa corespunda pentru toate elementele agregatului, este necesar ca punctul A sa fie in interiorul domeniului admisibil de functionare. Altfel, va trebui aleasa o alta masina electrica de antrenare, daca ansamblul convertor mecanic + mecanism productiv se doreste a fi pastrat in structura sa initiala.

Fig. 1.6. Punctul de functionare in regim static al unui SAE.

2. Componentele cuplului de sarcina

Cuplul de sarcina este format din urmatoarele componente:

1.   Cuplul datorat frecarilor este prezent atat la arborele motorului, cat si la alte parti componente ale sistemului de actionare. Cu m_F se noteaza cuplul de frecare total, raportat la arborele motorului;

2.   Cuplul datorat rezistentei aerului apare odata cu invartirea motorului si este notat m_ra

3.   Cuplul de sarcina, notat cu m_s, este cel cerut de catre sarcina si poate fi constant (sarcini potentiale), proportional cu patratul vitezei (ventilatoare) sau poate varia odata cu schimbarea modului de operare al sarcinii.

a)                           b)

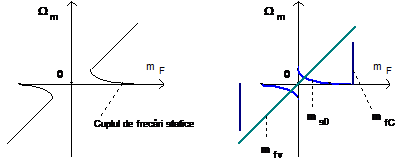
Fig. 1.7. Cuplul datorat frecarilor si componentele sale.

unde:

m_fv cuplul de frecari vascoase, proportional cu viteza;

m_fC cuplul de frecare coulombiana, independent de viteza;

m_s0 cuplul de frecare aditional, care este prezent numai in starea de repaus (sau viteze foarte mici);

m_ra cuplul datorat rezistentei aerului, proportional cu patratul vitezei.

Modul de variatie al cuplului de frecare este prezentat in figura 1.7.a. Valoarea sa la viteza zero, m_s0, este superioara valorii corespunzatoare la viteza putin peste zero. Componentele acestui cuplu sunt prezentate in figura 1.7.b.

Pentru regimul static de functionare, cuplul total al sarcinii este m_Stot

           (1.6.a)

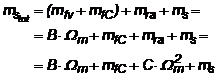                         (1.6.b)

Dar, in cele mai multe cazuri, cuplul de frecari coulombiene si cel datorat rezistentei aerului sunt mult mai mici decat cuplul de frecari vascoase si neglijabile fata de cel cerut de catre sarcina:

(1.7.a)

                       (1.7.b)

     (1.8)

Daca cuplul dezvoltat de catre masina m si cel cerut de sarcina m_S, nu sunt constante in timp, atunci ecuatia 1.8 este o ecuatie diferentiala neliniara, ce poate fi rezolvata numai numeric. Expresia cea mai des utilizata pentru ecuatia cuplului este cea din relatia 1.9, in care este neglijat si cuplul de frecari vascoase:

                    (1.9)

3. Exemple de cupluri de sarcina

Inainte de a analiza functionarea si stabilitatea in functionare a unui sistem de actionare electrica, este util a se cunoaste caracteristica mecanica viteza - cuplu a sarcinii. In figura 1.8 sunt prezentate cateva exemple de astfel de caracteristici.

Pentru pompe, suflante, ventilatoare si alte sarcini ce implica curgeri de fluide, cuplul variaza proportional cu patratul vitezei (figura 1.8.a). In cazul sistemelor de tractiune, trenuri electrice si autovehicule, neglijand cuplul datorat fenomenului de gravitatie, variatia cuplului cu viteza este prezentata in figura 1.8.b.

Printr-o analiza atenta a caracteristicii sarcinii, coroborata cu programul de lucru al acesteia, se pot lua decizii importante privind imbunatatirea parametrilor regimului tranzitoriu sau al celui permanent, obtinand rezultatele dorite. Spre exemplu, in cazul trenurilor, care au o masa apreciabila, cuplul de accelerare reprezinta un procent important din cuplul total.

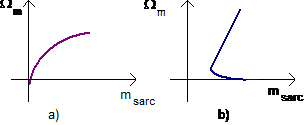
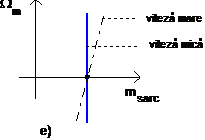
Fig. 1.8. Exemple de cupluri de sarcina.

Daca tinem cont de coeficientul de frecare care este definit ca raportul dintre forta de tractiune si masa rotilor motoare, se poate observa ca putem reduce timpul de accelerare printr-o crestere a masei acestora. Dar, nu trebuie uitat si faptul, ca acest coeficient mai depinde si de natura suprafetei de rulare si de alte conditii. Totusi, este de remarcat faptul ca o crestere a masei rotilor motoare poate duce la imbunatatirea timpului de accelerare. La trenurile ce parcurg de regula distante mari intre statii, valoarea maxima a greutatii rotilor motoare se aproximeaza la jumatate din greutatea locomotivei. In cazul metrourilor, acolo unde statiile sunt dese si se doreste in acelasi timp si obtinerea unor viteze medii satisfacatoare, se practica solutia cu vagoane motorizate. Astfel, greutatea totala a rotilor motoare a crescut foarte mult, putandu-se obtine acceleratii net superioare cazului anterior. Practica a aratat ca o solutie acceptabila este folosirea unui numar de roti motrice egal cu jumatate din numarul total al rotilor unui metrou sau tramvai.

In figura 1.8.c este prezentata o caracteristica viteza - cuplu a unei actionari ce functioneaza la putere constanta. Exemple de astfel de actionari se pot intalni in fabricile de celuloza si hartie sau de materiale plastice. Figura 1.8.d prezinta caracteristica viteza - cuplu pentru un excavator. Portiunile AB, A'B' ale caracteristicii depind de natura materialului de excavat, iar cele notate cu BC si respectiv B'C' reprezinta limitarile ce trebuiesc avute in vedere, pentru a preveni distrugerea mecanica a excavatorului, in cazul in care pe durata procesului de sapare este intalnita o roca dura.

Caracteristica mecanica pentru o macara este prezentata in figura 1.8.e. Aici se poate observa faptul ca valoarea cuplului de sarcina nu depinde de viteza, el fiind constant si depinzand numai de acceleratia gravitationala g. Doar la viteze mari de lucru componenta de frecari vascoase a cuplului isi face simtita prezenta.

4. Clasificarea cuplului de sarcina

Cuplurile de sarcina pot fi impartite in doua mari categorii:

cupluri de sarcina active;

cupluri de sarcina pasive.

Prima categorie se refera la acele sarcini care isi pot mentine semnul cand directia de rotire a motorului actionarii se schimba si care au capacitatea de a antrena motorul principal in anumite conditii de echilibru. Exemplu de sarcini din aceasta categorie sunt: cuplul datorat fortei gravitationale (cazul unei macarale sau a unei masini care trebuie sa urce un deal, iar apoi sa il coboare) sau cuplurile datorate compresiei, respectiv torsiunii.

Cuplurile de sarcina pasive se opun mereu cuplului dezvoltat de catre masina de lucru. Este si cazul cuplului datorat frecarilor.

5. Stabilitatea statica de functionare

Conform relatiei 1.9, viteza de regim stationar a unei actionari este atinsa atunci cand cuplul dezvoltat de motor este egal cu cel cerut de catre sarcina. Aceasta viteza, numita viteza de echilibru, este viteza corespunzatoare punctului de functionare in care actionarea va reveni, dupa aparitia unei mici perturbari externe (variatia tensiunii de alimentare, mici vibratii, etc.). Analiza stabilitatii actionarii intr-un punct de functionare se face pe baza conceptului de stabilitate statica de functionare, cu folosirea caracteristicilor viteza - cuplu stationare atat pentru masina, cat si pentru sarcina. Se presupune ca indepartarea fata de acest punct de echilibru se face de-a lungul caracteristicilor stationare. Daca notam cu indicele e variabilele la echilibru, atunci avem:

                                  (1.10)

                      (1.11)

In cazul aparitiei unei perturbatii, cuplul motorului, cel al sarcinii si respectiv viteza, vor fi perturbate de catre marimile notate aici cu: m, m_S si _m. Relatia 1.9 devine:

              (1.12)

iar din relatiile 1.10, 1.11 si 1.12 rezulta ecuatia diferentiala a unor mici pertubatii in jurul punctului static de functionare (a punctului de echilibru):

      (1.13)

Pentru variatii foarte mici, caracteristicile motorului si ale sarcinii pot fi considerate lineare si atunci putem scrie:

                 (1.14)

(1.15)

Valorile din paranteze reprezinta tangentele la caracteristicile viteza - cuplu, pentru punctul considerat. Inlocuind ultimile doua relatii in ecuatia 1.13 se obtine:

                     (1.16)

Daca pentru aceasta ecuatie diferentiala punem conditia initiala ca la t = 0, _m = 0, se obtine solutia:

                           (1.17)

Punctul de echilibru se defineste a fi static stabil, daca _m tinde catre zero cand timpul t tinde catre infinit in relatia 1.17. Acest lucru are loc atunci cand paranteza din relatia anterioara ia o valoare pozitiva:

                  (1.18)

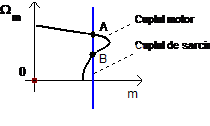
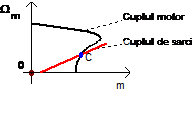
Rezulta ca la o crestere a valorii vitezei actionarii _m, variatia cuplului de sarcina trebuie sa fie mai mare decat cea a motorului, facilitand revenirea in punctul de functionare initial. Tinand cont de aceste consideratii, in figura 1.9 sunt exemplificate doua puncte de functionare stabile (A si C) si unul instabil (B).

a) b)

Fig. 1.9. Stabilitatea statica de functionare.