
|
|
|
MATERIALE DIELECTRICE SOLIDE
Scopul lucrarii
Scopul acestei lucrari este determinarea permitivitatii complexe relative a materialelor dielectrice solide uzuale si analiza comportarii acesteia in frecventa.
Dielectricii sunt materiale care se caracterizeaza prin stari de polarizatie cu functie de utilizare. Prin stare de polarizatie electrica se intelege starea materiei caracterizata prin momentul electric al unitatii de volum diferit de zero. Starea de polarizatie poate fi temporara daca depinde de intensitatea locala a campului electric in care este situat dielectricul si poate fi de deplasare (electronica sau ionica) sau de orientare dipolara. Starea de polarizatie permanenta nu depinde de intensitatea locala a campului electric si poate fi spontana (piroelectrica) sau piezoelectrica.
Daca un material dielectric cu permitivitatea complexa relativa e, se introduce intre armaturile unui condensator avand in vid capacitatea Co in aproximatia ca liniile de camp se inchid in intregime prin material (efectele de margine sunt neglijabile), admitanta la bornele condensatorului astfel format are expresia:
![]() (2)
(2)
Deci, condensatorul cu materialul dielectric intre
armaturi este echivalent cu un condensator fara pierderi, Ce
= e Co,
avand si o rezistenta de pierderi in paralel cu condensatorul,
de valoare 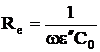
Schema echivalenta si diagrama fazoriala sunt date in Figura 1.
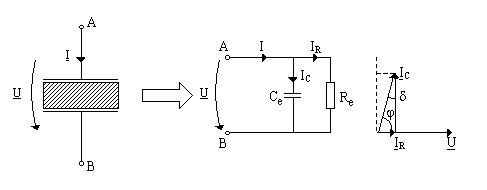
Figura 1. Schema echivalenta si diagrama fazoriala pentru
un condensator cu dielectric intre armaturi
Din schema echivalenta se observa ca partea reala a permitivitatii complexe relative caracterizeaza dielectricul din punct de vedere al proprietatilor sale de a se polariza (indiferent de mecanismul de polarizare) si are ca efect cresterea de e ori a capacitatii condensatorului la aceleasi dimensiuni geometrice, capacitatea condensatorului obtinut fiind :
Ce = e Co (3)
Partea imaginara a permitivitatii complexe relative e , caracterizeaza dielectricul din punct de vedere al pierderilor de energie in material, pierderi modelate prin rezistenta
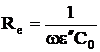 (4)
(4)
In diagrama fazoriala din Figura 1, unghiul j este unghiul dintre tensiunea U aplicata condensatorului si curentul I care il strabate. Complementarul unghiului de fazaj j se numeste unghi de pierderi si se noteaza cu d
Se defineste tangenta unghiului de pierderi a materialului dielectric, ca fiind raportul:
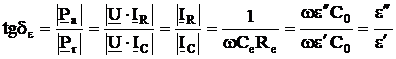 (5)
(5)
unde: Pa: puterea activa la bornele condensatorului
Pr: puterea reactiva la bornele condensatorului
Inversul tangentei unghiului de pierderi se numeste factor de calitate al materialului dielectric si se noteaza cu
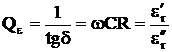 (6)
(6)
Observatii: Pe parcursul efectuarii calculelor si intocmirii tabelelor s-a observat o diferenta mica intre valorile obtinute prin masurare si cele obtinute prin calcul matematic , diferenta ce se datoreaza erorilor de masurare dar si a uzurii placutelor care au ajutat la efectuarea experimentului .
F [Mhz]
100
200
300
400
500
600
700
800
900
1000
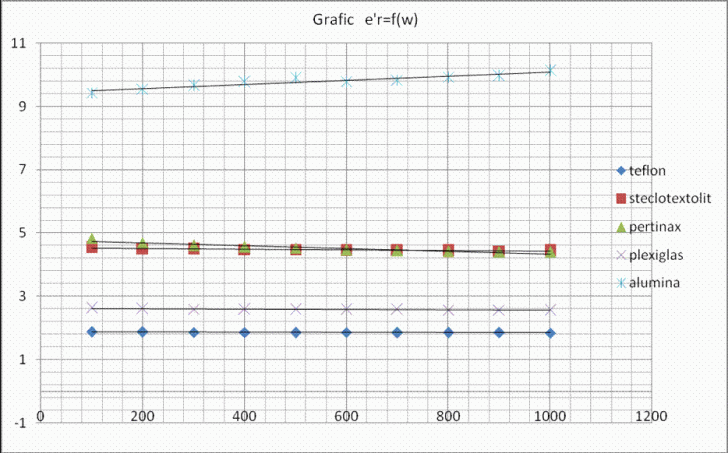
teflon
ε'r
1.87598
1.87063
1.86342
1.86042
1.85827
1.85912
1.85604
1.85192
1.85003
1.8438
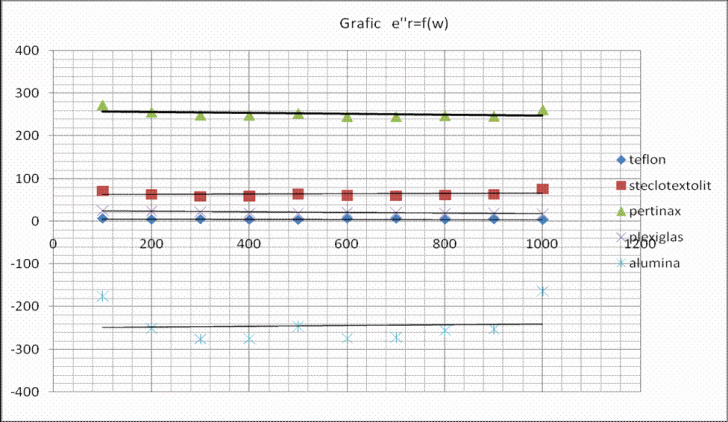
ε''r
6.82182
4.43271
5.12398
3.86187
3.71733
6.65669
6.22773
4.2135
4.87417
3.36598
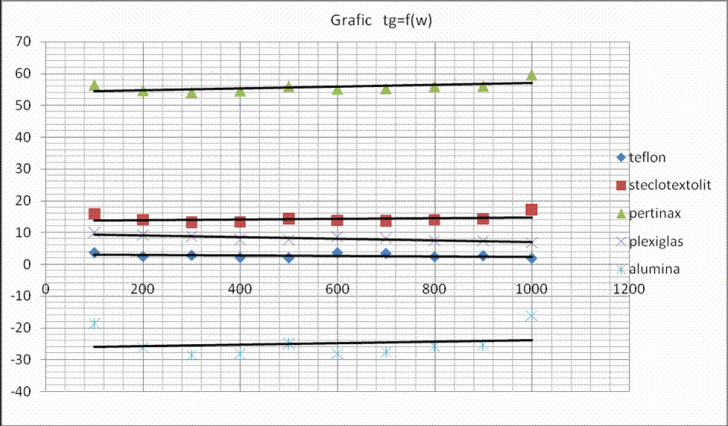
tgδ
3.63615
2.36957
2.74975
2.07573
2.00043
3.58054
3.35537
2.2752
2.63465
1.82557
Qε
0.274997
0.422006
0.363667
0.481741
0.499894
0.279286
0.298028
0.439521
0.379558
0.547775
steclotextolit
ε'r
4.54536
4.50299
4.48969
4.47942
4.47602
4.45101
4.44426
4.44349
4.43624
4.43907
ε''r
71.9604
63.0569
58.7333
59.4799
63.964
61.0062
60.3925
62.005
63.0138
76.2035
tgδ
15.8316
14.0032
13.0817
13.2785
14.2904
13.7061
13.5889
13.9541
14.2043
17.1665
Qε
0.063165
0.071412
0.076442
0.07531
0.069977
0.07296
0.07359
0.071663
0.070401
0.058253
pertinax
ε'r
4.83771
4.6889
4.61437
4.56142
4.52512
4.47308
4.44429
4.42353
4.40086
4.39121
ε''r
273
256.251
249.311
249.084
253.444
246.064
245.699
247.726
246.761
261.942
tgδ
56.4314
54.6589
54.0293
54.6066
56.0082
55.101
55.2842
56.0019
56.0712
59.6515
Qε
0.017721
0.018298
0.018508
0.018313
0.017855
0.018179
0.018088
0.017857
0.017835
0.016764
plexiglas
ε'r
2.62864
2.60922
2.59656
2.58796
2.58193
2.58409
2.57888
2.57192
2.57018
2.56249
ε''r
26.2293
24.0985
22.628
20.1856
19.6888
22.103
20.9748
19.2126
19.1245
17.3551
tgδ
9.97826
9.23593
8.71461
7.79981
7.62562
8.55351
8.13327
7.47016
7.44092
6.77275
Qε
0.100218
0.108273
0.11475
0.128208
0.131137
0.116911
0.122951
0.133866
0.134392
0.147651
alumina
ε'r
9.42797
9.5454
9.65507
9.77274
9.88565
9.78088
9.83681
9.92919
9.96693
10.1298
ε''r
-174.891
-250.95
-275.874
-275.411
-246.566
-274.685
-272.379
-256.377
-253.145
-163.318
tgδ
-18.5499
-26.2894
-28.5727
-28.1816
-24.9418
-28.084
-27.6898
-25.8206
-25.3985
-16.1225
Qε
-0.05391
-0.03804
-0.035
-0.03548
-0.04009
-0.03561
-0.03611
-0.03873
-0.03937
-0.06203
F [Mhz]ε'r1 ,ε'r2 ,ε're
100
500
800
Pertinax
ε'r1
4.83771
4.52512
4.42353
Steclotextolit
ε'r2
4.54536
4.47602
4.44349
ε're masurat
4.80695
4.56057
4.48301
ε're calculat
4.683239
4.499807
4.433743
ε're mas-ε're calc
0.123711
0.060763
0.049267
Intrebari si Raspunsuri
1. Cum comentati comportarea materialelor masurate la diferite frecvente?
Valorile permitivitatii relative reale sunt comparabile cu cele reale, da putin mai mici in timp ce pierderile sunt mai mari. Aceasta este o subliniere a realitatii. Deoarece in partea de teorie o serie de influente externe si interne (datorate structurii imperfecte sau) au fost neglijate, este normal sa apara diferente. In plus o mare parte a acestor diferente se datoreaza aparaturii de laborator folosita (care are limitarile ei).
Este evident din masuratorile efectuate ca folosireea acestor materiale este recomandata la frecvente mici deoarece la frecvente mari pierderile sunt mult mai mari (la unele materiale chiar duble - teflon).
2. Sa se deduca formula de calcul a tangentei unghiului de pierderi echivalente a doua condensatoare legate in paralel si in serie cand se cunoaste capacitatea si tangenta unghiului de pierderi pentru fiecare condensator.
Din formula Taylor rezulta :
Conexiunea in serie : Conexiunea in paralel :
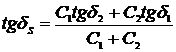
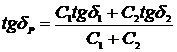
3. Sa se calculeze permitivitatea complexa echivalenta a unui dielectric format din doua straturi de materiale diferite, cand se cunoaste permitivitatea complexa a fiecaruia (vezi Figura 10).
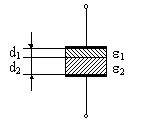
Figura 10
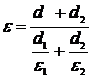
4. Sa se calculeze rezistenta echivalenta de pierderi in paralel, pentru fiecare condensator auxiliar folosit la doua din frecventele pentru care s-au facut masuratorile.
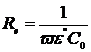
Condensatorul
![]() [pF]
[pF]
![]() [MHz]
[MHz]
![]()
![]() [kΩ]
[kΩ]
1
7,8
0,3
0,1443
0,47
1
7,8
2
0,1265
0,08
2
33,33
0,5
0,0029
3,29
2
33,33
1
0,0027
1,77
3
5
0,3
0,0059
17,99
3
5
5
0,0059
1,08