|
|
|
FACULTATEA DE ELECRONICA, TELECOMUNICATII SI TEHNOLOGIA INFORMATIEI
Materiale pentru Electronica
LABORATOR
MATERIALE FEROELECTRICE
I. Scopul Lucrarii
Scopul acestei lucrari este determinarea dependentei de frecventa si temperatura a permitivitatii complexe relative si studiul efectului piezoelectric pentru materiale ceramice feroelectrice.
II. Notiuni Teoretice
Materialele cu polarizare spontana sunt materiale care se caracterizeaza prin existenta unui moment electric nenul al unitatii de volum in absenta unui camp electric exterior. Celula elementara a unui asemenea material prezinta moment dipolar spontan printr-unul din urmatoarele mecanisme:
polarizarea de deplasare a electronilor atomici;
polarizarea de deplasare a ionilor celulei elementare.
Pentru ca intr-un material sa existe polarizatie spontana este necesar ca simetria structurala a materialului sa constituie, conform principiului lui Neumann, un subgrup al clasei de simetrie limita m; din cele 32 de clase de simetrie cristalina existente in natura, numai 10 indeplinesc aceasta conditie si anume: 1, 2, 3, 4, 6, m, mm, 3m, 4mm, 6mm.
Starea feroelectrica reprezinta o stare de ordine a materiei, rezultata spontan din tendinta catre stabilitate care corespunde unui minim al energiei libere totale a materialului.
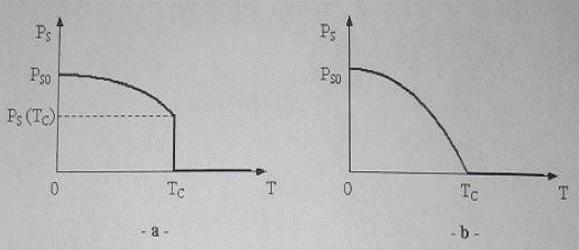
Dupa modul in care are loc tranzitia de faza la temperatura Curie TC materialele feroelectrice se impart in doua categorii:
materiale cu tranzitie de faza de ordinul I caracterizate prin anularea cu salt a polarizatiei spontane la TC ;
materiale cu tranzitie de faza de ordinul II caracterizate prin scaderea monotona si continua a polarizatiei spontane la TC .
Principalele caracteristici ale materialelor feroelectrice sunt dependenta de tip histerezis a inductiei electrice de intensitatea campului electric aplicat si dependenta permitivitatii complexe relative de intensitatea campului electric, de frecventa si temperatura.
Prin lucrarea de fata ne dorim determinarea parametrilor de material caracteristici ceramicelor piezoelectrice de tip PZT care contin titanati si zirconati de plumb in diferite concentratii si se obtin prin sinterizare. Din punct de vedere al proprietatilor electroelastice, ceramicele de tip PZT prezinta o simetrie de tip m, determinata de existenta unei axe polare pe directia x3, fiind caracterizate de urmatoarele configuratii ale matricilor de material:
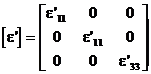
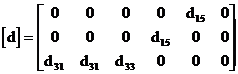
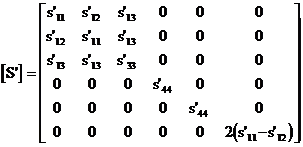
III. Mod de lucru
1.Determinarea dependentei de frecventa a permitivitatii complexe relative
Se foloseste o placheta de PZT cu grosimea b=3mm care se introduce intr-un dispozitiv de proba cu aria armaturilor A=80mm2.
Se determina permitivitatea relativa reala ![]() , permitivitatea relativa imaginara
, permitivitatea relativa imaginara ![]() si tangenta
unghiului de pierderi
si tangenta
unghiului de pierderi ![]() cu relatiile :
cu relatiile :
![]()
![]()
![]() unde
unde
![]() este permitivitatea
elastica absoluta a vidului :
este permitivitatea
elastica absoluta a vidului : ![]() =8,856 10-12
F/m
=8,856 10-12
F/m
F[MHz]
0,3
0,5
1
2
5
10
20
40
C[pF]
142.47
136.35
137.86
141.76
145.03
153.16
196.66
33.63[nH]
R[Ω]
1510
470.9
69.8
10.77
2.72
1.42
0.975
1.5
ε'
603.2774
577.3628
583.7567751
600.2710027
614.1175474
648.5433604
832.7405149
ε''
280425
899218
6066500.493
39316781.28
155677108.2
298198404.5
434299214.8
tgδ
464.8359
1557.457
10392.17145
65498.38507
253497.248
459797.1743
521530.0649
![]()
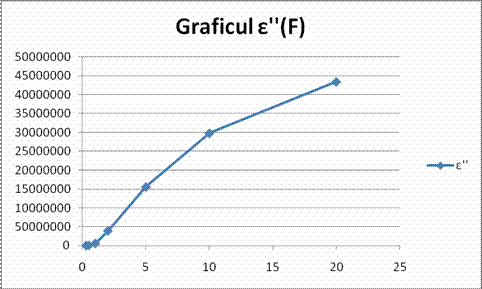
![]()
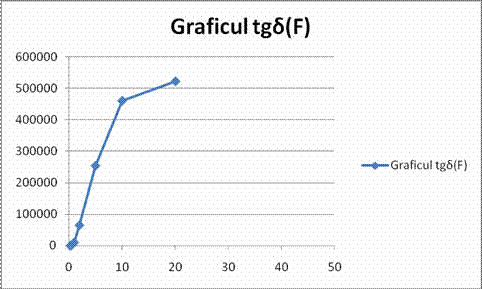
Cole-Cole e e
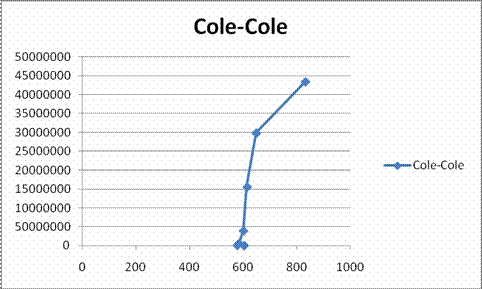
2. Determinarea dependentei de temperatura a permitivitatii complexe relative
Se determina variatia lui ![]() si
si ![]() in intervalul
de temperaturi 20o-300oC. Proba de material feroelectric
are grosimea b=3 mm si aria armaturilor A=80mm2. Se regleaza
autotransformatorul pe pozitia de aproximativ 110V/50Hz astfel incat cuptorul
sa-si modifice lent temperatura si se fac citiri din 5oC in 5oC
pana la temperatura de 250oC (pana la o temperatura cu aproximativ
50oC mai mare decat TC). La fiecare valoare a
temperaturii se masoara
in intervalul
de temperaturi 20o-300oC. Proba de material feroelectric
are grosimea b=3 mm si aria armaturilor A=80mm2. Se regleaza
autotransformatorul pe pozitia de aproximativ 110V/50Hz astfel incat cuptorul
sa-si modifice lent temperatura si se fac citiri din 5oC in 5oC
pana la temperatura de 250oC (pana la o temperatura cu aproximativ
50oC mai mare decat TC). La fiecare valoare a
temperaturii se masoara ![]() si
si ![]() . Unde
. Unde ![]() =
=![]() -1.
-1.
Se calculeza ![]() ,
, ![]() ,
, ![]() cu ajutorul
relatiilor de mai jos si stiind ca factorul de calitate al probei este
cu ajutorul
relatiilor de mai jos si stiind ca factorul de calitate al probei este ![]() iar
iar![]() este frecventa
unghiulara de lucru a puntii de masura. Valorile calculate se gasesc in Tabelul
2.
este frecventa
unghiulara de lucru a puntii de masura. Valorile calculate se gasesc in Tabelul
2.
![]()
Tabelul 2 :
T (° C)
C (nF)
R (kΩ)
ε΄
ε΄΄
tgδε
Q
21
0.0019
183
423.4417
2313.889259
0.000546
1830
80
1.1
368.5
465.7859
1149.095616
0.000247
4053.5
85
1.22
324.15
516.5989
1306.314158
0.000253
3954.63
90
1.37
291.9
580.1152
1450.639721
0.00025
3999.03
95
1.53
256.6
647.8659
1650.201615
0.000255
3925.98
100
1.76
225.5
745.2575
1877.790397
0.000252
3968.8
105
1.95
212
825.7114
1997.366672
0.000242
4134
110
2.14
191
906.1653
2216.972432
0.000245
4087.4
115
2.37
170
1003.557
2490.833732
0.000248
4029
120
2.57
154.9
1088.245
2733.6458
0.000251
3980.93
125
2.8
140.8
1185.637
3007.398682
0.000254
3942.4
130
3
132
1270.325
3207.891927
0.000253
3960
135
3.08
126.2
1304.201
3355.322777
0.000257
3886.96
140
3.1
123.5
1312.669
3428.678011
0.000261
3828.5
145
3.07
122
1299.966
3470.833889
0.000267
3745.4
150
2.99
120
1266.091
3528.68112
0.000279
3588
155
2.88
118.2
1219.512
3582.417381
0.000294
3404.16
T (° C)
C (nF)
R (kΩ)
ε΄
ε΄΄
tgδε
Q
160
2.75
115.5
1164.465
3666.162203
0.000315
3176.25
165
2.58
110.5
1092.48
3832.051895
0.000351
2850.9
170
2.46
106.5
1041.667
3975.978727
0.000382
2619.9
175
2.33
101.8
986.6192
4159.545525
0.000422
2371.94
180
2.19
94.2
927.3374
4495.135185
0.000485
2062.98
185
2.08
88.2
880.7588
4800.926694
0.000545
1834.56
190
1.97
81.57
834.1802
5191.145451
0.000622
1606.929
195
1.87
74.6
791.836
5676.16266
0.000717
1395.02
200
1.77
66
749.4919
6415.783855
0.000856
1168.2
205
1.68
58.46
711.3821
7243.272912
0.001018
982.128
210
1.61
52.2
681.7412
8111.910621
0.00119
840.42
215
1.54
46.66
652.1003
9075.047887
0.001392
718.564
220
1.48
40.18
626.6938
10538.61957
0.001682
594.664
225
1.46
33.8
618.2249
12527.86197
0.002026
493.48
230
1.39
30.13
588.584
14053.82457
0.002388
418.807
235
1.35
26.02
571.6463
16273.70232
0.002847
351.27
240
1.32
23.45
558.9431
18057.21682
0.003231
309.54
245
1.29
21.17
546.2398
20001.97139
0.003662
273.093
250
1.27
19.23
537.771
22019.85098
0.004095
244.221
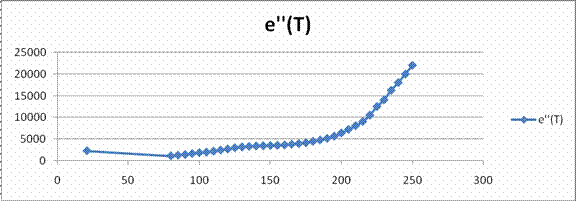
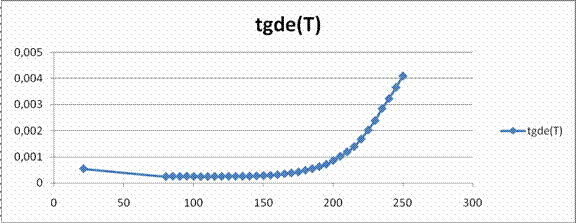
In
continuare trasam diagramele ![]() ,
, ![]() ,
, ![]()
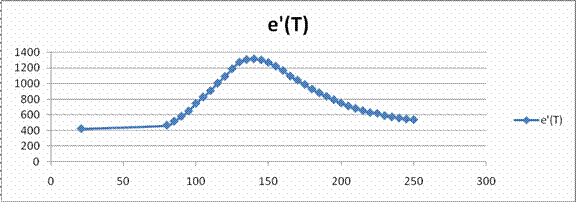
![]()
![]()
Pentru calcularea lui![]() la
la ![]() si la
si la ![]() se folosesc
formulele:
se folosesc
formulele:
![]() pentru
pentru ![]() deci
deci
![]()
![]()
![]() pentru
pentru ![]() deci
deci
![]()
![]()
3.Determinarea parametrilor de material elastici si piezoelectrici
Metoda de determinare a proprietatilor materialelor piezoelectrice este o metoda dinamica de rezonanta. Ea se bazeaza pe faptul ca prin aplicarea unui camp electric sinusoidal de frecventa f punctele materiale ale unei probe piezoelectrice vor oscila elastic fortat cu aceeasi frecventa f.
![]()
![]()
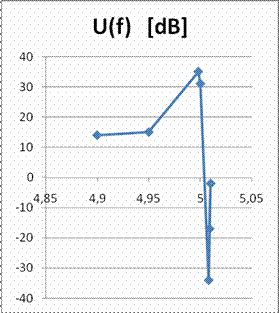
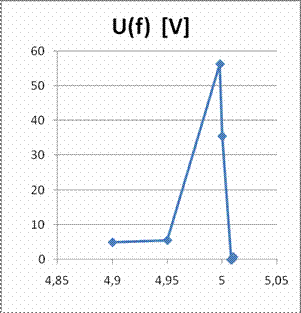
Rezonator piezoelectric cu cuart 4,8-5,2 MHz
![]()
4,9
4,95
4,998
5
5,008
5,01
5,009
![]()
14
15
35
31
-34
-2
-17
![]()
5,01
5,62
56,2
35,4
0,01
0,79
0,14
III .INTREBARI SI RASPUNSURI
1. Prezentati elementele de simetrie caracterisitice cristalelor dielectrice din clasele de simetrie mm, 3m, si 6mm. Caror sisteme cristalografice le apartin aceste cristale?
Aceste clase de simetrie: mm, 3m si 6mm, fac parte din cele 10 din 32 clase care indeplinesc conditia ca in material sa existe polarizatie spontana.
Aceste cristale apartin sistemelor cristalografice monocristale. Acestea sunt anizotrope, fortele exterioare sunt simetrice, volumul dintr-un exantion de monocristal este mai mic decat cel ocupat de acelas numar de particule daca materialul este amorf.
2. Sa se deterimine configuratie tensorului de permitivitate pentru cristalul de niobat de litiu care face parte din clasa de simetrie 3m.
Facand parte din clasa de simetrie 3m, rezulta ca tensorul de permitivitate va fi de ordinal 3.
![]()
![]() U
U![]()
![]() (27 de componenete)
(27 de componenete)
![]()
![]() U
U![]() = a
= a![]() a
a![]() a
a![]() U
U![]() = U
= U![]() ( unde am notat
cu
( unde am notat
cu ![]() tensorul permitivitatii);
tensorul permitivitatii);
Iar configuratia va arata astfel:
Matricea: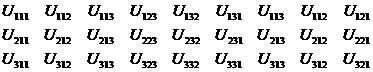
3. Sa se prezinte dependenta de tip histerezis a inductiei electrice de intensitatea campului electric caracteristica unui material ferroelectric.
Principalele caracteristice ale materialelor feroelectrice sunt dependenta de histerezis a inductiei electrice de intensitatea campului electric aplicat si dependenta permitivitatii complexe relative de intensitatea campului electric de frecventa si temperature.
In domeniul liniar de semnal mic, in regim armonic, este valabil urmatorul sisitem de ecuatii:
![]() =
= ![]()
![]()
![]()
E- reprezinta in complex semnificatia vectorului camp electric
T- reprezinta in complex tensorul matricii
D- reprezinta in complex inducita electrica
S- reprezinta in complex deformarea elastica
4. Prin ce proprietati fizice difera materialele feroelectrice cu tranzitie de faza de ordinal I de materialele feroelectrice cu tranzitia de faza de ordinal II?
Materialele cu tranzitie de faza de ordinal I se caracterizeaza prin anularea cu salt al polarizatiei spontane la temperature Curie, pe cand la materialele cu tranzitie de ordinal II, polarizatia spontana scade monoton si continuu la temperature Curie (Tc)