|
|
|
ELEMENTE DE MECANICA ACTIONARII - MASINI ELECTRICE
S1. Legile miscarii corpului solid
In paragraful 1.3.1 a fost prezentata ecuatia de miscare, pornind de la legea fundametala a dinamicii. Daca formula 1.1.b. este pentru o miscare de rotatie, in cazul unei miscari rectilinii, ecuatia este (relatia 1.1.a):
(1.19)
Aceste ecuatii sunt utile in studierea proceselor tranzitorii. Cuplul care actioneaza asupra unui corp este definit astfel:
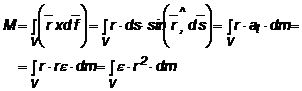(1.20)
Conform acestei relatii, se defineste momentul de inertie axial al unui corp fata de o axa de rotatie ce trece prin centrul de greutate al sau si care in cazul nostru, este arborele masinii:
(1.21)
unde : dm este masa elementului de volum situata la distanta r de ax.
Daca consideram masa concentrata intr-un punct la distanta r de ax, atunci pentru momentul de inertie se obtine urmatoarea relatie:
(1.22)
cu J in kgm2. Prin combinarea relatiilor 1.9, 1.22 si introducerea vitezei de rotatie in rot/min, rezulta:
(1.23)
Aplicatie Sa se gaseasca relatia momentului de inertie pentru un cilindru plin si unul gol.
1. Cilindru plin Daca raza cilindrului este R, atunci putem scrie relatiile:
Aria cilindrului 
(1.24)
Tabelul 1.2.
Volumul cilindrului 
(1.25)
Masa
cilindrului 
(1.26)
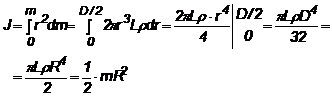(1.27)
Atunci cand vorbim despre un punct material cu acelasi moment de inertie cu cel al corpului, putem defini raza de giratie, care este:
(1.28)
si ecuatia
1.27 devine: 
(1.29)
cu 
moment de giratie.
|
|
|
|
2. Cilindru gol
Fig. 1.12. Determinarea momentului de inertie
al unui cilindru gol.
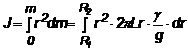(1.30)
(1.31)
Dar:
(1.32)
cu 
, greutatea specifica
a corpului. Rezulta aceeasi formula pentru momentul de inertie:
(1.33)
cu raza de giratie definita:
(1.34)
Observatie: Daca acest cilindru ar fi plin, atunci R1 = 0 si se obtine acelasi rezultat ca si la punctul anterior.
S2. Raportarea cuplurilor si fortelor la acelasi arbore
Ecuatia 1.10 reprezinta ecuatia de echilibru a cuplurilor raportate la acelasi arbore. Acest lucru este necesar, datorita faptului ca de cele mai multe ori, diferitele parti componente aflate in miscare ale sistemului de actionare electrica, au viteze diferite. Pentru aceasta, se realizeaza o raportare a cuplurilor, fortelor, momentelor de inertie si a maselor, la acelasi arbore (arborele masinii principale a actionarii).
Pentru a deduce relatiile de raportare, vom considera schema din figura 1.14, un sistem de actionare cu transmisia realizata cu roti dintate. Problema se trateaza asemanator chiar daca este vorba de un alt tip de transmisie (hidraulica, cu curele, pneumatica, etc.).
Raportul de transmisie, i, reprezinta de cate ori este mai mare viteza unghiulara a arborelui motorului decat cea a arborelui condus al masinii de lucru (figura 1.13).
(1.35)
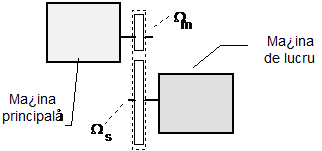
Fig. 1.13. Raportul de transmisie.
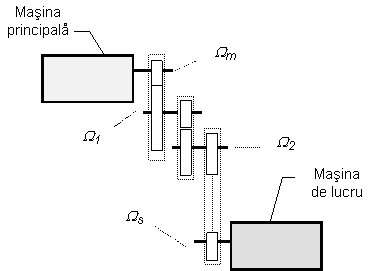
Fig. 1.14. Actionare electrica cu transmisie cu roti dintate.
Prin egalarea succesiva a puterilor la arbori (Legea Conservarii Puterii) si considerand transmisia ideala (pierderi neglijabile in transmisie), se obtine:
(1.36)
rezultand cuplul de sarcina raportat la arborele motorului:
(1.37)
iar daca consideram o transmisie cu pierderi, atunci se obtine:
(1.38)
In cazul transmisiilor elastice, apare o diferenta intre viteza reala a masinii de lucru si cea ideala. Acelasi fenomen apare si in cazul transmisiilor cu curele, datorita efectului de patinare a curelei. De aceea este necesara introducerea notiunii de alunecare, definita cu ajutorul relatiei urmatoare:
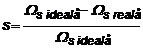(1.39)
si care va modifica raportul de transmisie, astfel:
(1.40)
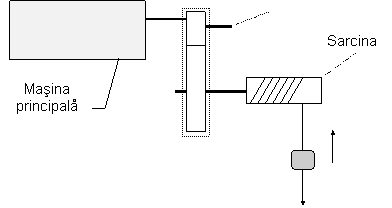
Unele sisteme de actionare realizeaza simultan cu transmisia de putere de la masina principala la cea de lucru si o transformare a miscarii de rotatie in miscare rectilinie. Este cazul podurilor rulante, a macaralelor, etc.
Relatia de raportare a cuplului cerut de catre sarcina, in aceste conditii, este:
(1.41)
M, m
m vS
FS
Fig. 1.15. Schema actionarii unui mecanism de ridicare.
S3. Raportarea momentelor de inertie si masei la acelasi arbore
Pentru a deduce relatia de raportare a momentelor de inertie la un singur arbore, facem apel la Legea Conservarii Energiei Cinetice. Se obtine astfel un moment de inertie echivalent:
(1.42)
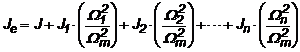(1.43)
Daca exista instalatii in care anumite componente executa o miscare de translatie, atunci se pune problema raportarii masei la arborele masinii principale a actionarii:
(1.44)
se obtine:
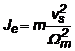(1.45)
iar daca consideram un cuplaj in trepte, o sarcina potentiala si randamentul transmisiei, atunci relatia globala a momentului de inertie total echivalent, raportat la arborele masinii este:
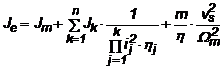(1.46)
unde : Jm este momentul de inertie al motorului;
vS viteza sarcinii;
j randamentul unui etaj al transmisiei.
