Costurile de productie in perioada scurta

COSTURILE DE PRODUCTIE IN PERIOADA SCURTA

Costul de productie al unei firme difera, sub aspectul structurii, in raport cu perioada de analiza. In perioada scurta firma actioneaza 'sub constrangere' intrucat nu poate modifica cel putin un factor de productie care ramane fix.

1. Tipologia costurilor

Atunci cand o firma produce o cantitate de bunuri, se pun trei intrebari: a) cat costa producerea intregii cantitati, q, de bunuri; b) cat costa fiecare obiect atunci cand se produce cantitatea q?; c) care este cresterea costului total atunci cand cantitatea totala de bunuri produse sporeste cu o unitate?

Raspunsul la aceste intrebari evidentiaza existenta mai multor tipuri de costuri.

A) COSTUL TOTAL (C_T) este definit ca ansamblul cheltuielilor de factori de productie corespunzator unui volum dat de productie. Ca oricare fenomen economic relevant, costurile totale nu au o evolutie uniforma in timp, mai ales din punct de vedere al marimii lor. Modificarea, ca cerinta a dinamicii, este o coordonata in domeniul costurilor inca de la introducerea in fabricatie a bunurilor.

Variabilele economice care influenteaza asupra evolutiei costurilor sunt multiple. Dintre acestea, cercetarea stiintifica a reliefat pe larg efectele pe care le are evolutia productiei asupra dinamicii si structurii costurilor.

Actionand ca o variabila independenta, productia genereaza o relatie functionala cunoscuta sub numele de functia costurilor. Pentru a obtine o expresie simpla a functiei costurilor trebuiesc admise mai multe ipoteze: o intreprindere produce un singur bun cu ajutorul anumitor factori de productie din care unii sunt folositi in cantitati fixe, indiferent de volumul productiei, iar cheltuielile legate de acesta sunt cunoscute si constante, alti factori sunt variabili si pot fi obtinuti la pretul pietei. Se presupune, de asemenea, ca totalul capitalului real si cunostintele tehnice raman neschimbate iar intreprinderea isi organizeaza activitatea incat sa obtina productia la costuri minime. In acest caz, costul total depinde de cantitatea productiei si numai de productie, adica: C_T=F(q).

In conditiile in care un factor de productie este fix, pe termen scurt, costul acestui factor nu se modifica odata cu cantitatea produsa. Functia costurilor totale este urmatoarea:

C_Ts = C_F + C_V

sau

C_Ts = C_F + F(q),

unde C_Ts reprezinta costul total pe termen scurt, C_F reprezinta costul fix, adica o suma constanta si egala cu costul factorului fix, oricare ar fi durata perioadei de utilizare, iar C_V, respectiv F(q), reprezinta functia costului variabil, adica acele costuri care se modifica in acelasi timp cu cantitatea productiei. Componenta fixa a costului total poate fi reprezentata de capital, un numar de masini si instalatii care au fost achizitionate de firma pe baza unui imprumut pentru care trebuie sa plateasca o dobanda (i):

C_F=iK.

Firma trebuie sa suporte aceasta cheltuiala chiar daca productia se reduce sau, dimpotriva, sporeste. Daca munca este singurul factor variabil, costul variabil este egal cu costul muncii. Cu cat firma foloseste mai multa munca, cu atat sporeste productia si costul variabil.

Functia costurilor totale este reprezentata prin curba costurilor totale ce descrie variatia costurilor cand productia creste. Forma functiei si a curbei costurilor depinde de diversi factori care influenteaza costul (tehnica de productie, munca, costurile de aprovizionare etc.). In fig. 5.1, costul total, costul fix si costul variabil sunt inscrise pe ordonata iar productia pe abscisa. Costul fix, C_F, este reprezentat de o dreapta orizontala pentru a exprima faptul ca nu se modifica in raport cu cantitatea produsa. Costul variabil, C_V sporeste la inceput cu o rata descrescatoare, iar apoi sporeste cu o rata crescatoare. Costul total C_T se obtine prin insumarea pe verticala a costului fix si a costului variabil.

Curba costurilor totale taie axa verticala (ordonata) intr-un punct situat deasupra originii (pozitia acestuia indica marimea costului fix), creste continuu de la stanga la dreapta si are o forma de S.

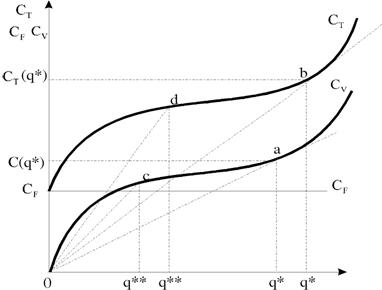
Fig. 5.1. Curbele costurilor pe termen scurt.

Cele mai frecvente tipuri de functii de cost total pot fi considerate urmatoarele:

C_T = aq + b (1)

C_T = aq² + bq + c (2)

C_T = aq + b + c (3)

C_T = aq³ - bq² + cq + d (4)

.                     (5)

Parametrii a,b,c,d sunt pozitivi. In cazul (2) curba este o parabola cu axa orientata vertical in sus si cu varful in stanga originii, in punctul q=-b/2a. Deoarece curba este limitata la primul cvadrat, ea consta dintr-un arc de parabola care creste continuu de la stanga la dreapta, asa cum poate fi reprezentata functia:

.

Parametrii functiei costurilor ne permit sa sesizam modificari de costuri. O curba a costurilor de forma (2) este fixa, daca a, b, c au valori date. Daca un parametru se schimba, intreaga curba a costurilor isi schimba pozitia. O modificare a lui "c" reprezinta o crestere a cheltuielilor constante si curba costurilor totale se deplaseaza in sus fara sa-si modifice forma. In schimb, variatia lui a si b corespund unor modificari de cheltuieli variabile si curba costurilor totale se modifica atat ca forma cat si ca pozitie.

In functie de dependenta fata de marimea si evolutia volumului fizic al productiei, pe termen scurt costurile totale se impart in costuri totale fixe si costuri totale variabile.

a) Costuri totale fixe (C_F) reprezinta, in perioada scurta, cheltuieli generale pe care trebuie sa le faca producatorul fata de o anumita capacitate de productie si care nu variaza daca se schimba volumul productiei. Daca se produce mai mult, mai putin sau nu se produce, aceste cheltuieli raman constante.

De regula, in aceasta categorie se includ urmatoarele: amortizarea capitalului fix, chirii, salariile personalului administrativ si de conducere, cheltuieli de intretinere, dobanzi etc. Curba costurilor fixe este o dreapta paralela la axa productiei. Costurile fixe reprezinta costuri actuale (paza, chirie, intretinere, asigurari, curatenie cote de participare, unele taxe si obligatii fiscale, unele cheltuieli salariale)si costuri trecute (rambursarea imprumuturilor si 'serviciul datoriei', amortizarea echipamentelor achizitionate in perioadele anterioare).

De regula, cheltuielile generale, de regie, care formeaza partea principala a continutului costurilor fixe, se structureaza in urmatoarele categorii:

- cheltuieli generale de productie, ce cuprind cheltuielile ocazionale de functionarea atelierelor, dar independente de cantitatea productiei (conducere, lumina, impozite fixe, paza contra incendiilor etc.);

- cheltuieli generale cu caracter comercial, care sunt determinate de procesul vanzarii marfurilor (publicitate, transport, ambalaj, comisionul intermediarilor etc.);

cheltuieli generale de administratie, respectiv cheltuielile directiei, de supraveghere, de functionare a serviciilor etc.

b) Costurile totale variabile (C_V) sunt acele elemente de cheltuieli a caror marime totala se modifica pe masura schimbarii volumului total al productiei. In aceasta categorie se includ cheltuielile pentru materii prime si materiale de baza, materiale auxiliare, salarii, combustibil si energie

C_V=F(Q).

Fata de o anumita crestere sau descrestere a volumului fizic al productiei, unele cheltuieli cresc sau scad in aceeasi proportie (materii prime, salarii directe), altele intr-o proportie mai mare, iar o a treia catego­rie se modifica intr-o proportie mai mica. Lipsa de stricta proportionalitate se datoreaza unor ratiuni de natura tehnica sau financiara. Consumul de materii prime este proportional cu volumul productiei, dar alte costuri pot evolua neproportional. Din motive tehnice, consumul de carburant nu este proportional cu viteza de deplasare a unui autovehicul. Costurile financiare cresc substantial daca sunt folosite ore suplimentare (ore peste durata normala de lucru), care sunt platite cu un tarif superior.

Costul variabil este nul pentru nivelul zero al productiei si este o functie crescatoare in raport cu productia. Ritmul de crestere este fluctuat: in prima faza ritmul este descrescator(F <0), apoi trece printr-un minim (F''=0), ceea ce inseamna ca exista un punct de inflexiune I in care curba costului total variabil isi traverseaza propria tangenta, dupa care devine crescator (fig.5.2). Ca si curba costurilor totale, curba costurilor totale variabile are o forma de S si porneste din origine.

In cazul in care costul fix este strict constant, cresterile costului variabil si a costului total in cazul sporirii productiei sunt intotdeauna riguros identice.

Intrucat costul total este egal cu suma costurilor fixe si a costurilor variabile, modificarea costurilor totale constituie rezultatul exclusiv al schimbarilor produse in costurile variabile:

C_T=C_V+C_F=(C_T-C_F)+C_F,

ceea inseamna ca:

C_T-C_V=C_T-(C_T-C_F)=C_F,

care se mentine acelasi pe intregul domeniu de variatie al costurilor totale.

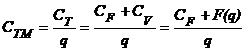
B. COSTUL TOTAL MEDIU (sau costul unitar) C_TM reprezinta costul total pe unitate de produs. El se determina prin raportul dintre costurile totale si volumul productiei, oricare ar fi el. Notand costul mediu cu C_TM obtinem:

C_TM=F(q)

unde,

Costul mediu variaza odata cu productia si avem o functie de cost mediu si o curba de cost mediu. Forma functiei si curbei costului mediu se obtine din cea a functiei si curbei costului total.

Daca pentru intreaga productie evolutia costului total se prezinta sub forma unei curbe crescatoare nonproportionale (curba S), costul mediu se inscrie pe o curba care are o forma oarecum inversa fata de precedenta.

Dependenta functionala a costurilor in raport cu productia evolueaza intr-o forma tipica, expresie a legii randamentelor nonproportionale, iar curba pe care o parcurg are conturul unei 'seceri fara varf', sau curba in forma de U. Ea porneste de la un nivel ridicat al costurilor medii corespunzatoare unui volum scazut de productie si coboara abrupt o data cu cresterea productiei. Costurile totale medii ating nivelul minim pentru q^*, corespunzator punctului de pe curba C_T unde o raza plecata din origine realizeaza un punct de tangenta (b) si care are o panta mai mica decat panta oricarei alte raze. Dincolo de acest punct, costul total mediu se mentine la un nivel relativ constant, cu toate ca productia sporeste. In cele din urma, cantitati suplimentare de productie se obtin cu costuri totale medii tot mai mari (fig.5.3).

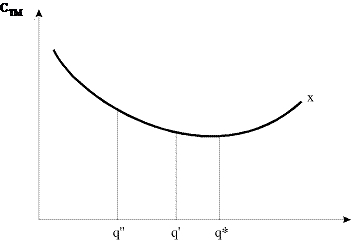
Fig.5.3 Curba costului total mediu

Evolutia curbei costurilor totale medii este determinata de efectul miscarii costurilor totale variabile care cresc odata cu cantitatea produ­selor, iar costurile fixe medii au o evolutie descendenta. Tendintele puse ale evolutiei costurilor fixe si variabile in structura costurilor totale constituie si cauza cea mai importanta, dar nu exclusiva a curbei costurilor totale medii. Atat timp cat cresterea costurilor variabile este compensata de scaderea celor fixe pe unitate de produs, costurile totale medii sunt descrescatoare. Atunci cand acest efect este anihilat, devine preponderenta cresterea costurilor fata de cea a productiei, iar panta costurilor totale medii incepe sa urce. Aceasta situatie se explica si prin influenta interdependentei dintre costuri, capacitatea de productie si cantitatea productiei.

Daca costurile totale sunt date de o functie de forma liniara, adica

C_T=aq+b

atunci:

.

In cazul in care costurile totale sunt exprimate de o parabola (2), adica,

C_T=aq²+bq+c

atunci,

,

ceea ce semnifica urmatorul aspect: la un nivel redus de productie, curba costului total mediu trebuie sa scada cand productia creste, iar la niveluri ridicate curba costului total mediu creste.

Costul total mediu este diferit: a) de la un produs la altul in depen­denta de specificul fiecaruia, de complexitatea mai mare sau mai redusa; b) la unul si acelasi produs, insa de la un producator la altul, in raport de randamentul economic, de conditiile concrete de productie etc.; c) in cadrul aceleiasi intreprinderi, de la o perioada la alta.

Deoarece costul total este format din costul fix si costul variabil, se distinge, pe langa costul total mediu, drept componente ale acestuia, costul fix mediu si costul variabil mediu.

a) Costul fix mediu (C_FM) reprezinta costul fix suportat de fiecare unitate de productie

.

Curba costului fix mediu este descrescanda, acelasi cost se repartizeaza asupra unei productii tot mai mari. Daca q , atunci C_FM 0 si invers. Ca urmare functia costului fix mediu are drept asimptote cele doua axe de coordonate.

Descresterea costului fix mediu este proportionala, in ipoteza randamentelor constante. In conditiile unor randamente nonproportionale, costurile fixe medii la inceput tind sa descreasca mai repede din cauza ca un volum total de cheltuieli se raporteaza pe un total mai mare de produse. Mai departe insa, proportia acestei micsorari se reduce, pana ce descresterea devine foarte mica.

b) Costul variabil mediu (C_VM) exprima costul variabil pe fiecare unitate de productie

.

Proportia variatiei medii a costurilor poate fi descrescatoare, constanta sau crescatoare. Cand costurile variabile cresc constant cu productia, atunci costurile medii sunt constante, iar daca costurile cresc intr-o proportie mai mica sau mai mare decat productia, atunci costurile variabile medii sunt descrescatoare sau crescatoare.

Daca salariul este singurul cost variabil si costul fix este egal cu zero, atunci costul total este produsul dintre rata salariului nominal (W) si cantitatea de munca (L). In acest caz, costul variabil mediu este egal cu costul total mediu (C_VM=C_TM) si

.

Cum L/Q=1/(Q/L),care este inversul productivitatii muncii (PM=Q/L)avem ceea ce inseamna ca, pentru un salariu dat, costul variabil mediu si productivitatea muncii variaza in sens invers.

Situatia tipica pentru o productie cu o lunga continuitate in timp este reprezentata de reducerea la inceput a costurilor variabile medii ca urmare a economiilor realizate la diferite operatiuni tehnologice, atingerea dimen­siunii optime a structurii productiei, optimizarea folosirii echipamentelor etc. Treptat aceste costuri tind sa se plafoneze la nivelul de economii maxim posibil de realizat si apoi cresc. Motivul pentru care costul variabil mediu sporeste la cantitate mai mare de productie, este acela ca munca devine mai putin productiva pe masura ce firma angajeaza mai multi lucratori la o cantitate data de capital, considerat factor fix. In plus, costurile variabile medii incep sa creasca ori de cate ori producatorul este obligat de a opera cu loturi neeconomice.

Curba costurilor variabile prezinta unele caracteristici:

este o curba in forma de U. Pe masura ce nivelul productiei creste, costul variabil mediu scade si apoi creste;

distanta pe verticala intre curba costului variabil mediu si costul total mediu, este dependenta de marimea costurilor fixe.

C. COSTUL MARGINAL (C_mg). Analiza interdependentei intre evolutia costurilor si a productiei pune in lumina faptul ca sporul de productie se realizeaza cu cheltuieli diferentiale si nu cu cheltuieli uniforme pe unitate de produs. Pentru maximizarea productiei si minimizarea cheltuielilor nu se poate opera numai cu costurile medii, este necesara cunoasterea costurilor marginale. Costurile marginale exprima sporul de cost total (DC_T) necesar pentru obtinerea unei unitati suplimentare de productie (DQ)

,

iar pentru DQ=1 rezulta C_mg=DC_T

Pentru o crestere infinit de mica a productiei, costul marginal este derivata functiei costului total (CT'=F'(q)) si, bineinteles, derivata functiei de cost variabil.

Din C_T=C_F+C_V=C_F+F(q), intrucat DC_F=0, rezulta ca:

.

Costul marginal este independent de costul fix, intrucat acesta din urma este independent de volumul productiei. El masoara rata cresterii costurilor totale si aproximeaza costul unei mici unitati aditionale de productie, de la nivelul dat. Deoarece costul marginal variaza odata cu productia la care este masurat, exista o functie a costului marginal si o curba a acestuia.

Daca C_T=aq+b,

atunci

,

iar cand                          C_T=aq²+bq+c

este                                 ,

ceea ce inseamna ca o dreapta crescatoare cu panta egala cu 2a reprezinta curba costului marginal.

Costul marginal poate fi, uneori, extrem de mic. Pentru o calatorie cu trenul in care exista locuri neocupate, costul unui nou pasager este practic egal cu zero. Nu este necesar nici capital suplimentar (vagoane) si nici forta de munca suplimentara. Alteori insa, costul marginal poate fi destul de ridicat. Sa reluam exemplul precedent. In conditii normale un tren format din 12 vagoane satisface pe deplin necesitatile de transport pe o anumita ruta si capacitatea sa este folosita in proportie de 95%. Dar, in preajma unor sarbatori, cererea de bilete sporeste, ceea ce necesita punerea in circulatie a unui tren suplimentar ce este folosit in proportie de 40%. Locurile suplimentare au fost obtinute cu un cost marginal foarte ridicat.

2. Relatii intre costul total, costul mediu si costul marginal

Intre cele trei forme ale costului exista relatii de interdependenta. Daca costul total este o suma de cost fix si cost variabil, costul total mediu se determina ca raport intre costul total si productie, in timp ce costul marginal reprezinta suplimentul de cheltuiala solicitat de sporirea productiei cu o unitate.

In raport cu productia, costul total este reprezentat intotdeauna printr-o curba crescatoare in forma de S. Cresterea acesteia este insa divizata de doua parti, pana la punctul I numit punct de inflexiune, cresterea se diminueaza treptat si curba isi intoarce concavitatea in jos; dincolo de punctul I cresterea costului total se accelereaza iar curba isi intoarce concavitatea in sus. De aici rezulta ca pana la punctul I este intotdeauna avantajos sa se aloce cantitati sporite de factori variabili la factorul fix, pentru ca costul total al productiei creste din ce in ce mai putin. Dincolo de punctul I, situatia se inverseaza.

Curbele de cost total mediu sau cost marginal au o forma de U. Aceasta forma se aplica prin legea randamentelor descrescatoare care tinde intotdeauna si se impune in ultima instanta. La inceput influenta acestei legi poate fi contracarata de o puternica tendinta crescatoare a randamentelor ca efect al economiilor inerente productiei pe scara mai mare asociate la posibilitatea de a pune in practica o diviziune a muncii mai adancita. Or, daca randamentele cresc, costul marginal trebuie sa scada. Ulterior, insa, randamentele descresc si costurile cresc. Din punct de vedere logic, situatia se prezinta in felul urmator: in timpul unei perioade scurte consideram un factor de productie constant (un utilaj cu capacitate de productie invariabila). Se presupune ca putem face sa varieze cantitatea de productie obtinuta modificand volumul utilizat al unui factor de productie variabil, precum mana de lucru.

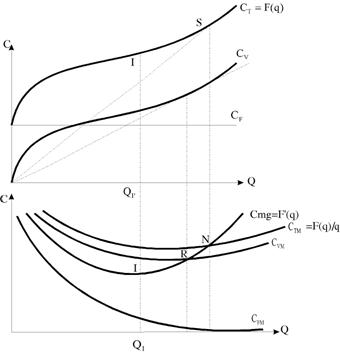
Fig 5.4. Costurile totale si costurile medii in perioada scurta.

Daca mana de lucru se angajeaza la acelasi nivel de salariu, singurul motiv pentru care s-ar ridica costurile corespunzatoare cresterii productiei ar fi scaderea productiei aditionale obtinuta prin intrari succesive de mana de lucru. In consecinta, daca modificarea factorului de productie variabil se concretizeaza in randamente descrescatoare ea se va concretiza, de asemenea, prin costuri marginale si costuri medii crescatoare (fig. 5.4).

Pozitiile relative ale curbelor de cost mediu si cost marginal se explica prin:

a)   nivelul minim N, al costului total mediu, coincide cu punctul S punct de tangenta al dreptei care porneste din origine, cu curba costului total. Inclinarea dreptei este exprimata de F(q)/q si dincolo de S, inclinarea incepe sa recreasca. Descresterea costurilor totale medii pana la punctul N in care ele ating minimul si apoi are loc o schimbare a degresiunii intr-o tendinta de crestere, se explica, pe de o parte, prin scaderea costurilor fixe pe unitate de produs ca si a celor variabile datorita unei mai bune combinari a factorilor de productie, iar pe de alta parte, prin cresterea progresiva a unor cheltuieli pentru un anumit volum de productie cum ar fi: utilizarea de ore suplimentare platite cu un tarif progresiv; depasirea gradului normal de folosire a utilajelor ce sporeste cheltuielile cu intretinerea si functionarea acestora etc.;

b)   nivelul minim R al costului variabil mediu se produce inaintea minimului costului total mediu si sub nivelul acestuia. Decalajul reprezinta influenta costurilor fixe, iar cauzele evolutiei sunt aceleasi ca in cazul C_TM.

c)   nivelul minim I al costului marginal corespunde punctului de inflexiune I, al curbei costului total C_T. Se observa ca pana la I, costul marginal, in functie de productie q, scade, apoi dincolo de I, sporeste.

d)   curba costului marginal C_mg intersecteaza curba costului variabil mediu C_VM si curba costului mediu C_TM in punctele R si N in care ele sunt minime.

Atat timp cat costul marginal este inferior costului total mediu (costul variabil mediu), costul total mediu este descrescator. Daca costul marginal este superior costului mediu (costul variabil mediu), acesta este crescator. Atat timp cat costul marginal este inferior costului total mediu, el trage pe aceasta din urma in jos. Cand C_mg=C_TM acesta din urma nici nu urca nici nu coboara, dar se situeaza la nivelul sau minim. Din momentul in care C_mg devine superior lui C_TM el il trage pe acesta, in sus. De aici rezulta doua reguli:

a)   daca o curba a costului marginal este situata sub curba costului total mediu care ii este asociata, prima trage curba C_TM spre in jos; daca curba costului marginal C_mg este situata deasupra curbei C_TM, prima trage pe cea de-a doua in sus; daca C_mg=C_TM, atunci curba costului total mediu este in mod necesar o dreapta orizontala.

b)   daca curba costului total mediu este o linie dreapta, curba costului marginal va fi o linie dreapta pornind din acelasi punct ca si curba C_TM dar cu o inclinare dubla fata de aceasta. Rezulta ca costul marginal este egal cu costul total mediu (costul variabil mediu) in cazul unui volum de productie pentru care costurile totale medii (costurile variabile medii) nu sunt nici crescatoare, nici descrescatoare, ceea ce indica existenta unui punct minim al curbei U a costului total mediu (costul variabil mediu), adica:

C_mg=C_TM minim

In punctul minim al costului total mediu este admisa egalitatea dintre costurile marginale si costul total mediu. Productia realizata cu costuri totale medii minime este o productie optima pentru producator (in functie de cost), dar nu este productia maxima. Depasirea acestui nivel de productie este posibil insa cu o crestere a costurilor totale medii si o crestere accelerata a costurilor marginale.

3 Forma curbei costului marginal

Precizarea formei curbei costului marginal, implica determinarea prealabila a formei matematice a functiei de cost total.

Daca consideram ca exista o stricta proportionalitate intre costul variabil si volumul productiei (fig.5.5), atunci avem

C_V = a.q

functia de cost variabil este liniara (a este factor de proportionalitate), iar:

C_T = C_V + C_F = aq + C_F

In acest caz, curba C_FM (C_F/q) este o ramura de hiperbola echilaterala avand ca asimtote axele coordonatelor, dar celelalte curbe sunt modificate in raport cu fig.5.4.

Costul marginal:

este constant si egal cu costul variabil mediu:

.

Curba costului marginal si curba costului variabil mediu se confunda intr-o dreapta paralela cu axa cantitatilor.

Curba costului mediu este o curba mereu descrescatoare

sub forma unei ramuri de hiperbola echilaterala avand ca asimptote axa ordonatelor si dreapta costului marginal (cost variabil mediu).

Ipoteza unor costuri crescatoare cu raze sistematic variabile in functie de nivelul productiei sta la baza graficului 5.4, ce are un caracter mai general, in sensul ca indica ansamblul cazurilor posibil. Ipoteze alternative sunt cele care presupun o stricta proportionalitate a costului in raport cu volumul productiei si a liniaritatii 'pe intervale'5.

Este posibil ca pentru un proces de productie determinat, curbele din fig.5.4 sa nu fie valabile decat partial, costul marginal nu poate fi descrescator.

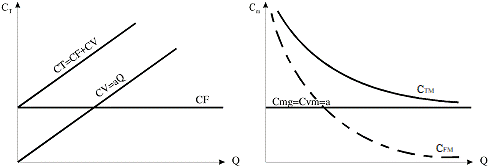
Fig.5.5. Curbe de cost in cazul unei functii liniare.

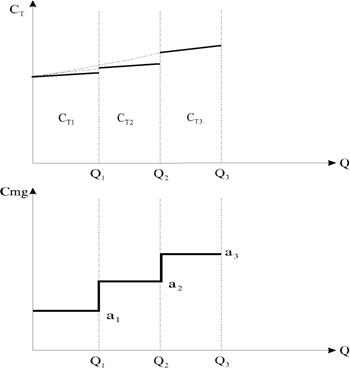
Fig.5.6 Curbe de cost pentru o functie liniara pe intervale.

De asemenea, functia costului variabil nu poate fi liniara pentru orice nivel al productiei. Este posibil ca la un anumit nivel sa apara dificultati suplimentare pentru un producator si are loc o crestere mai mult decat pro­portionala a costurilor. In acest caz functia de cost este 'liniara pe inter­vale' (fig.5.6). Pentru un nivel de productie Q<Q₁, C_T=a₁Q+C_F1. La nivelul productie Q₁ apare o 'ruptura', adica costurile cresc mai repede si pentru Q₁< Q< Q₂ exista o functie de cost total C_T2=a₂Q+C_F2, unde a₂> a₁.

Acest proces genereaza o curba in trepte ce evidentiaza evolutia costurilor marginale crescatoare. Daca avem in vedere o infinitate de procese de productie puse in functiune in mod succesiv la intervale de productie tot mai restranse, curba 'in trepte' devine o curba continua, curba J (fig.5.7).

Fig.5.7 Curba J a costului marginal

In mod obisnuit, curba costului marginal este o curba U, in care partea descrescatoare este expresia ipotezei randamentelor crescatoare. In cazul curbei J, traiectoria se explica prin ipoteza inexistentei randamentelor crescatoare.