Simularea structurilor rezistive

Simularea structurilor rezistive

Desfasurarea lucrarii:

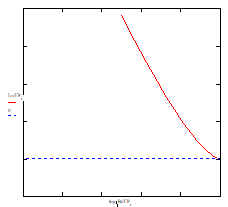
1.                 Apelam fisierul SOLTREZ.MCD din programul Mathcad, si introducem datele: R_n=10 kΩ, P_n=0,5 W, U_max=350 V, θ_n=70°C, θ_max=130°C. Programul reprezinta grafic puterea disipata, in functie de temperatura ambianta P_d(θ), aceasta functie avand ecuatia:

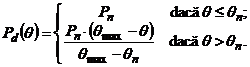
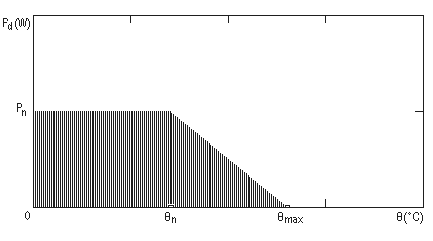
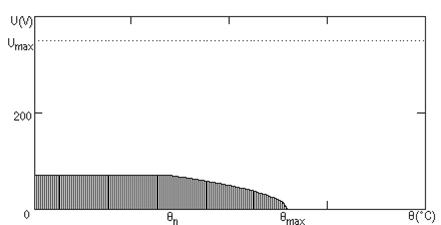
Nota: pentru graficele de mai sus, ca si pentru cele care vor urma, valorile acceptabile pentru parametrii figurati sunt cele aflate in aria hasurata a graficelor.

2.                 In continuare programul a calculat valoarea rezistentei critice. Rezistenta critica este acea valoare a rezistentei unui tip de rezistor pentru care tensiunea maxima de folosire este egala cu tensiunea pentru care se disipa puterea maxima, la temperaturi mai mici decat cea nominala. Rezistenta critica se calculeaza dupa formula:

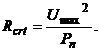
In cazul datelor introduse la punctul 1, valoarea rezistentei critice este R_crt=2,45∙10⁵ Ω, adica R_crt=245 kΩ.

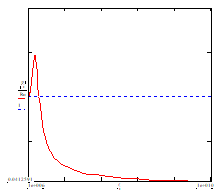
3.                 In cele ce urmeaza, vom analiza situatia R_n=R_crt. Graficele P(θ) si U(θ) arata dupa cum urmeaza:

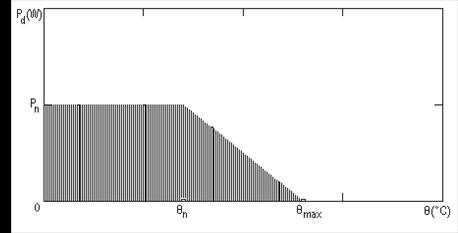
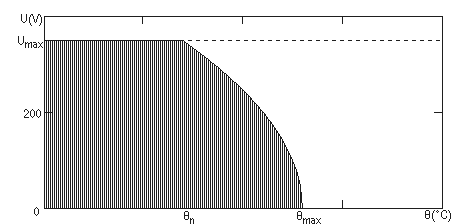
Observam ca graficul P(θ) este acelasi pentru orice valori ale rezistentei R_n (este normal, deoarece puterea maxima disipata este independenta de rezistenta nominala). Din acest motiv nu il vom mai figura si pentru celelalte doua cazuri (R_n>R_crt si R_n<R_crt). Graficul tensiunii maxime admisibile ca functie de temperatura are portiunea orizontala (pana la temperatura nominala) la acelasi U ca si U_max.

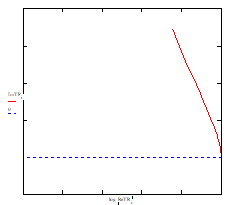
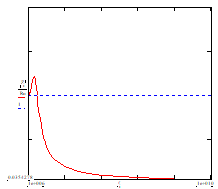
4.                 In cazul in care R_n<R_crt, graficul U(θ) este asemanator cu cel de la punctul 1.Tensiunea maxima pe care o putem aplica rezistorului este limitata doar de puterea maxima pe care o poate acesta disipa. Valoarea rezistentei rezistorului pentru care am trasat graficul corespunzator este de R_n=24,5 kΩ.

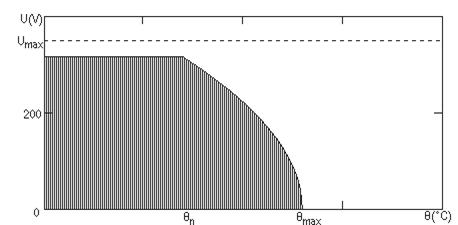
5.                 Daca R_n>R_crt limitarea tensiunii se va face pe o portiune datorita valorii tensiunii maxime pe care o suporta rezistorul, iar pe cea de-a doua portiune de catre valoarea puterii disipate maxime. Valoarea rezistentei rezistorului a fost aleasa, pentru acest caz, de R_n=2,45 MΩ.

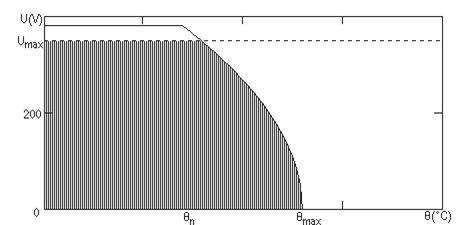
6.                 TEMA 1:

Dupa parcurgerea problemei rezolvate, prezentate atat in fisierul SOLTREZ.MCD cat si in indrumarul de laborator am rezolvat prima problema propusa. Cele trei rezistoare considerate au parametrii:

Am calculat, pentru inceput, valorile rezistentelor critice pentru cele trei rezistoare cu formula:

,

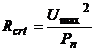din care R_crt1=250 kΩ, R_crt2=125 kΩ, R_crt3=245 kΩ. Apoi, folosind programul Mathcad, reprezentam grafic tensiunea (U) ca functie de temperatura (θ).

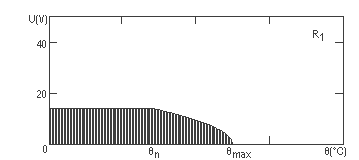
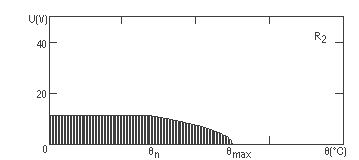
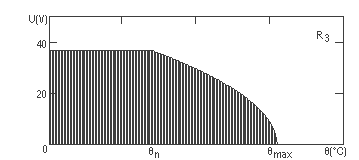
Observam ca limitarea tensiunilor este datorata exclusiv puterilor maxime pe care le pot disipa rezistoarele. Intervalul de temperaturi in care sunt folosite rezistoarele este de [0,110]°C. Pe acest interval de temperaturi valorile minime pentru tensiunile maxime aplicabile sunt pentru θ=110°C, acestea fiind: U_a1=7,39 V, U_a2=5,84 V, U_a3=26,73 V. Deoarece cele trei rezistoare sunt legate in paralel, tensiunea maxima pe care o putem aplica gruparii este U_a=min(U_a1, U_a2, U_a3). Avem deci U_a=5,84 V.

7.                 Tema 2:

Studiem domeniul maxim admisibil pentru curentul care strabate o grupare serie a rezistoarelor de la punctul precedent. In acest scop am modificat fisierul SOLTREZ.MCD; am introdus calculul valorii maxime a curentului prin rezistoare:

Astfel, valorile maxime ale curentilor prin cele trei rezistoare sunt: I_max1=2,5 A, I_max2=0,125 A, I_max3=0,l29 A. Apoi, am scris formula intensitatii maxime admisibile pentru fiecare rezistor, ca fiind:

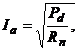
unde P_d=P_n, pentru θ≤θ_n, si P_d=P_n∙( θ_max-θ)/(θ_max-θ_n). In cele din urma, am reprezentat grafic functiile I_a1(θ), I_a2(θ) si I_a3(θ).

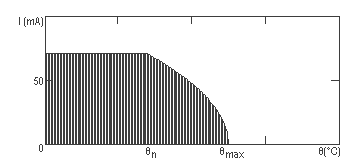
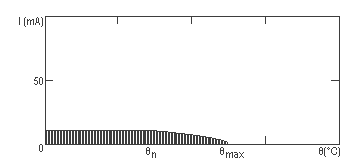
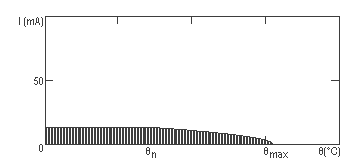
In intervalul de temperatura in care functioneaza rezistoarele ([0,110]°C), minimele curentilor maximi admisibili sunt la temperatura de 110°C, acestea fiind: I_a1=36,9 mA, I_a2=5,83 mA, I_a3=9,90 mA. Deoarece cele trei rezistoare sunt conectate in serie, valoarea curentului care trece prin ele este aceeasi. Aceasta valoare este I_a=min(I_a1, I_a2, I_a3), deci I_a=5,83 mA.

8.                 In continuare am incarcat fisierul SOLIMP.MCD, pentru a studia solicitarea in impuls a rezistoarelor. In prima parte am analizat incalzirea, respectiv racirea corpului rezistoarelor de tip RCG, avand diferite valori. Pentru acest tip de rezistoare avem θ_max=130°C, θ_n=70°C, si consideram temperatura ambianta θ_a=20°C si temperatura initiala a rezistoarelor θ_i=100. Cele trei rezistoare pe care le vom analiza sunt RCG 1100, RCG 1025 si RCG 2012, avand masele m₁=1,80 g, m₂=0,25 g, m₃=0,24 g, si caldura specifica c=0,5 J/gK. Rezistoarelor le aplicam o putere P=1 W, timpul de simulare fiind de 100 s. Programul calculeaza capacitatile termice C_th, rezistentele termice R_th si constantele de timp τ_th.

τ₁=54 s, τ₂=7,5 s, τ₃=7,2 s.

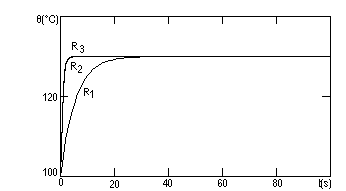
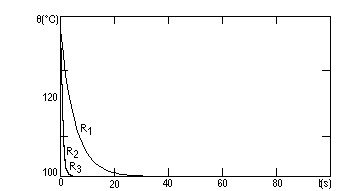
Cu valorile obtinute pentru fiecare rezistor se traseaza graficul temperaturii corpului rezistoarelor ca functie de timp, la incalzire si la racire.

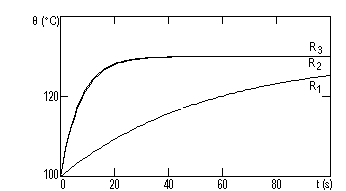
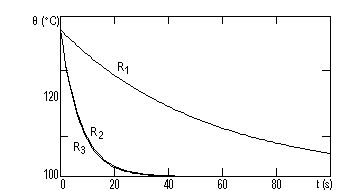
Observam faptul ca τ, constanta termica, influenteaza viteza de variatie a temperaturii. Astfel, pentru τ mare, componenta ajunge mai greu la temperatura de echilibru.

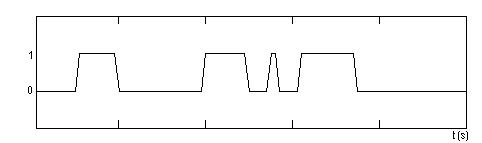
9.                 In cazul aplicarii unui tren de impulsuri, au loc mai multe etape de incalzire si racire succesive. In graficele de mai jos se observa foarte clar influenta constante termice asupra procesului de incalzire a rezistoarelor. Primul grafic prezinta forma si durata impulsurilor, al doilea temperatura primului rezistor (avand constanta termica mare) iar cel de-al treilea prezinta temperatura rezistorului R₂ (avand constanta termica comparabila ca valoare cu durata impulsurilor), cele trei grafice avand aceeasi scara de timp.

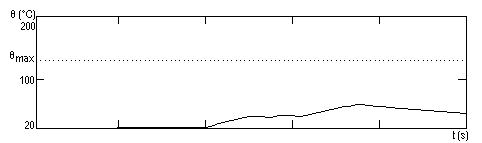
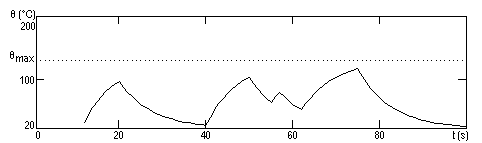
10.            Deoarece constanta termica este invers proportionala cu puterea aplicata, cresterea puterii de 10 ori atrage dupa sine o scadere de 10 ori a constantei termice τ. Astfel, noile constante termice vor fi: τ₁=5,4 s, τ₂=0,75 s, si τ₃=0,72 s. Din aceasta cauza, si timpii de atingere a temperaturii de echilibru sunt mult mai mici. Prezentam in continuare graficele corespunzatoare aplicarii unei puteri P=10 W, pe un interval de timp de 100 s.

In cazul aplicarii trenului de impulsuri de la punctul precedent, comportarea rezistoarelor este ca in graficele urmatoare:

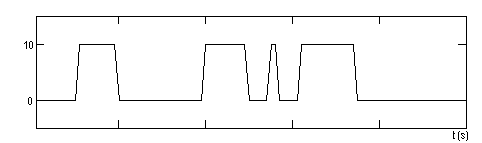
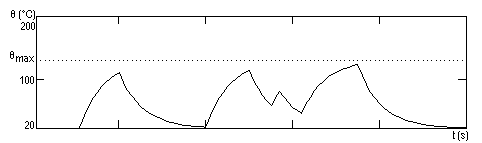
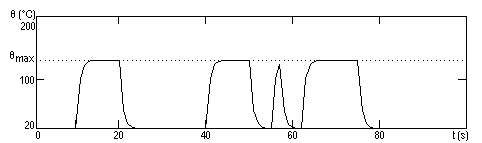
11.            Constanta de timp pentru rezistorul corespunzator graficului anterior, caruia ii este aplicata o putere P=10 W, este τ₂=0,75 s. Se observa ca aceasta constanta de timp este mult mai mica decat durata unui impuls al semnalului aplicat (t_i>3τ). Din acest motiv se pot observa pe grafic domeniile de stabilitate pentru trei din impulsurile semnalului.

12.            Dupa incarcarea programului SOLFRCV.MCD am obtinut urmatoarele grafice pentru R<R_C:

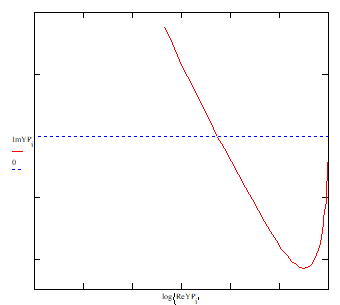
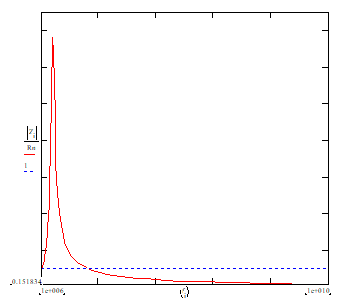
13.            Apoi am calculat R_C pentru care nu se manifesta caracter inductiv: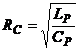. R_C=1,288 kΩ. Apoi am reprezentat aceleasi grafice pentru R=R_C si R>R_C.