Variabile de acceleratii pe o cale cu abateri de la dimensiunile nominale

Variabile de acceleratii pe o cale cu abateri de la dimensiunile nominale

Ca in orice sistem tehnic, calea trebuie sa aibe tolerante de executie si intretinere, ale caror limite sa permita functionarea acceptabila a sistemului general vehicul - cale.

Abaterile de la dimensiunile nominale, intr-un punct oarecare al curbei, se definesc astfel:

- abaterea de suprainaltare sau de nivel transversal

Δ h_x

unde H^* este suprainaltarea reala si h_x - suprainaltarea nominala;

- abaterea de raza

Δ R_x = R_x - R_x^*

unde R* este raza de curbura reala si R_x - raza de curbura nominala. Din relatia anterioara se poate exprima abaterea de curbura

Δ k_x = 1 / R²_x - 1 / R_{x =} Δ R_x / (R_x R_x^*)

Insuficienta de suprainaltare intr-un punct oarecare al curbei va fi:

I_x^* = 11,8 V²/R_x^* - h_x^* - 11,8 V² (Δ k_x + 1/R_x)-( Δh_x + h_x)=

=I_x + 11,8 V²Δk_x - Δh_x

unde- I_x = 11,8 V²/R_x h_x reprezinta insuficienta de suprainaltare nominala.

Expresia pe langa faptul ca este valabila atat pe curba circulara, cat si pe racordare, prezinta avantajul ca se preteaza la o reprezentare grafica clara (fig...), in analogie cu diagramele de nivel si de sageti (proportionate cu curburile) ale inregistrarilor efectuate cu vagonul de verificat calea. Sensurile algebrice ale abaterilor sunt cele rezultate din relatiile ... Se constata ca insuficienta maxima de suprainaltare, deci situatia cea mai defavorabila, se ob|ine pentru valorile pozitive ale abaterii de curbura si pentru cele negative ale abaterii de suprainaltare.

Intre doua puncte consecutive, distantate cu Δl = x₂ - x₁ [m], diferenta de suprainaltare sau torsionarea caii este data de relatia

t_c=ΔH^*=h₂^* - h₁^* + (h₂ - h₁)+(Δh₂ -Δh₁)= ΔH + (Δh₂ -Δh₁) [mm]

Marimea

g = t_c / Δl = ΔH /Δl +(Δh₂ -Δh₁ )/Δl [mm/m]

defineste, ca si pe racordare, panta suprainaltarii sau panta de torsionare a caii. Relatia arata ca panta contine un termen constant

ΔH /Δl =h /L = p [mm/m],

care reprezinta panta suprainaltarii nominale pe racordare, iar al doilea termen

(Δh₂ -Δh₁ )/Δl [mm/m]

reprezinta o panta suplimentara care depinde de marimea abaterilor de suprainaltare (adancimea denivelarilor) Δ h, de distributia acestora de-a lungul caii si este influentata de baza de masura Δl .

Relatia exprima deci legea de regresie a pantei de torsionare functie de baza de masura, care de regula este neliniara.

Panta suprainaljarii p se poate modifica prin 'caderea' firului interior al caii datorita traficului intens al trenurilor de marfa care circula, asa cum s-a aratat, cu exces de suprainaltare sau a firului exterior al caii datorita unui trafic intens al trenurilor de calatori care circula cu insuficienta de suprainaltare.

Comitetul ORE B 55, in urma statisticilor efectuate pe diferite retele europene privind torsionarile care pot fi intalnite in cale, a stabilit relatii care definesc valorile.

Limita ale pantelor de torsionare, functie de baza de masura Δl.

Intre doua puncte consecutive distantate cu Δ_l , diferenta de curbura este data de relatia

ΔK*= 1/R₂*-1/R₁* = (1/R₂-1/R₁) + (1/R₂*-1/R₂) - (1/R₁*-1/R₁) =

=ΔK+(Δk₂-Δk₁)

iar marimea    ΔK*/Δl = ΔK/Δl + (Δk₂-Δk₁)/ Δl

defineste variatia spatiala a curburii.

Relatia arata ca variatia curburii contine, de asemenea, un termen constant

ΔK/Δl  =(1/R₂-1/R₁) /Δl

apartinand variatiei nominale a curburii pe racordare, iar termenul

(Δk₂-Δk₁)/ Δ_l

depinde de marimea abaterilor de curbura Δk , de distributia acestora de-a lungul caii, fiind influentat de baza de masura. In curba circulara actioneaza numai acest termen.

Relatia exprima deci legea de regresie a curburilor functie de baza de masura care, de asemenea, este neliniara.

Variatia insuficientei de suprainaltare intre doua puncte este

ΔI* = I₂* - I₁* = I₂ - I₁ + 11,8V₂ (Δk₂-Δk₁) - (Δh₂-Δh₁)

sau, raportata la baza longitudinala de masura,

ΔI*/ Δl = ΔI/Δl +11,8V₂(Δk₂-Δk₁)/ Δl - (Δh₂-Δh₁)/ Δl

care reprezinta variatia spatiala a insuficientei de suprainaltare, de asemenea dupa o lege de regresie neliniara in raport cu baza de masura.

Observand fig.., se constata ca situatia cea mai defavorabila, care conduce la cea mai mare variatie a insuficientei de suprainaltare si totodata la insuficienta maxima de suprainaltare, apare la intrarea vehiculului pe racordare cand panta supraina1tarii are valoarea maxima negativa si variatia curburii valoarea maxima pozitiva.

Daca intr-o astfel de situatie

Δk₂= - Δk₁ = Δk si Δh₂ = -Δh₁ = -Δh /2,

atunci

ΔI*/ Δl = ΔI/Δl +(11,8V₂)2 (Δk/ Δl) +( Δh/ Δl)

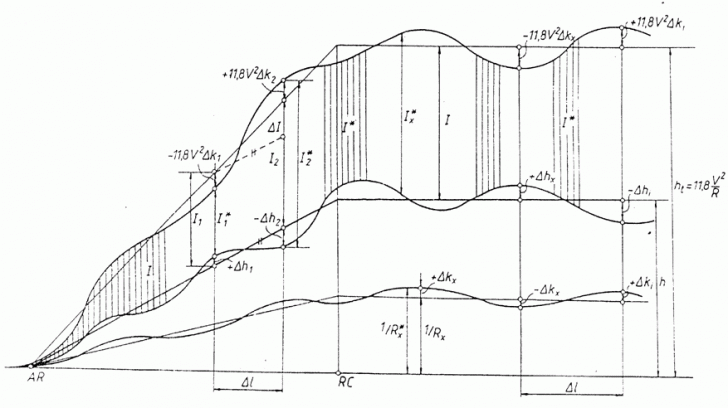
Fig... Parametrii cinematici la circulatia vehiculului in curbe cu abateri de la dimensiunile nominale

Variatia insuficientei dc suprainaltare ΔI*/ Δl caracterizeaza coturile care apar in cale. Coturile de acest gen, caracterizate printr-o simpla variatie a insuficienjei de suprainaltare rezultata din suprapunerea abaterii de la curbura peste panta torsionarii, constituie asa - zisele coturi continue

In dreptul joantelor, din cauza diferentei de momente de inertie la eclise fata de sina, pot sa apara si coturi discontinue, caracterizate prin unghiul de soc care se formeaza intre tangentele la cele doua curbe in punctul de discontinuitate.

Existenta coturilor discontinue in cale nu este acceptata sub nici o forma

Evenimentele de cale ferata care s-au produs au aratat ca acestea genereaza forte de deripare de 10 20 ori mai mari decat cele cvasistatice, in functie de marimea unghiului de soc, mai ales daca sunt asociate cu valori maximale tolerate pentru coturile continue.

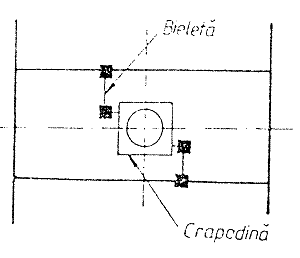
Fig. Schema de principiu a antrenarii pivotului prin "lemnicata"

Variatia insuficientei de suprainaltare ΔI*/ Δl produce smucirea transversala a vehiculelor. Variatia de acceleratie transversala imprimata vehiculului este

in care, daca se inlocuieste ΔI*/Δl , rezulta corelatia dintre abaterile de curbura si de suprainaltare, functie de Δ_γ T₀/Δ_t admis.

La circulatia vehiculului, datorita abaterilor, apar socuri transversale care pot fi transmise vehiculului o data cu consumarea jocurilor dintre-traversa dansanta si cadrele boghiului. O solutie, care este aplicata la boghiurile de mare viteza si care elimina complet limitatorii, consta in antrenarea pivotului 'prin lemniscata' (fig...). Silentblocurile bieletelor permit pivotului o deplasare in forma de ∞ (lemniscata) si deci o preluare elastica a socurilor.