Studiul ductilitatii cadrelor metalice portal - hala metalica

STUDIUL DUCTILITATII CADRELOR METALICE PORTAL - HALA METALICA

1 Introducere

Structurile sunt proiectate uzual astfel incat o parte din energia inmagazinata in timpul cutremurelor puternice sa fie disipata prin deformatii inelastice . Pentru prevenirea colapsului structurii, valorile acestor deformatii plastice trebuie limitate in conformitate cu ductilitatea locala si globala a structurii si cu capacitatea de disipare a energiei.

In cazul utilizarii metodei la stari limita, proiectarea antiseismica a structurilor poate fi realizata in prezent prin intermediul a doua metode de analiza structurala. Prima metoda foloseste analiza dinamica neliniara care poate furniza cu un grad suficient de acuratete raspunsul in timp al structurii la actiunea unor cutremure. Cea de-a doua metoda se bazeaza pe analiza modala in domeniul elastic utilizand un spectru de proiectare, care furnizeaza, functie de perioada T, pseudo-spectrul normalizat al acceleratiei, necesar pentru un anumit nivel al raspunsului inelastic Aceste spectre inelastice se obtin in normele de proiectare antiseismica modificand spectrul de raspuns elastic de proiectare prin intermediul factorului q, care ia in considerare capacitatea structurii de disipare a energiei.

Evaluarea corecta a factorului q, care poate fi definit ca raportul dintre valoarea acceleratiei care conduce la cedarea structurii si valoarea acceleratiei corespunzatoare formarii primei articulatii plastice, necesita realizarea unor analize dinamice pentru diferite tipuri de miscari seismice. Performantele globale seismice ale cadrelor metalice portal pot fi evaluate printr-o analiza neliniara inelastica de tip pushover. Pentru analiza neliniara pushover, cadrele sunt incarcate cu o forta orizontala crescatoare (Figura 1), acesta deformandu-se lateral in functie de magnitudinea fortei aplicate.

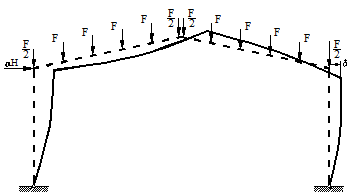
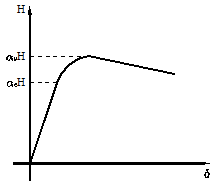
Figura 1 - Analiza inelastica Pushover

Sub actiunea fortei orizontale, structura se comporta elastic pana la aparitia primei articulatii plastice corespunzator factorului de amplificare α_e, dupa care structura se comporta inelastic pana la colapsul acesteia.

2 Cadrele studiate si metodele de analiza

Au fost studiate patru cadre, avand aceiasi deschidere si inaltime, dar doua pante diferite. Toate cadrele au rigle vutata si stalpi cu sectiune constanta sau variabila. Mai multe detalii sunt prezentate in Tabelul 2.1.

Cazul 1C corespunde stalpilor cu sectiune variabila cuprinsa intre Clasa 1 si Clasa  3C reprezinta cazul cu stalpi constanti de Clasa 1. Riglele au sectiuni intre Clasa 1 si 3 in toate cazurile. Otelul utilizat este S235.

Analizele efectuate sunt urmatoarele: analiza 2D statica elasto-plastica, analiza 2D neliniara time-history, analiza 3D statica elasto-plastica. Analizele 2D au fost realizate cu programul Drain 3DX, iar analizele 3D cu programul de elemente finite ANSYS. In cazul programului Drain 3DX, cadrele au fost modelate cu elemente de tip fibra, iar in cadrul analizelor in ANSYS, au fost utilizate elemente SHELL4 In ambele analize a fost considerat un material avand un comportament biliniar elasto-plastic. In analizele 3D, au fost considerate blocaje laterale ale riglei datorate panelor [1]. Blocajele laterale sunt de 4 tipuri ( Figura 2.5) si anume: tipul 1 - fara blocaje laterale, tipul 2 - blocarea deplasarii laterale, tipul 3 - blocarea deplasarii laterale cat si a rotirii, tipul 4 - blocarea deplasarii laterale dar si a deplasarii laterale a talpii comprimate (in punctele in care se dispun contrafise).

Imbinarea rigla-stalp este rigida conform Figurii 2.4. Pentru analizele 2D capacitatea si rigiditatea la rotire a imbinarii rigla-stalp cat si prinderea stalpului la baza au fost evaluate in conformitatea cu metoda componentelor din EN 1993-1-8 [2]. In cadrul analizelor 3D imbinarea rigla-stalp si prinderea stalpului la baza a fost modelata utilizand elemente de contact.

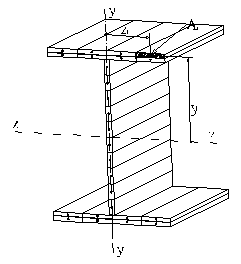
Figura 2 Sectiune dublu T modelata cu elemente de fibra

Modelarea cu elemente de tip fibra a unei sectiuni dublu T este prezentata in Figura 2. Sectiunea elementului a fost impartita intr-un numar de fasii, concentrand proprietatile fiecarei fasii in centru ei de greutate.

3 Ductilitatea cadrelor portal

Metoda spectrului de capacitate

Metoda spectrului de capacitate compara capacitatea efectiva a structurii cu cerinta de capacitate indusa de miscarea seismica. Relatia intre capacitatea efectiva si cea necesara poate fi reprezentata utilizand doua metode: (1) un raspuns spectral liniar-elastic cu o amortizare ridicata; (2) raspuns spectral inelastic. Cum s-a putut observa si din paragraful anterior, cadrele metalice portal sunt caracterizate printr-o clasa de ductilitate redusa spre medie, fiind recomandata prima metoda. In consecinta, capacitatea spectrala necesara a structurii, ca efect a miscarii seismice, poate fi construita prin trasarea spectrului acceleratie, linear elastic , S_a, pentru un sistem cu un singur grad de libertate raportat la spectrul deplasarilor, S_d, pentru o valoare data a amortizarii vascoase, ξ. Acesta se va trasa utilizand formula:

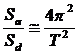
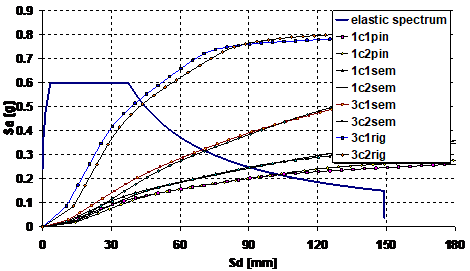
Figura 3 Spectrul de capacitate

Forta laterala si capacitatea de deplasare a structurii vor fi reprezentate utilizand relatia forta-deplasare globala (F-Δ) obtinuta in urma unei analize neliniare de tip "pushover". Presupunand ca raspunsul seismic global al structurii este dat de primul mod fundamental de vibratie, curba pushover poate fi convertita intr-o relatie acceleratie-deplasare idealizata (a^*-Δ^*), corespunzatoare unui sistem cu un singur grad de libertate, dupa cum urmeaza:

unde m^* reprezinta masa unui sistem echivalent cu un singur grad de libertate, iar Γ este factorul de participare global [4]. Relatia a^*-Δ^* (curba de capacitate) este trasata impreuna cu spectrul S_a-S_d, pentru o valoare a amortizarii vascoase ξ=5%, in Figura  Punctele de intersectie ale celor doua curbe reprezinta acceleratia si deplasarea necesara unei proiectari antiseismice. Aceste valori corespunzatoare deplasarii, vor fi luate in considerare in continuare pentru a stabilii starea limita a structurii.

Performante seismice, factorul q

Performantele seismice globale a cadrelor au fost evaluate utilizand o analiza statica neliniara, echivalenta (analiza push-over) si o analiza neliniara time-history. Analizele push-over au fost realizate pe cadre spatiale, analize in cadrul carora au fost simulate, individual, toate cele patru tipuri de blocaje laterale (vezi Figura 2.5). Forta seismica fiind evaluata in conformitate cu prevederile EC8. In cazul analizelor neliniare time-history, a fost utilizata accelerograma unui seism.

In conformitate cu prima metoda, factorii q, calculati utilizand equatia de mai jos, sunt trecuti in Figura 4.

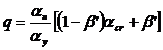
unde:

T - este perioada fundamentala de vibratie;

α_cr - este factorul critic elastic de multiplicare a fortelor gravitationale (α_cr=V_cr/V);

α_u - factorul de multiplicare a fortelor orizontale corespunzatoare colapsului structurii;

α_y- factorul de multiplicare a fortelor orizontale corespunzatoare primei articulatii plastice.

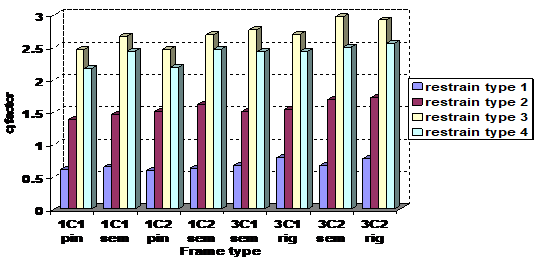
Figura 4 Valorile factorului q calculate cu ecuatia

Valoarea factorilor q din Figura 4, confirma valorile prevazute in EN 1998-1 [5] pentru structuri nedisipative (q=1.5). De asemenea, se poate concluziona ca, cadrele metalice portal, ar trebui proiectate in conformitate cu conceptual de structura slab disipativa pentru care q ia valori intre 1.5 si 2.5. De asemenea redundanta si supra rezistenta structurii, datorate prinderii laterale si a modului de prindere a stalpului la baza au un rol important. Valorile subunitare obtinute pentru tipul de prindere 1, q<1, se datoreaza efectului dominant pe care P_cr il are in Eq. (3). Structurile mentionate, nu sunt prinse lateral, fiind foarte sensibile la fenomenul de instabilitate. Sub actiunea seismica ele ar ceda prematur prin instabilitate dinamica.

Factorul q, a fost calculat si prin intermediul unei analize neliniare time-history, care este mult mai apropiat de definitia lui reala (raportul dintre factorul corespunzator colapsului structurii si cel corespunzator atingerii limitei de curgere). Accelerograma folosita in cadrul analizei neliniare dinamice este El Centro Site Imperial Valley Irrigation District Comp S00E (Fig. 5).

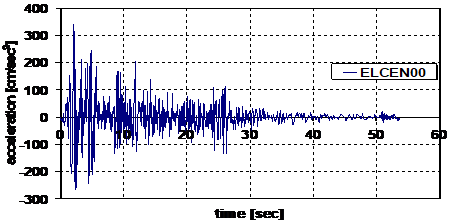
Figura 5 Accelerograma (ELCEN S00E)

Trebuie subliniat ca nu a fost inregistrat colapsul structurii in nici unul din cazuri. In aceste conditii colapsul teoretic a fost considerat deplasarea corespunzatoare spectrului de capacitate pentru proiectarea structurii. Astfel valoarea factorului de reducere a miscarii seismice, calculat ecuatia de mai jos), este prezentat in Figura 6.

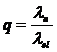
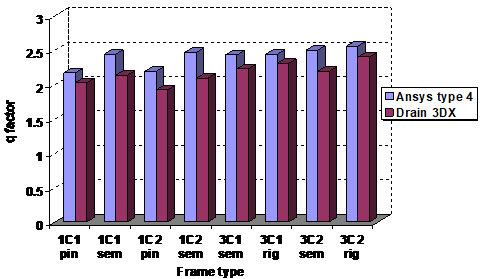
Figura 6 Comparatie factorul q Ansys-Drain 3DX

Din Figura 7, putem observa ca valorile obtinute din analiza dinamica sunt de nivelul celor din analiza neliniara statica, in care a fost simulat tipul de prindere 4, insa valorile sunt ceva mai mici.

4 Cazuri practice de proiectare

Rezultatele prezentate pana in momentul de fata s-au referit la un numar de cadre calibrate pe baza unor teste de laborator. Acestea fiind alese ca fiind oarecum echivalente cu cadrele testate, pastrand aceiasi deschidere, inaltime si panta a acoperisului. In continuare vor fi prezentate rezultatele obtinute pentru un numar de cadre utilizate in proiectarea curenta (Figura 2.9). Acestea au deschideri diferite inaltimi diferite si panta acoperisului de 8^o. Toate cadrele au stalpii cu sectiune variabila, iar riglele cadrului sunt vutate pe o lungime 0.15L, imbinarea rigla stalp fiind considerata rigida, rigla prinzandu-se pe capul stalpului. Prinderea in fundatie a acestor tipuri de cadre s-a considerat a fi articulata (Figura 7). Proiectarea acestora s-a realizat tinandu-se cont de ipotezele de incarcare permanenta si zapada (ipoteze care conduc la combinatia cea mai defavorabila), rezultand in final sectiunile prezentate in Tabelul 2.

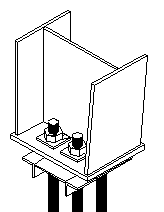
Figura 7. Prinderea articulate a stalpului la baza

Pentru determinarea incarcarilor aferente ipotezelor de calcul au fost considerate urmatoarele cazuri de incarcare:

• incarcare permanenta g_p=1.5 kN/m
• incarcare din zapada   g_z=7.2 kN/m (Bucuresti)

Combinatia de incarcare folosita a fost:

unde

• coeficientul partial de siguranta n=1.1
• coeficientul partial de siguranta n_z=2.1

Performante seismice, factorul q

Pentru determinarea factorilor care intra in ec. (3) au fost realizate: analize pushover plane (determinarea factorilor α_u si α_y, cat si pentru identificarea pozitiei articulatiilor plastice punctuale in acest caz), analize modale (pentru identificarea perioadelor corespunzatoare primului mod de oscilatie), analize elastice de flambaj spatiale ( pentru determinarea factorului critic de flambaj α_c).

Analizele plane s-au realizat cu programul Sap2000 , care opereaza numai cu elemente de tip bara, iar analizele 3D au fost realizate cu programul de elemente finite ANSYS, in cadrul caruia discretizarea cadrelor s-a realizat cu ajutorul elementelor de tip "shell". In ambele analize s-a considerat un comportament bilinear, elastic-perfect plastic, al materialului. S-a utilizat OL37 (S235), cu limita de curgere f_y=235 N/mm². In cazul analizei 3D, deplasarile laterale ale riglelor si stalpilor cadrului s-au considerat blocate la talpa exterioara a elementului de catre de riglele de perete, panele de acoperis si contrafise la talpa inferioara in unele cazuri. S-au simulat patru tipuri de blocaje laterale. (Figura 2.5)

Rezultatele analizelor prezentate anterior sunt trecute in tabelul 1:

Tabelul 1: Rezultatele analizelor

Factorii q calculati conform Eq (3), utilizand valorile din Tabelul 1 sunt prezentati in figura 8, pentru fiecare tip de cadru in parte.

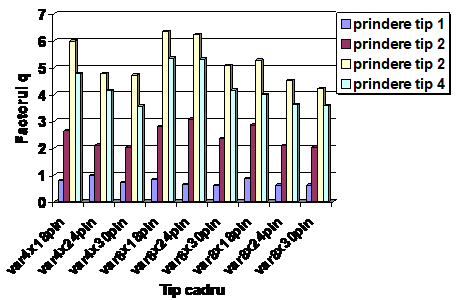
Figura 8 Factori de reducere a incarcarii seismice