MECANICA MOLECULARA - Definirea campului de forta in mecanica moleculara

MECANICA MOLECULARA

Mecanica moleculara a aparut si s-a dezvoltat ca o necesitate pentru descrierea structurii si proprietatilor moleculare, in primul rand pentru molecule foarte mari, pentru care metodele mecanicii cuantice nu pot fi aplicate datorita, pe de o parte, capacitatii limitate a tehnicii de calcul actuale cat si timpului de calcul extrem de mare necesar aplicarii unor astfel de metode.

Domeniile de aplicabilitate a mecanicii moleculare includ:

starea fundamentala a moleculelor

luarea in considerare in mod explicit a efectului de solvent

molecule continand mii de atomi: oligonucleotide, peptide, poli-zaharide

compusi organometalici si anorganici limitat

proprietati termodinamice si cinetice via dinamica moleculara

Marele avantaj al mecanicii moleculare este viteza mare de calcul, ceea ce permite folosirea ei in tehnici si proceduri care necesita un numar foarte mare de evaluari ale energiei moleculelor, cum ar fi optimizarea geometriei moleculare, studiul conformational, docarea moleculara, dinamica moleculara, etc.

Acuratetea mecanicii moleculare in descrierea proprietatilor moleculare, depinde de baza de date utilizata in parametrizarea metodei; diferitele variante ale mecanicii moleculare dau, de obicei, rezultate bune pentru o anumita clasa de molecule pentru care metoda a fost parametrizata. Un mare dezavantaj al acestor metode este tocmai necesitatea acestei parametrizari, fara de care calculul nu poate fi efectuat, parametrizare care este mare consumatoare de timp.

Definirea campului de forta in mecanica moleculara

Mecanica moleculara utilizeaza ecuatii ale mecanicii clasice pentru a descrie suprafetele de energie potentiala si proprietatile fizice ale moleculelor.

O molecula este descrisa ca o colectie de atomi care interactioneaza intre ei prin potentiale descrise de functii analitice clasice. Totalitatea acestor functii impreuna cu tipurile atomilor si parametrii corespunzatori, definesc asa numitul camp de forta.

Cu totul diferit de mecanica cuantica, mecanica moleculara nu trateaza electronii in mod explicit ci sunt inglobati in particule asemanatoare atomilor. Atomii sunt priviti ca sfere rigide avand raze fixe, obtinute fie teoretic, fie experimental si purtand sarcini nete obtinute teoretic. Legaturile chimice sunt considerate resorturi; fizica deformarii resortului va descrie capacitatea legaturilor chimice de a se intinde, deforma sau torsiona (modificarea unghiului diedru).

Atomii care se afla la o distanta mai mare decat doua legaturi sunt considerati nelegati si vor interactiona prin forte atractive de tip van der Waals, prin legaturi de hidrogen, prin repulsii sterice si prin forte electrostatice atractive sau repulsive in functie de sarcinile nete plasate pe atomi. Aceste interactii pot fi calculate fara dificultate atata timp cat atomii sunt considerati sfere cu raze caracteristice.

O ecuatie simpla a mecanicii moleculare se obtine prin insumarea diferitelor interactii prezentate in Figura

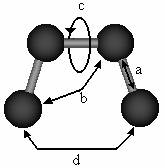
Figura Principalele tipuri de interactii incluse in campul de forta:

a. intinderea legaturii; b. deformarea unghiului de valenta

c. torsiunea legaturii; d. interactii intre atomii nelegati;

Ecuatiile care redau aceste interactii, impreuna cu parametrii necesari descrierii diferitelor tipuri de atomi si legaturi chimice reprezinta dupa cum s-a aratat, campul de forta.

In cadrul mecanicii moleculare au aparut si s-au dezvoltat cateva tipuri de campuri de forta care difera prin functiile matematice folosite in descrierea interactiilor si prin domeniul molecular de aplicare. Astfel diferite pachete de programe de tip HyperChem, Sibyl, Insight folosesc campurile de forta MM+, MM2, AMBER, OPLS, CHARMM (sau o implementare a acestuia in HyperChem BIO+). Unele campuri de forta includ termeni de energie aditionali care descriu alte tipuri de deformari; altele tin seama de cuplarea dintre deformarea si intinderea legaturilor adiacente in scopul imbunatatirii acuratetii modelului mecanic.

Scopul mecanicii moleculare este de a calcula energia asociata unei anumite conformatii moleculare. Cu toate acestea, energiile calculate de catre mecanica moleculara nu au in valoare absoluta nici o semnificatie fizica intrinseca.

Numai diferentele de energie intre doua sau mai multe conformatii au semnificatie. Energiile calculate pentru un conformer sunt corelate cu entalpiile de formare, desi acestea nu sunt entalpii intrucat in energia totala calculata nu sunt inclusi termeni care sa tina seama de miscarea termica moleculara si nici termeni care sa reflecte dependenta de temperatura a diferitelor contributii.

1 Energia de intindere a legaturii

Ecuatia care descrie intinderea legaturii chimice este aproximata cu cea a oscilatorului armonic si are la baza legea lui Hooke:

()

unde constanta de forta reflecta rigiditatea legaturii, este lungimea legaturii la echilibru, iar r distanta intre atomi.

Fiecarui tip de legatura (C - C, C - H, C=O, etc.) ii este asociata o pereche de parametrii si . Fiecare termen al ecuatia () reprezinta energiei de vibratie in jurul pozitiei de echilibru pentru un tip de legatura si este ecuatia unei parabole.

O mai buna aproximatie pentru energia de vibratie o reprezinta functia Morse:

      (II.2)

D fiind energia de disociere, iar a o constanta egala cu

Dupa cum se poate observa din Figura II.2, unde sunt reprezentate cele doua functii pentru legatura carbonil (pentru campul de forta AMBER: = 1,229 Å, D = 150 Kcal/mol , = 570 Kcal/mol Ų,) spre deosebire de functia armonica, functia Morse poate descrie disocierea legaturii la elongatii mari si creste mult mai rapid la distante mai mici decat distanta de echilibru. Aceste diferente devin importante in simularile dinamicii moleculare, cand energia termica furnizata moleculei o indeparteaza mult de pozitia de echilibru. Pe de alta parte, in jurul pozitiei de echilibru cele doua functii sunt asemanatoare si conduc la valori similare privind structurile de echilibru, functia armonica prezentand avantajul unei viteze mai mari de calcul si a unei parametrizari mai usoare.

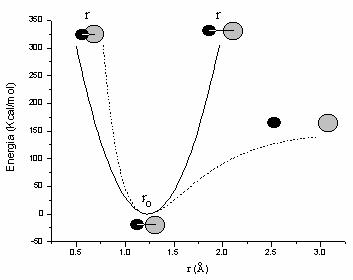
Figura II.2 Functia armonica ( ) si functia Morse (-----)

2 Energia de deformare a unghiului de valenta

Ecuatia energiei necesare deformarii unghiului de valenta are la baza tot legea Hooke:

          (II.3)

unde este constanta de forta asociata deformarii unui unghi de valenta, iar este unghiul de echilibru.

Termenii ecuatia (II.3) evalueaza energia asociata vibratiei unghiurilor de valenta in jurul valorilor de echilibru. In Figura II.2 este prezentata variatia energiei datorita deformarii unghiului C - C - C in alcani, de la valoarea sa de echilibru de 109,5^o (= 0,45 mdyn/Å rad² ).

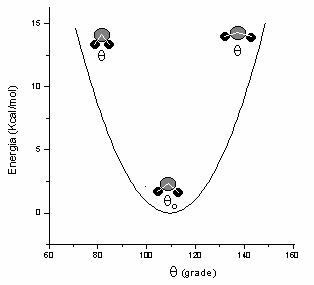
Figura II.3 Variatia energiei prin modificarea unghiului de valenta C - C - C

3 Energia de torsiune

Energia de torsiune este energia necesara modificarii unghiului diedru 1- 4, ceea ce echivaleaza cu rotirea in jurul unei legaturi cu unghiul . In mecanica moleculara functia potentiala corespunzatoare este simulata printr-o serie Fourier trunchiata:

                           (II.4)

Fiecare termen al ecuatiei (II.4) reprezinta o functie periodica in care sunt constante de forta, n este periodicitatea termenului Fourier, unghiul diedru, iar unghiul de faza.

Perioada interactiei este 360/n; pentru n = 1 si = 0, functia reprezinta situatia in care energia este minima pentru conformatia trans cu o bariera de V₁ pentru a trece in conformerul cis; un unghi de faza = 180 reprezinta situatia opusa cu minimul pentru conformerul cis si maximul pentru trans. Prin includerea unor termeni de acest fel pot fi descrise situatii oricat de complexe

In Figura II.4 este reprezentata pentru exemplificare simularea rotatiei in jurul legaturii HN - CO din amide:

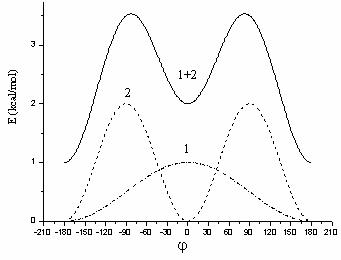
Figura II.4 Simularea rotatiei in jurul legaturii HN - CO:

1. n = 1 = 0; 2. n = 2 = 180; 1+2. rezultanta;

Aceasta simulare se realizeaza cu ajutorul a doua componente Fourier: una cu periodicitatea n = 1 si = 0 si cea de a doua cu n = 2 si = 180; marimea relativa a barierelor de potential indica o constanta de forta V₂ mai mare decat V₁.

Insumarea celor doua componente este deplasata in mod arbitrar cu 1 Kcal/mol. De remarcat ca rezultanta evidentiaza o stabilitate mai mare a formei trans (minimul pentru j = 180) decat cea a formei cis (minimul de la j = 0).

4 Energia datorata interactiilor intre atomii nelegati

Din categoria interactiilor intre atomi, separati la distante mai mari de doua legaturi chimice, fac parte cele datorate fortelor de tip van der Waals, legaturilor de hidrogen si fortelor de natura electrostatica.

1. Interactiile van der Waals

Aceste interactii sunt descrise de o functie 6 - 12, numita si functie Lennard-Jones:

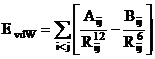(II.5)

R_ij este distanta intre cei doi atomi nelegati, iar A_ij si B_ij sunt parametrii van der Waals pentru perechea de atomi i si j.

Ecuatia (II.5) prezinta termeni atractivi R^-6 corespunzatorii interactiile de dispersie de tip London si termenii R^-12 corespunzatori interactiilor repulsive datorate principiului excluziunii al lui Pauli. Desi functia 6-12 este mai putin adecvate decat o functie exponentiala, este preferata datorita vitezei mai mari de calcul.

Dupa cum se observa din Figura II.5 atractia a doi atomi neutri aflati la o distanta mai mare de 4 Å este zero; interactia individuala van der Waals este in general mica minimul energetic fiind de cateva zecimi de Kcal/mol.

2. Interactia prin legaturi de hidrogen

Legatura de hidrogen nu este introdusa in mod explicit de toate campurile de forta deoarece, calculele cuantice evidentiaza ca legaturile de hidrogen pot fi puse in evidenta, in mod implicit, prin interactiile normale electrostatice.

Campul de forta AMBER foloseste un termen explicit pentru legaturile de hidrogen ca o recunoastere directa a importantei acestor legaturi pentru structura moleculara a biopolimerilor. Acest camp foloseste o functie 10 - 12 sugerata de Pauling:

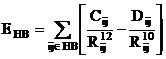        (II.6)

unde coeficientii C_ij si D_ij sunt parametrii termenilor repulsivi, respectiv atractivi, asociati perechilor donor-acceptor implicate in legaturi de hidrogen.

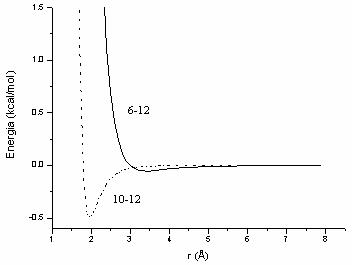
Figura II.5 Interactia van der Waals (6-12) si prin legaturi de hidrogen (10-12)

Functia (II.6) nu contribuie semnificativ la atractia celor doi atomi si este folosita in special pentru o mai fina reglare a distantei dintre acesti atomi. Dupa cum se constata din Figura II.5, pentru campul de forta AMBER, minimul functiei 10-12 corespunde la o energie in jur de 0,5 Kcal/mol pentru legatura de hidrogen.

3. Interactia electrostatica

Este redata de functia tipica, coulombiana, a interactiei a doua sarcini punctiforme si aflate la distanta R_ij:

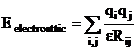(II.7)

Aceasta interactie este calculata numai pentru atomii nelegati; constanta dielectrica e utilizata in calcule este fie scalata prin utilizarea unui factor de scalare D , fie este considerata dependenta de distanta (Figura II.6).

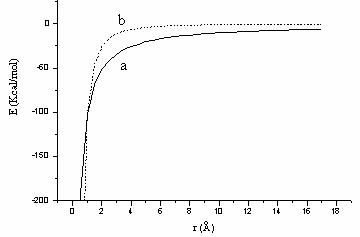
Figura II.6 Interactia electrostatica a doua sarcini punctiforme: +0,616

si -0,504:

a.     constanta dielectrica efectiva ; b. Constanta dielectrica

dependenta de distanta;

Atata timp cat moleculele de solvent nu sunt luate in mod explicit in calcul, mecanica moleculara cauta sa simuleze efectul de solvent prin modificarea constantei dielectrice fie printr-un factorul de scalare D, si in acest caz in relatia (II.7) e este inlocuit cu De, fie prin folosirea unei constante dielectrice dependenta de distanta, e fiind inlocuit cu eR_ij.

Factorul de scalare D poate lua valori intre 1.0 si 78.0 (valoare macroscopica a constantei dielectrice a apei) si are menirea sa atenueze interactiile electrostatice de lunga distanta.

Folosirea unei constante dielectrice dependente de distanta este justificata prin faptul ca simuleaza efectul de polarizare in interactiile atractive, prin ponderarea mai pronuntata a interactiilor la o distanta mai mica.

5 Aspecte suplimentare ale campului de forta

In afara termenilor generali prezentati in paragraful 4 mai pot fi intalniti in definirea campului de forta si alti termeni care au menirea fie sa imbunatateasca acuratetea modelarii moleculare, fie sa mareasca viteza de calcul.

1. Energia datorata modificarii unui unghi diedru impropriu

Acest termen are rolul sa mentina planeitatea unor atomi care se afla in acelasi plan, sau sa preintampine inversia atomilor de carbon tetraedrici cu un singur atom de hidrogen, in reprezentarea atomului unit (vezi mai departe). Utilizarea acestui termen conduce la o crestere a energiei in cazul deformarii unghiului diedru definit de un atom central si trei atomi invecinati.

Functia utilizata in acest caz este fie cea corespunzatoare ecuatiei (II.3) sau (II.4), sau o schema cu totul diferita ca cea utilizata de campul de forta MM+.

2. Termeni care presupun interactii vicinale 1 - 4

Desi interactiile vicinale 1 - 4 sunt tratate in mod normal ca interactii intre atomi nelegati, majoritatea campurilor de forta le trateaza in mod diferit de celelalte interactii intre atomi mai indepartati, prin folosirea unor factori de scalare subunitari; desi acesti factori de scalare sunt optionali nu este indicata modificarea lor intrucat valorile respective au fost folosite in timpul parametrizarii respectivului camp de forta.

Astfel factorii de scala folositi in HyperChem sunt dati in Tabelul :

Tabelul Factorii de scala pentru interactiile 1 - 4

3. Conceptul atomului unit

Datorita resurselor de calcul limitate, atat din punct de vedere al capacitatii cat si al vitezei, unele campuri de forta au introdus, spre simplificare, conceptul de atom unit ca tip de atom. Acest tip de atom trateaza anumite grupuri de atomi (atomi grei precum atomii de carbon si azot si atomii de hidrogen legati de acestia) ca un singur atom, cu parametrizari proprii care sa reflecte proprietatile atomilor constituenti.

Campurile de forta care folosesc conceptul atomului unit sunt folosite in special in cazul calculelor efectuate pentru biopolimeri, in scopul descresterii numarului de interactii intre atomii nelegati si implicit micsorarea timpului de calcul; totodata folosirea acestui gen de camp reduce dimensiunea suprafetii de energie potentiala.

Reprezentarea atomului unit este optionala pentru AMBER, este folosita automat pentru majoritatea atomi in OPLS si implicit pentru BIO+. Campul de forta MM+ nu foloseste aceasta reprezentare

4. Limitarea interactiilor atomilor nelegati

Calculele campului de forta privind interactiile atomilor nelegati sunt deseori trunchiate la o distanta finita in scopul salvarii resurselor de calcul. Aceasta procedura conduce de cele mai multe ori la o aproximatie destul de grosiera. De exemplu o simulare a dinamicii moleculare care apeleaza la o trunchiere abrupta a potentialului poate sa conduca la comportari anomale si fara semnificatii fizice. Unul dintre efecte este ca solutul se raceste in timp ce solventul se incalzeste rapid; apoi temperatura componentelor sistemului variaza lent pana cand sistemul ajunge intr-o stare aparenta, dar din pacate falsa, de echilibru.

O metoda relativ simpla pentru a preintampina acest neajuns al truncherii potentialului de interactie, este folosirea unei functii de intrerupere a potentialului. Folosirea unei astfel de functii permite o intrerupere lenta si sistematica a interactiilor incepand de la o anumita distanta, numita raza interioara, pana la o distanta limita numita raza externa, cand interactiile se anuleaza. In HyperChem aceste distante sunt 10 Å, respectiv 14 Å. Cu o functie de intrerupere adecvata, functia de potential nu va fi afectata decat in regiunea de intrerupere intre raza interioara si cea exterioara

O alta posibilitate este aceea a folosirii unui potential deplasat, prin inmultirea cu o functie de deplasare care se anuleaza cand distanta devine egala cu raza exterioara. Spre deosebire de functia de intrerupere, functia de deplasare va modifica potentialul pe intreg domeniul.

In folosirea acestor metode de limitare trebuie sa se tina seama de urmatoarele indicatii:

pentru molecule mici sau de marime medie nu se va folosi nici o metoda de limitare, deci se vor calcula toate interactiile;

pentru molecule mari (proteine, acizi nucleici) se va folosi functia de intrerupere care va micsora considerabil timpul de calcul;

functia de deplasare se va folosi numai in reproducerea unor rezultate experimentale; utilizarea ei nu este recomandata, tocmai datorita faptului ca intreaga suprafata de energie potentiala este afectata;

5. Folosirea constrangerilor

In anumite situatii pot fi fixate constrangeri in privinta valorilor pe care le au lungimile de legatura, distantele dintre atomi, unghiurile de valenta, unghiurile diedre, sau chiar pozitia in spatiu a atomilor.

Pentru a efectua o constrangere trebuie indicata valoarea respectiva si valoarea constantei de forta pentru potentialul respectiv.

Valorile recomandate pentru constantele de forta sunt:

pentru distantele interatomice: 7 Kcal/mol Ų;

pentru unghiul de valenta: 12,5 Kcal/mol Ų;

pentru un unghi diedru: 16,0 Kcal/mol Ų;

In situatia in care constrangerea nu este obtinuta se pot incerca constante de forta mai mari.