
|
|
|
Principiul de incertitudine
Succesul teoriilor stiintifice, in special al teoriei gravitatiei a lui Newton, a condus pe savantul francez marchizul de Laplace, la inceputul secolului al nouasprezecelea, sa considere ca universul era complet determinist. Laplace a sugerat ca ar trebui sa existe un set de legi stiintifice care ne-ar permite sa prezicem orice s-ar intampla in univers, numai daca am cunoaste starea completa a universului la un moment dat. De exemplu, daca stim pozitiile si vitezele soarelui si planetelor la un anumit moment, atunci putem utiliza legile lui Newton pentru a calcula starea Sistemului Solar in oricare alt moment. Determinismul pare destul de evident in acest caz, dar Laplace a mers si mai departe presupunand ca existau legi similare care guverneaza orice altceva, inclusiv comportamentul uman.
Doctrina determinismului stiintific a fost respinsa de multi oameni care simteau ca aceasta incalca libertatea lui Dumnezeu de a interveni asupra lumii, dar ea a ramas ipoteza clasica a stiintei pana in primii ani ai acestui secol. Una din primele indicatii ca aceasta ipoteza ar trebui abandonata a aparut atunci cand calculele savantilor britanici Lord Rayleigh si Sir James Jeans au sugerat ca un obiect fierbinte, sau un corp, cum ar fi o stea, trebuie sa radieze energie in cantitate infinita. Conform legilor in care credeam in acea vreme, un corp fierbinte trebuia sa emita unde electromagnetice (cum sunt undele radio, lumina vizibila sau razele X) in mod egal, la toate frecventele. De exemplu, un corp fierbinte ar trebui sa radieze aceeasi cantitate de energie in unde cu frecventele intre unu si doua milioane de milioane de unde pe secunda, ca si in unde cu frecvente intre doua si trei milioane de milioane de unde pe secunda. Dar, deoarece numarul de unde pe secunda este nelimitat, aceasta ar insemna ca energia totala radiata ar fi infinita.
Pentru a evita acest rezultat evident ridicol, savantul german Max Planck a sugerat, in 1900, ca lumina, razele X si alte unde nu pot fi emise intr-o cantitate arbitrara, ci numai in anumite pachete pe care le-a numit cuante. Mai mult, fiecare cuanta are o anumita cantitate de energie care este cu atat mai mare cu cat este mai mare frecventa undelor, astfel ca la o frecventa destul de inalta, emisia unei singure cuante ar cere mai multa energie decat era disponibila. Astfel, radiatia la frecvente inalte ar fi redusa, si deci cantitatea de energie radiata de corp ar fi finita.
Ipoteza cuantica a explicat foarte bine valoarea observata a emisiei radiatiei corpurilor fierbinti, dar implicatiile sale pentru determinism nu au fost intelese pana in 1926, cand un alt savant german, Werner Heisenberg, a formulat faimosul sau principiu de incertitudine. Pentru a prezice pozitia si viteza viitoare ale unei particule, trebuie sa i se poata masura precis pozitia si viteza actuale. Calea evidenta pentru a face acest lucru era sa se trimita lumina pe particula. Unele dintre undele de lumina vor fi imprastiate de particula si aceasta va indica pozitia sa. Totusi, pozitia particulei nu se va putea determina mai precis decat distanta dintre maximele undei de lumina, astfel ca pentru a masura precis pozitia particulei, este necesar sa se utilizeze lumina cu lungime de unda mica. Dar, conform ipotezei cuantice a lui Planck, nu se poate utiliza o cantitate arbitrar de mica de lumina ci trebuie sa se utilizeze cel putin o cuanta. Aceasta cuanta va perturba particula si-i va modifica viteza intr-un mod care nu poate fi prezis. Mai mult, cu cat se masoara mai precis pozitia, cu atat este mai scurta lungimea de unda a luminii necesare si deci cu atat este mai mare energia unei singure cuante. Astfel, viteza particulei va fi perturbata cu o cantitate mai mare. Cu alte cuvinte, cu cat incercati sa masurati mai precis pozitia particulei, cu atat mai putin precis si puteti masura viteza si viceversa. Heisenberg a aratat ca incertitudinea pozitiei particulei inmultita cu incertitudinea vitezei sale inmultita cu masa particulei nu poate fi niciodata mai mica decat o anumita cantitate numita constanta lui Planck. Mai mult, aceasta limita nu depinde de modul in care se incearca masurarea pozitiei sau vitezei particulei, sau de tipul particulei: principiul de incertitudine al lui Heisenberg este o proprietate fundamentala, inevitabila a lumii.
Principiul de incertitudine a avut implicatii profunde pentru modul in care vedem lumea. Chiar dupa mai mult de cincizeci de ani ele nu au fost complet intelese de multi filozofi si sunt inca subiectul multor controverse. Principiul de incertitudine a semnalat sfarsitul visului lui Laplace despre o teorie a stiintei, un model al universului care ar fi complet determinist: desigur, nu se pot prezice precis evenimente viitoare daca nu se poate masura precis starea actuala a universului! Ne putem inca imagina ca exista un set de legi care determina complet evenimentele pentru unele fiinte supranaturale, care ar putea observa starea actuala a universului fara sa o perturbe. Totusi, astfel de modele ale universului nu prea ne intereseaza pe noi, muritorii obisnuiti. Se pare ca este mai bine sa se utilizeze principiul economiei cunoscut drept briciul lui Occam, si sa se elimine toate aspectele teoriei care nu pot fi observate. Aceasta abordare i-a condus pe Heisenberg, Erwin Schrodinger si Paul Dirac in anii 1920 sa reformuleze mecanica intr-o noua teorie numita mecanica cuantica, bazata pe principiul de incertitudine. In aceasta teorie, particulele nu mai aveau viteze si pozitii separate, bine definite, care nu ar putea fi observate. In schimb, ele aveau o stare cuantica, care era o combinatie a pozitiei si vitezei.
In general, mecanica cuantica nu prezice un singur rezultat clar pentru o observatie. In schimb, ea prezice mai multe rezultate diferite posibile si ne spune cat de probabil este fiecare dintre ele. Aceasta inseamna ca, daca cineva face aceeasi masurare pe un numar mare de sisteme similare, fiecare incepand in acelasi fel, ar vedea ca rezultatul masurarii ar fi A intr-un anumit numar de cazuri, B in alt numar de cazuri s.a.m.d. S-ar putea prezice numarul corespunzator de ori in care rezultatul ar fi A sau B, dar nu s-ar putea prezice rezultatul specific al unei singure masurari. Prin urmare, mecanica cuantica introduce in stiinta. un element inevitabil de imprevizibilitate sau intamplare. Einstein a obiectat foarte puternic la aceasta, in ciuda rolului important pe care l-a jucat in dezvoltarea acestor idei. Einstein a primit premiul Nobel pentru contributia sa la teoria cuantica. Cu toate acestea, Einstein nu a acceptat niciodata ideea ca universul era guvernat de intamplare; sentimentele sale au fost exprimate in faimoasa sa afirmatie "Dumnezeu nu joaca zaruri". Totusi, majoritatea celorlalti savanti erau dispusi sa accepte mecanica cuantica deoarece era in perfecta concordanta cu experimentul. Intr-adevar, a fost o teorie remarcabil de reusita si ea sta la baza aproape a intregii stiinte si tehnologii moderne. Ea guverneaza comportarea tranzistorilor si circuitelor integrate care sunt componentele esentiale ale unor aparate electronice cum sunt televizoarele si computerele si reprezinta, de asemenea, baza chimiei si biologiei moderne. Singurele domenii din fizica in care mecanica cuantica nu a fost incorporata sunt gravitatia si structura la scara mare a universului.
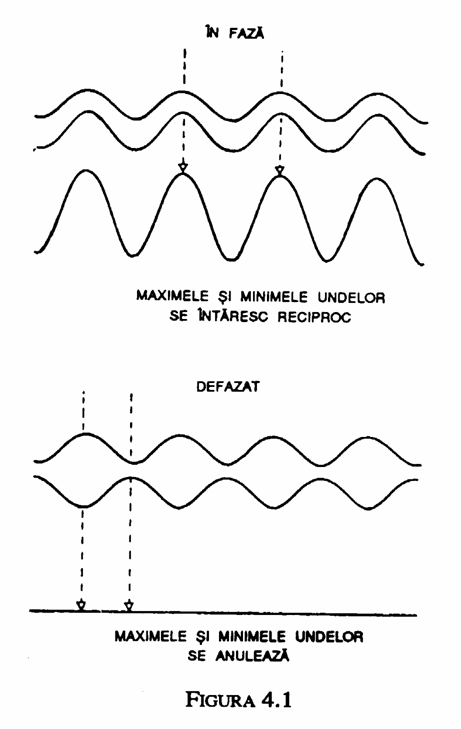
Desi lumina este formata din unde, ipoteza cuantica a lui Planck ne spune ca in unele cazuri ea se comporta ca si cand ar fi compusa din particule: ea poate fi emisa sau absorbita numai in pachete sau cuante. De asemenea, principiul de incertitudine al lui Heisenberg implica faptul ca particulele se comporta in anumite privinte ca niste unde: ele nu au o pozitie definita dar sunt "raspandite" cu o anumita probabilitate de distributie. Teoria mecanicii cuantice se bazeaza pe un tip de matematica complet nou, care nu mai descrie lumea reala in termeni de particule si unde; ea reprezinta numai observatii ale lumii care pot fi descrise prin acesti termeni. Exista astfel in mecanica cuantica un dualism intre unde si particule: pentru unele scopuri este util sa se considere particulele drept unde si pentru alte scopuri este mai bine sa se considere undele drept particule. O consecinta importanta a acestui fapt este ca se poate observa ceea ce se numeste interferenta dintre doua seturi de unde sau particule. Cu alte cuvinte, maximele unui set de unde pot coincide cu minimele celuilalt set. Atunci cele doua seturi de unde se anuleaza reciproc, in loc sa se adune intr-o unda mai puternica, asa cum ar fi de asteptat (fig. 4.1). Un exemplu familiar de interferenta in cazul luminii il reprezinta culorile care se vad adesea in baloanele de sapun. Acestea sunt cauzate de reflexia luminii pe cele doua fete ale peliculei subtiri de apa care formeaza balonul. Lumina alba consta din unde cu lungimi de unda diferite sau culori diferite. Pentru anumite lungimi de unda maximele undelor reflectate pe o parte a peliculei de sapun coincid cu minimele reflectate pe cealalta parte. Culorile care corespund acestor lungimi de unda lipsesc din lumina reflectata, care apare deci colorata.
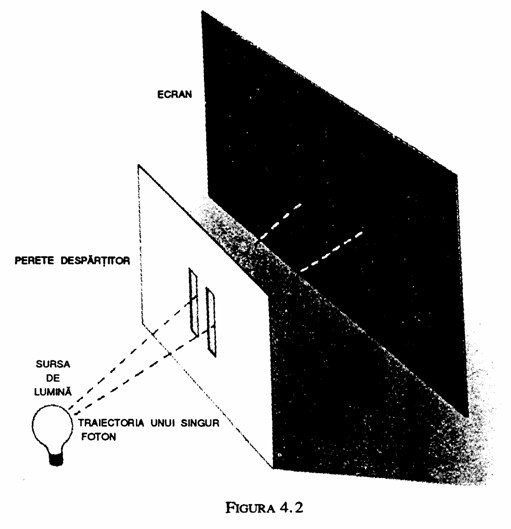
Interferenta se poate produce si pentru particule datorita dualismului introdus de mecanica cuantica. Un exemplu faimos este experimentul celor doua fante (fig. 4.2). Consideram un perete despartitor care are doua fante inguste taiate in el. Pe de o parte a peretelui se plaseaza o sursa de lumina cu o anumita culoare (adica, cu o anumita lungime de unda). Majoritatea luminii va lovi peretele, dar o cantitate mica va trece prin fante. Presupunem acum ca de partea cealalta a peretelui despartitor, cea opusa luminii, se plaseaza un ecran. Orice punct de pe ecran va primi unde de la cele doua fante. Totusi, in general, distanta pe care trebuie sa o parcurga lumina de la sursa la ecran prin cele doua fante va fi diferita. Aceasta va insemna ca undele care vin de la cele doua fante nu vor fi in faza atunci cand ajung la ecran: in unele locuri undele se vor anula reciproc si in altele se vor intari reciproc. Rezultatul este un model caracteristic de franje de lumina si intuneric.
Un lucru remarcabil este ca se obtine exact acelasi fel de franje daca se inlocuieste sursa de lumina cu o sursa de particule cum sunt electronii cu o viteza determinata (aceasta inseamna ca undele corespunzatoare au o lungime determinata). Acest lucru pare si mai ciudat pentru ca daca exista numai o fanta, pe ecran nu se obtin franje, ci doar o distributie uniforma de electroni. Se poate crede deci ca deschiderea unei alte fante ar mari numarul de electroni care lovesc fiecare punct de pe ecran, dar in realitate, in unele locuri din cauza interferentei numarul electronilor descreste. Daca electronii sunt trimisi prin fante unul cate unul, ar fi de asteptat ca fiecare sa treaca printr-o fanta sau alta si deci sa se comporte exact ca si cand fanta prin care trec ar fi singura acolo cand o distributie uniforma pe ecran. In realitate insa, chiar daca electronii sant trimisi unul cate unul, franjele tot apar. Prin urmare, fiecare electron trebuie sa: treaca prin ambele fante in acelasi timp!
Fenomenul de interferenta intre particule a fost crucial pentru intelegerea structurii atomilor, unitatile de baza in chimie si biologie si caramizile din care suntem facuti noi si tot ce este in jurul nostru. La inceputul acestui secol se credea ca atomii erau ca planetele care se deplaseaza pe orbite in jurul soarelui, cu electronii (particule de electricitate negativa) miscandu-se pe orbite in jurul unui nucleu central, care poseda electricitate pozitiva. Se presupunea ca atractia dintre electricitatea pozitiva si cea negativa tine electronii pe orbitele lor in acelasi fel in care atractia gravitationala dintre soare si planete tine planetele pe orbitele lor. Problema existenta aici era ca, inainte de mecanica cuantica, legile mecanicii si electricitatii preziceau ca electronii ar pierde energie si deci s-ar deplasa pe o spirala din ce in ce mai mica pana ce s-ar ciocni cu nucleul. Aceasta ar insemna ca atomul, si deci toata materia, trebuie sa sufere rapid un colaps catre o stare cu densitate foarte mare. O solutie partiala a acestei probleme a fost gasita de savantul danez Niels Bohr in 1913. El a sugerat ca poate electronii nu se pot deplasa pe orbite la orice distanta de nucleul central, ci numai la anumite distante specificate. Daca se mai presupune ca pe oricare din aceste orbite se pot misca numai unul sau doi electroni, aceasta ar rezolva problema colapsului atomului, deoarece electronii nu s-ar putea misca in spirala mai mult decat penŠu a umple orbitele cu distantele si energiile cele mai mici.
Acest model a explicat destul de bine structura celui mai simplu atom, hidrogenul, care are numai un singur electron ce se misca pe orbita in jurul nucleului. Dar nu era clar cum ar trebui sa fie extins la atomi mai complicati. In plus, ideea unui set limitat de orbite permise parea foarte arbitrara. Noua teorie a mecanicii cuantice a rezolvat aceasta dificultate. Ea a aratat ca un electron care se misca pe orbita in jurul nucleului poate fi considerat ca o unda, cu o lungime de unda care depinde de viteza sa. Pentru anumite orbite, lungimea orbitei ar corespunde unui numar intreg (in opozitie cu un numar fractionar) de lungimi de unda ale electronului. Pentru aceste orbite maximul undei ar fi in aceeasi pozitie de fiecare data cand si face o rotatie completa, astfel ca undele s-ar aduna: aceste orbite ar corespunde orbitelor permise ale lui Bohr. Totusi, pentru orbitele a caror lungime nu reprezinta un numar intreg de lungimi de unda, fiecare maxim al undei ar fi anulat in cele din urma de un minim atunci cand se face o rotatie; aceste orbite nu ar fi permise.
Un mod agreabil de vizualizare a dualismului unda/particula este asa-numita suma a istoriilor introdusa de savantul american Richard Feynman. In aceasta abordare se presupune ca particula nu are o singura istorie sau traiectorie in spatiu-timp asa cum ar fi intr-o teorie clasica, necuantica. In schimb, se presupune ca trece de la A la B prin fiecare traiectorie posibila. Fiecarei traiectorii ii sunt asociate doua numere: unul reprezinta dimensiunea undei si celalalt reprezinta pozitia in ciclu (adica, daca este un maxim sau un minim). Probabilitatea de trecere de la A la B se gaseste adunand undele pentru toate traiectoriile. In general, daca se compara un set de traiectorii invecinate, fazele sau pozitiile in ciclu vor diferi considerabil. Aceasta inseamna ca undele asociate acestor traiectorii se vor anula aproape exact una pe alta. Totusi, pentru unele seturi de traiectorii invecinate faza nu va varia mult de la o traiectorie la alta. Pentru aceste traiectorii undele nu se vor anula. Aceste traiectorii corespund orbitelor permise ale lui Bohr.
Cu aceste idei, in forma matematica concreta, a fost relativ simplu sa se calculeze orbitele permise in atomii mai complicati si chiar in molecule, care sunt formate din mai multi atomi mentinuti impreuna de electronii care se misca in jurul mai multor nuclee. Deoarece structura moleculelor si reactiile lor reciproce stau la baza chimiei si biologiei, mecanica cuantica ne permite, in principiu, sa prezicem aproape tot ce vedem in jurul nostru, in limitele determinate de principiul de incertitudine. (In practica, insa, calculele necesare pentru sisteme cu mai mult de cativa electroni sunt atat de complicate incat nu le putem efectua.)
Teoria generala a relativitatii a lui Einstein pare sa guverneze structura la scara mare a universului. Ea este ceea ce se numeste o teorie clasica; adica ea nu ia in considerare principiul de incertitudine din mecanica cuantica, asa cum ar trebui pentru a fi compatibila cu alte teorii. Aceasta nu conduce la discrepante cu observatia, deoarece toate campurile gravitationale pe care le simtim sunt foarte slabe. Totusi, teoremele singularitatilor discutate anterior arata ca exista cel putin doua situatii in care campul gravitational trebuie sa fie foarte puternic: gaurile negre si Big Bang-ul. In aceste campuri puternice, efectele mecanicii cuantice trebuie sa fie importante. Astfel, intr-un fel, relativitatea generalizata clasica, prezicand puncte cu densitate infinita, prezice propria sa disparitie, la fel cum mecanica clasica (adica necuantica) si-a prezis disparitia sugerand ca atomii trebuie sa sufere un colaps spre o densitate infinita. Nu avem inca o teorie completa, solida care sa unifice relativitatea generalizata si mecanica cuantica, dar cunoastem mai multe caracteristici pe care trebuie sa le aiba. Consecintele pe care acestea le-ar avea asupra gaurilor negre si Big Bang-ului vor fi descrise in capitolele urmatoare. Pentru moment, totusi, ne vom intoarce la incercarile recente de a reuni cunostintele noastre asupra celorlalte forte ale naturii intr-o singura teorie cuantica unificata.