
|
|
|
Experienta arata ca intre corpuri in stare de magnetizare, intre conductoare parcurse de curenti sau intre un conductor parcurs de curent si un corp magnetizat se exercita actiuni ponderomotoare (magnetice). Aceste actiuni se considera ca se realizeaza prin intermediul campului magnetic, deci existenta lor pune in evidenta implicit si prezenta campului magnetic. Se mai poate spune ca, corpurile magnetizate si conductoarele parcurse de curenti "produc" camp magnetic. In regim variabil, campul magnetic este produs si de un flux electric variabil in timp.
Din punct de vedere magnetic, exista
campuri statice, stationare si nestationare. Indiferent de
regim, campul inductiei magnetice este intotdeauna solenoidal (div ![]() = 0), adica liniile de camp corespunzatoare sunt
curbe inchise. In ceea ce priveste intensitatea campului magnetic,
= 0), adica liniile de camp corespunzatoare sunt
curbe inchise. In ceea ce priveste intensitatea campului magnetic, ![]() , aceasta are in cazul unor medii neomogene si o
componenta potentiala.
, aceasta are in cazul unor medii neomogene si o
componenta potentiala.
Caracterizarea campului magnetic intr-un
punct din vid se face cu ajutorul unei marimi vectoriale de stare,
numita inductia magnetica in vid, ![]() , (marime primitiva, definita pe baza de
efecte) cu unitatea de masura tesla [T] (1 T = 1 Wb/m2).
, (marime primitiva, definita pe baza de
efecte) cu unitatea de masura tesla [T] (1 T = 1 Wb/m2).
Experienta arata ca asupra unui mic corp incarcat cu sarcina electric si in miscare intr-un camp magnetic se exercita, in general, o forta. Aceasta forta, numita si forta magnetica sau forta Lorenz, este proportionala cu sarcina electrica, cu viteza corpului si este perpendiculara pe directia lui de miscare. Notand cu Q sarcina corpului de proba si cu v viteza corpului intr-un punct P din camp, expresia fortei este:
![]()
in care marimea vectoriala B (inductia magnetica in vid) depinde numai de pozitia punctului P si caracterizeaza campul magnetic in punctul respectiv.
Relatia (10.) se poate deci considera ca relatie de definitie a inductiei magnetice in vid. In aceasta relatie trebuie sa se tina seama si de semnul sarcinii electrice Q. forta maxima, Fmax, corespunde situatiei in care viteza corpului de proba este perpendiculara pe directia campului magnetic.
![]()
|
|
Din relatia (10.) se poate stabili ca directia vectorului inductie magnetica B, corespunde directiei de miscare a corpului de proba pentru care forta este nula. Notand cu a unghiul dintre vectorii v si B, valoarea fortei se poate scrie:
![]()
deci pentru a = 0 rezulta F = 0
Sensul inductiei magnetica s-a ales astfel incat la o sarcina pozitiva a corpului de proba, Q > 0, vectorii v, B si F sa formeze un sistem cartezian drept, respectiv sa fie asociati in aceasta ordine prin regula burghiului drept.
Daca in domeniul considerat pe langa campul magnetic considerat anterior, mai este prezent si un camp electric, asupra corpului de proba actioneaza forta rezultanta:
![]()
Aceasta expresie are un caracter mai general. Notand cu m masa si cu q0 sarcina electrica a unei particule elementare, ecuatia de miscare a acesteia intr-un camp electric si magnetic este:
![]()
Se observa ca forta
magnetica, fiind perpendiculara pe viteza v, nu are nici o
influenta asupra valorii acesteia. Inmultind relatia scalar
cu ![]() , se obtine expresia derivatei in raport cu timpul a
energiei cinetica a particulei
, se obtine expresia derivatei in raport cu timpul a
energiei cinetica a particulei
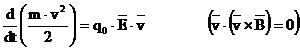
|
|

Din aceasta relatie
rezulta ca lucrul mecanic pe care-l efectueaza forta Fmag
asupra unei particule in miscare este nul. Variatia energiei cinetice
a unei particule in miscare situata atat intr-un camp electric cat
si intr-un camp magnetic se datoreaza deci numai fortei
corespunzatoare campului electric.
Ca si in cazul campului electric, se definesc si in camp magnetic liniile de camp ca fiind curbele astfel trasate incat in fiecare punct al lor vectorul inductie magnetica B ca fie tangent la ele. Ele pot fi vizualizate cu ajutorul piliturii de fier, aratand de exemplu ca in cazul unui fir conductor drept si suficient de lung, parcurs de curent, liniile de camp magnetic intr-un plan perpendicular pe fir sunt curbe inchise, circulare, cu centrul in axa firului.
|
|
Sensul inductiei magnetice se asociaza cu regula burghiului drept cu sensul curentului, adica inductia magnetica are sensul de rotire al burghiului drept pentru ca acesta sa inainteze in sensul curentului.
Pentru caracterizarea globala a proprietatilor campului magnetic se foloseste o marime scalara, numita flux magnetic, F. Acesta este o marime fizica derivata, definita pe baza relatiei:
![]()
in care ds este elementul de arie normal la suprafata S.
Legea fluxului magnetic este o lege generala, care se enunta astfel: fluxul magnetic printr-o suprafata inchisa S oarecare este intotdeauna nul, adica:
![]()
Din legea fluxului magnetic rezulta ca liniile campului magnetic sunt linii inchise (liniile lui B care intra in interiorul unei suprafete inchise trebuie sa si iasa prin acea suprafata pentru ca altfel integrala ar fi diferita de zero). Nu exista linii de camp magnetic care sa se termine sau sa porneasca din interiorul nici unei suprafete inchise.
In studiul campului magnetic se foloseste si o alta marime de stare vectoriala numita intensitatea campului magnetic, H. este o marime derivata ce se defineste in vid pe baza relatiei:
![]()
In care m0 este o constanta universala numita permeabilitatea vidului.
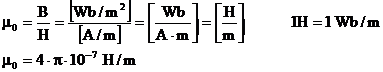
Experienta arata ca in regim stationar integrala de linie a intensitatii campului magnetic pe un contur inchis G (numita si tensiune magnetomotoare) este egala cu intensitatea curentului total ce strabate orice suprafata SG marginita de conturul G
![]()
Aceasta relatie este numita si teorema lui Ampere, fiind particularizarea pentru regim stationar a legii circuitului magnetic. Ea pune in evidenta faptul ca intensitatea campului magnetic reprezinta contributia exclusiva a curentilor electrici la producerea campului magnetic, nu si a corpurilor magnetizate.
|
|
Teorema lui Ampere permite calculul intensitatii campului magnetic in cazuri particulare si anume in medii omogene si pentru sisteme care prezinta o anumita simetrie.
![]() , cele doua marimi referitoare la campul magnetic
in vid fiind legate intre ele printr-o constanta, este evident faptul
ca starea campului magnetic in vid este de fapt caracterizata numai
printr-o singura marime de stare.
, cele doua marimi referitoare la campul magnetic
in vid fiind legate intre ele printr-o constanta, este evident faptul
ca starea campului magnetic in vid este de fapt caracterizata numai
printr-o singura marime de stare.
Relatia ![]() , stabilita in vid nu mai este adevarata in
puncte din interiorul corpurilor, fiind necesar sa se tina seama
si de magnetizarea acestora. In legatura cu starea de
magnetizare a corpurilor se disting doua cazuri. Daca starea de
magnetizare se manifesta numai in prezenta unui camp magnetic
exterior, se vorbeste de starea de magnetizare temporara, iar
daca starea de magnetizare este independenta de campul magnetic
exterior, ea se numeste stare de magnetizare permanenta. Corpurile cu
magnetizare temporara, spre deosebire de cele cu magnetizare
permanenta nu "produc" camp magnetic in mod autonom, ele insa
modifica campul magnetic in care sunt introduse.
, stabilita in vid nu mai este adevarata in
puncte din interiorul corpurilor, fiind necesar sa se tina seama
si de magnetizarea acestora. In legatura cu starea de
magnetizare a corpurilor se disting doua cazuri. Daca starea de
magnetizare se manifesta numai in prezenta unui camp magnetic
exterior, se vorbeste de starea de magnetizare temporara, iar
daca starea de magnetizare este independenta de campul magnetic
exterior, ea se numeste stare de magnetizare permanenta. Corpurile cu
magnetizare temporara, spre deosebire de cele cu magnetizare
permanenta nu "produc" camp magnetic in mod autonom, ele insa
modifica campul magnetic in care sunt introduse.
|
|
Starea de magnetizare a unui mic corp este
caracterizata printr-o marime vectoriala numita moment
magnetic, ![]() (marime
fizica primitiva). Asupra unui mic corp magnetizat situat in vid
intr-un camp magnetic exterior de inductie B, se exercita in general
un cuplu C si o forta rezultanta F avand expresiile:
(marime
fizica primitiva). Asupra unui mic corp magnetizat situat in vid
intr-un camp magnetic exterior de inductie B, se exercita in general
un cuplu C si o forta rezultanta F avand expresiile:
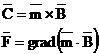
Daca campul magnetic este uniform se exercita numai cuplul C, iar daca campul este neuniform se exercita si o forta, F.
Ne vom referi la un mic corp cu magnetizare permanenta (de exp. un ac magnetic) situat in vid intr-un camp magnetic uniform. Corpul poseda o axa Dm, reprezentand directia de magnetizare a corpului, dupa care se considera orientat momentul magnetic m. sub actiunea cuplului care se exercita, corpul tinde sa se aseze astfel incat orientarea momentului magnetic sa coincida cu orientarea locala a inductiei magnetice.
Daca cuplul este maxim (a p/2), momentul magnetic rezulta din expresia:
![]()
In ceea ce priveste forta care es exercita asupra corpului, pentru componentele acesteia intr-un sistem de coordonate carteziene rezulta expresiile:
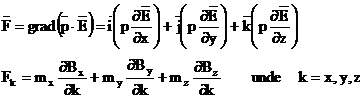
In cazul unor corpuri masive, pentru
caracterizarea starii locale de magnetizare se introduce o marime
vectoriala numita magnetizatie, ![]() . Notand cu
. Notand cu ![]() suma vectoriala a
momentelor magnetice dintr-un mic domeniu de volum Dv in jurul unui punct din corp,
magnetizatia este definita prin relatia:
suma vectoriala a
momentelor magnetice dintr-un mic domeniu de volum Dv in jurul unui punct din corp,
magnetizatia este definita prin relatia:
![]()
Magnetizatia reprezinta momentul magnetic al unitatii de volum.
Momentul magnetic total al unui corp se exprima in functie de magnetizatie prin relatia:
![]()
Experienta arata ca in cazul corpurilor cu magnetizatie temporara magnetizatia este dependenta de intensitatea campului magnetic. In forma generala, legea magnetizatiei temporare se poate scrie:
![]()
In cazul unor medii izotrope, ea se scrie sub forma:
![]()
este o lege de material
in care: ce este un parametru de material scalar adimensional, numit susceptivitate magnetica si depinde de punctul considerat din corp.
Daca
cm nu depinde de ![]() : medii liniare
: medii liniare
cm depinde de ![]() : medii neliniare
: medii neliniare
Experienta arata ca intr-un
punct dintr-un corp magnetizat, in prezenta campului magnetic, intre
marimile de stare ale campului (inductia magnetica ![]() si intensitatea campului magnetic
si intensitatea campului magnetic ![]() ) si marimea de stare a corpului (magnetizatia
) si marimea de stare a corpului (magnetizatia
![]() ) exista
urmatoarea relatie de legatura:
) exista
urmatoarea relatie de legatura:
![]()
care reprezinta o lege generala, valabila in orice regim al campului electromagnetic.
In
cazul corpurilor cu magnetizatie temporara: ![]()
![]()
unde:
![]() este o marime de
material, adimensionala, pozitiva, numita permeabilitate relativa
este o marime de
material, adimensionala, pozitiva, numita permeabilitate relativa
![]() este permeabilitatea
absoluta a materialului.
este permeabilitatea
absoluta a materialului.
mr caracterizeaza proprietatile magnetice ale materialelor. Cu cat mr este mai mare, cu atat materialul respectiv are proprietati magnetice mai bune.
In cazul campului electric, densitatea de energie electrica, adica energia din unitatea de volum, are expresia:
![]()
Energia electrica dintr-un volum oarecare v poate fi calculat cu relatia:
![]()
Densitatea de energia a campului magnetic are expresia:
![]()
respectiv energia magnetica dintr-un volum oarecare v este:
![]()
Fie cazul unei bobine cu miez magnetic
(presupunem un miez feromagnetic sub forma de tor pe care este
infasurata o bobina cu N spire parcurse de curentul I).
Energia magnetica poate fi exprimata in functie de curent
si fluxul magnetic din sectiunea torului. Scriind elementul de volum ![]() si considerand
ca fluxul este constant de-a lungul miezului (neglijand dispersia),
rezulta pentru energia magnetica expresia:
si considerand
ca fluxul este constant de-a lungul miezului (neglijand dispersia),
rezulta pentru energia magnetica expresia:
![]() dar:
dar: ![]() si
si ![]()
![]()
in care ![]() este fluxul magnetic
total = inlantuirea magnetica a bobinei
este fluxul magnetic
total = inlantuirea magnetica a bobinei
|
|
Considerand un element dl dintr-un circuit filiform parcurs de curentul i si situat intr-un camp magnetic exterior de inductie B, forta care se exercita asupra elementului de circuit are expresia:
![]() - forta lui
Laplace
- forta lui
Laplace
in care dl are orientarea intensitatii curentului electric.
(![]() )
)
Tinand seama de aceasta relatie, forta totala care se exercita in camp magnetic asupra unui conductor parcurs de curent si dispus dupa o curba oarecare C, este:
![]()
Daca se noteaza cu a unghiul pe care elementul dl il face cu inductia magnetica, pentru valoarea fortei elementare se obtine expresia.
dF = i dl B sina
Deci forta este nula daca a = 0 si este maxima pentru a p/2. Daca pentru o lungime l de conductor inductia magnetica este aceeasi si de asemenea este normala la directia conductorului, se obtine expresia simpla cunoscuta:
F = i l B (11.)
In ceea ce priveste orientarea fortei, se poate observa ca ea este perpendiculara pe planul constituit de elementul dl si inductia magnetica B.
|
|
Se considera cazul a doua circuite filiforme oarecare, coplanare, in vid, parcurse de curentii i1 si i2. Pentru calculul fortelor ce intervin se poate considera ca fiecare din cele doua circuite se gaseste in campul magnetic al celuilalt. Forta totala ce se exercita asupra conductorului 2:
![]()
![]() -
Biot-Savart-Laplace
-
Biot-Savart-Laplace
(pentru un cerc G ![]() )
)
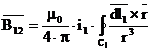
Expresia fortei devine: 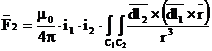
Iar valoarea fortei: ![]()
In conformitate cu principiul actiunii
si reactiunii, fortele care actioneaza asupra celor
doua circuite sunt egale: ![]() .
.
Relatia (12.) se poate scrie si sub forma:F = k i1 i2 in care constanta k depinde numai de configuratia si de pozitia relativa a celor doua circuite.
|
|
Un caz particular cunoscut se refera la doua conductoare filiforme, rectilinii si paralele de lungime teoretic infinita situate in aer la distanta d unul de celalalt. In aceste conditii, pentru forta care actioneaza asupra conductoarelor corespunzatoare unei lungimi l a acestora (F1 = F2 = F), rezulta expresia:
![]()
fiind forte de atractie daca curentii sunt de acelasi sens si forte de respingere pentru curenti de sens contrar.
(Sensul inductiei magnetice B2 se asociaza dupa regula burghiului drept curentului I2 iar elementului de linie dl1 are sensul lui I1, rezulta sensul lui dF1
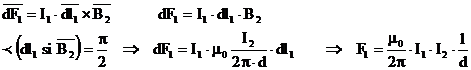 )
)
Forte de interactiune apar si in conductoare apartinand aceluiasi circuit. De exemplu intr-o spira parcursa de curent, aceste forte tind sa mareasca suprafata spirei.