Motor de curent continuu - Teste pentru verificarea performantelor

Schema echivalenta pentru teste este:

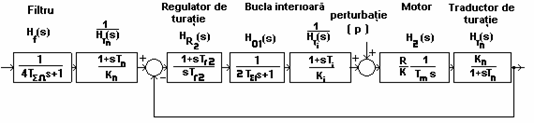
Figura 6.1 - schema echivalenta a SRA fara filtrare si fara perturbatie

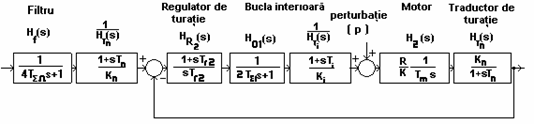
Figura 6.2 - schema echivalenta a SRA cu filtrare si cu perturbatie

Functia de transfer a sistemului de reglare supus unei marimi de intrare R(s) de tip treapta fara perturbatie si fara filtrare este urmatoarea:

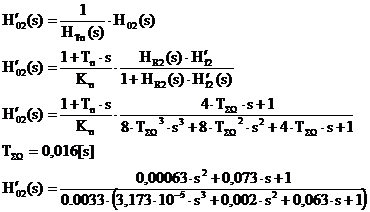
Functia de transfer a sistemului de reglare supus unei marimi de intrare de tip treapta, fara perturbatie cu filtrare este:

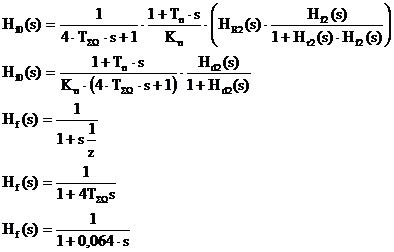
Unde:        - H_d2 - functia de transfer a intregului sistem pe calea directa;

H'₀₂ - functia de transfer a intregului sistem inchis, respectiv al SRA al turatiei.

In aceasta functie se evidentiaza doi poli dominanti si in plus o pereche de poli-zero evidentiati prin p si z.

Functia de transfer a sistemului de reglare dupa perturbatie:

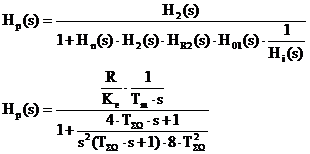
Valoarea exacta se calculeaza in MATLAB:

Teste de regim stationar:

Pentru o intrare de tip treapta unitara:

R(s 1/s

eroarea stationara este:

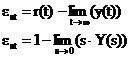
iesirea sistemului:

Y(s H₀(s)·R(s)

deci

Y(s H₀(s)·(1/s)

e_st 0    pentru intrarea tip treapta unitara

Pentru perturbatii de forma: P(s 1/s:

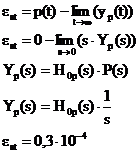
Pentru o intrare: R(s)=1/s², eroarea stationara este:

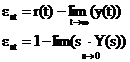
in care:

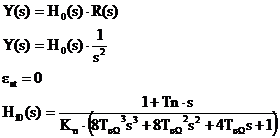
Asupra acestor sisteme se vor aplica urmatoarele teste folosind programul MATLAB, verificand si deducand urmatoarele:

1.     pentru sistemul inchis un semnal treapta nefiltrat conduce la un suprareglaj s=45[%] si durata regimului tranzitoriu t_t=0,4[s];

2.     pentru sistemul inchis o intrare treapta conduce la s = 8[%] si durata regimului tranzitoriu t_t=0,25[s];

3.     raspunsul sistemului pentru intrare de tip rampa. Acest test se va aplica functiei H_02f(s);

4.     raspunsul sistemului la o perturbatie de tip treapta. Acest test se va aplica functiei Hp(s).