
|
|
|
FILTRE CU RASPUNS FINIT LA IMPULS
In acesta lucrare este studiat un Filtru Trece Jos Real, caracterizat de diferite ordine si frecvente, prin comparatie cu unul ideal.
Fie sistemul :
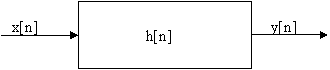 |
Acesta este caracterizat de functia raspuns la impuls h[n] care se obtine daca la intrarea sistemului se aplica impulsul Dirac discret. d[n] Dupa aceasta functie filtrele se impart in FIR(filtre cu raspuns finit la impuls) si RII(filtre cu raspuns infinit la impuls).
Transormata Fourier a functiei raspuns la impuls se numeste raspuns in frecventa.
|
Conditia suficienta si necesara ca sistemul sa fie stabil este :
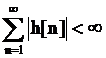 |
FTJ studiat este liniar si invariant in timp.
Pentru diferite frecvente f2, minime si ordine se compara prin intermediul erorii patratice FTJ real cu cel ideal.
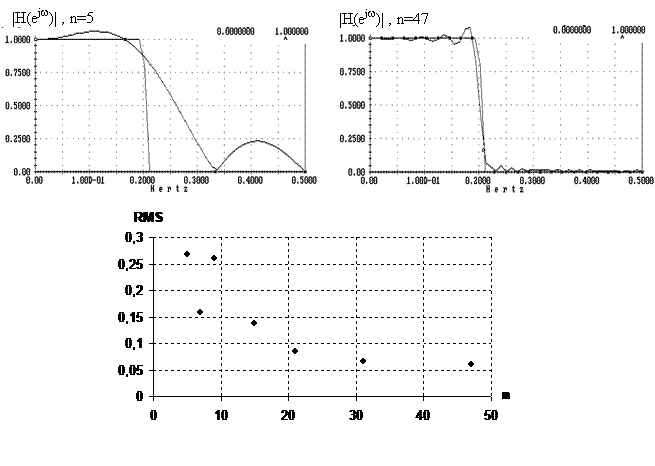
1) f1=0,2 f2=0,21 Max=1 Min=0,001
n
5
7
9
15
21
31
47
RMS
0,2685
0,1592
0,2610
0,1383
0,0841
0,0659
0,0607
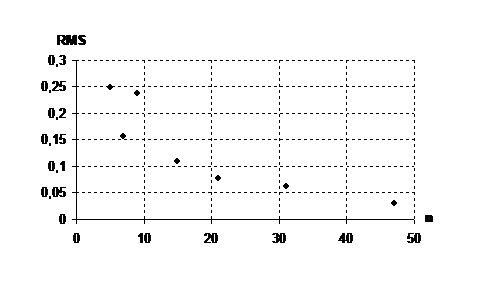
2) f1=0,2 f2=0,22 Max=1 Min=0,001
 n
n
5
7
9
15
21
31
47
RMS
0,2497
0,157
0,2372
0,109
0,077
0,0621
0,031
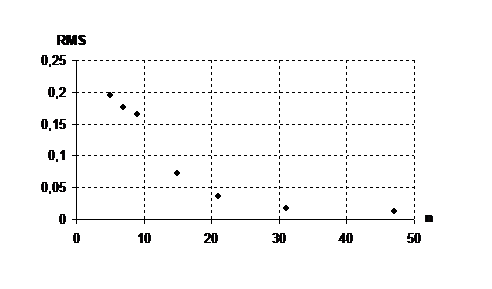
3) f1=0,2 f2=0,25 Max=1 Min=0,001
 n
n
5
7
9
15
21
31
47
RMS
0,1943
0,1764
0,1654
0,0717
0,0357
0,0178
0,0127
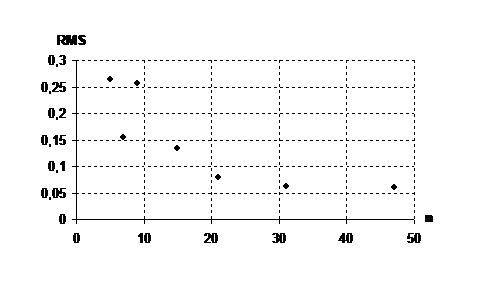
4) f1=0,2 f2=0,21 Max=1 Min=0,01
n
5
7
9
15
21
31
47
 RMS
RMS
0,2637
0,1538
0,2569
0,1345
0,0801
0,0624
0,0596
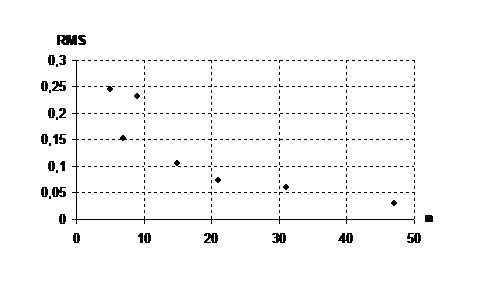
5) f1=0,2 f2=0,22 Max=1 Min=0,01
 n
n
5
7
9
15
21
31
47
RMS
0,2449
0,1525
0,2330
0,1056
0,0728
0,0595
0,0306
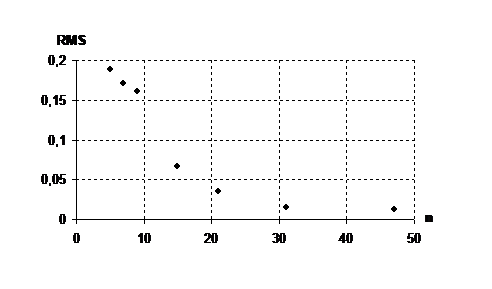
6) f1=0,2 f2=0,25 Max=1 Min=0,01
n
5
7
9
15
21
31
47
 RMS
RMS
0,1891
0,1713
0,1610
0,0661
0,0352
0,0155
0,0120