Ecuatile statice de functonare pentru regim de functonare stabil

ECUATILE STATICE DE FUNCTONARE PENTRU REGIM DE FUNCTONARE STABIL

A.       Comanda in functie de timp

1). Durata activa 0 < t < dT

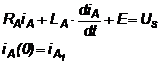(3.4.a)

solutia este:

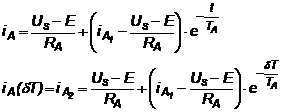(3.4.b)

2). Durata de pauza dT < t < T

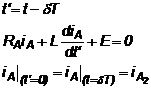(3.5.a)

solutia este:

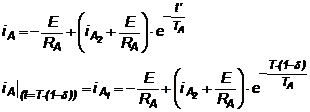(3.5.b)

Prin rezolvarea sistemului de ecuatii format din relatiile 3.4 si 3.5 se obtine:

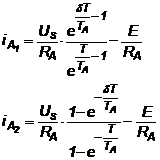(3.6)

Definim ondulatia de curent prin relatia:

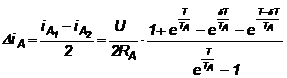(3.7.a)

si are valoarea maxima pentru d = 0,5

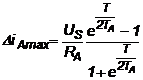(3.7.b)

Dezvoltarea in serie Fourier a curentului I_A conduce la amplitudinea fundamentalei curentului:

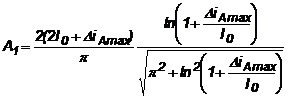(3.8)

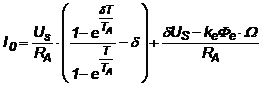(3.9)

Situatia cea mai defavorabila corespunde la limita curentului intrerupt, adica pentru I₀ = I_min = 0. Limitand valoarea eficace a fundamentalei la o valoare impusa k_wI_An rezulta prin dezvoltare in serie de puteri a exponentialei care apare in expresia analizata si neglijand termenii de grad superior (T << 2T_A

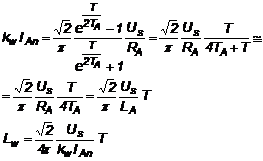(3.10)

unde L_w este valoarea necesara a inductantei de netezire (filtrare) folosita. Se remarca dependenta acestei valori de perioda de lucru.

Observatii

F           In regim stabilizat de functionare, valoarea medie a caderii de tensiune pe bobina este zero. Astfel:

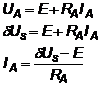(3.11)

F           Daca fluxul de excitatie este constant, atunci in regim stabilizat de functionare, cuplul de sarcina M_S este egal cu cuplul electromagnetic M si este proportional cu valoarea curentului din indusul masinii de curent continuu, I_A. Astfel rezulta:

(3.12.a)

F           Pentru o variatie lineara (panta curentului indus, constanta) a curentului I_A atat pe durata cand chopperul este activ, cat si pe durata de pauza, avem:

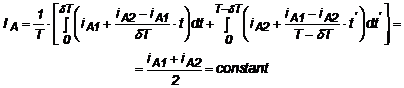
(3.12.b)

O astfel de valoare a curentului mediu prin indusul masinii de curent continuu poate duce la aparitia fenomenului de instabilitate statica de functionare, deoarece pentru aproximatia considerata anterior nu a contat caracterul sarcinii masinii.

B.       Comanda in functie de curent

Analizand ecuatiile 3.4 si 3.5 se obtine:

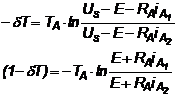(3.13-3.14)

Din ecuatiile 3.13-3.14 rezulta perioada T si din ecuatia 3.13 se obtine coeficientul d . Astfel, rezulta valoarea medie a curentului prin indusul masinii, respectiv valoarea cuplului electromagnetic dezvoltat de catre aceasta:

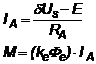(3.15)

Observatie

F           Daca intervalele dT si (1-dT) sunt mult mai mici decat T_A, iar variatia de la i_A1 la i_A2 si invers se considera practic constanta, atunci se obtine o instabilitate pentru marea majoritate a sarcinilor:

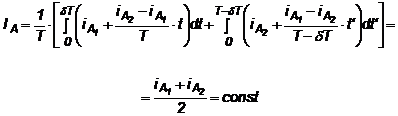
(3.16)