|
|
|
Analiza armonica a semnalelor
Scopul lucrarii: Prezentarea conceptelor de serie Fourier complexa (SFC) si serie Fourier reala (SFR). Semnificatia fizica a SFR. Folosirea milivoltmetrului selectiv pentru masurarea spectrelor unor semnale periodice remarcabile. Masurarea factorului de distorsiuni armonice.
Rezumat teoretic:
Reprezentarea vectoriala a unui semnal se bazeaza pe dezvoltarea acestuia intr-o combinatie liniara de functii φk(t), k=1,2,n:
1
unde n este dimensiunea spatiului vectorial (eventual n= ), iar setul de functii φk(t) formeaza o baza a spatiului vectorial respectiv. Cei n coeficienti αk constituie o reprezentare discreta a semnalului x(t) si formeaza ceea ce se numeste spectrul semnalului x(t) relativ la setul de functii φk(t).
In
orice spatiu vectorial se defineste produsul scalar a doi vectori x
si y, notat cu <x,y> si pe baza acestuia norma unui vector 
2. Baza spatiului
vectorial se numeste ortogonala daca
<φk,φm>=0, k,m, k m. Baza
se numeste ortonormata daca in plus mai
este satisfacuta conditia φk =1, k.
Un exemplu de baza ortonormata pe spatiul vectorial L2(T) il constituie setul de functii periodice de perioada T de tip exponentiala complexa:
3
unde 
4=Ω, pulsatia
semnalului periodic de perioada T. Se poate arata ca <φk(t),φm(t)>=0
si ca φk(t) =1, cu
produsul scalar definit in L2(T):
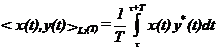
5
si cu norma indusa de acesta.
Seria Fourier complexa. Un semnal periodic de perioada T, fT(t), se poate descompune in serie Fourier complexa conform relatiei:
6
Coeficientii ck formeaza spectrul semnalului fT(t) in raport cu setul de functii φk(t) si se calculeaza cu relatia:
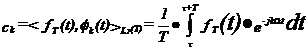
7
τ oarecare. Integrala din relatia de mai sus se face pe o singura perioada a semnalului periodic, deci se mai poate scrie:
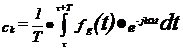
8
unde cu fg(t) s-a notat pulsul generator al semnalului periodic fT(t), adica o functie de tipul:
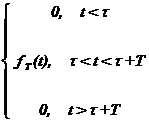
9
fg(t)=
Observatie: Semnalul fg(t) definit astfel nu este unic. Exista o infinitate de semnale absolut integrabile care prin periodizare cu perioada T dau un acelasi semnal periodic fT(t).
Semnalul fg(t) este un semnal cu suport finit in timp, deci admite transformata Fourier Fg(ω)=_ definita prin relatia:
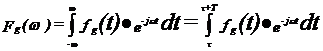
10
Comparandu-se ultimele doua relatii se observa ca:
11
1 Fig. 1
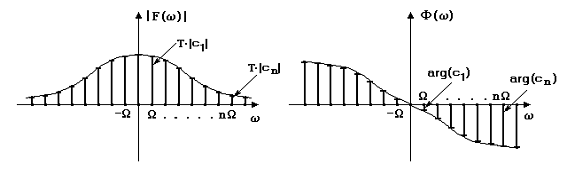
Coeficientii ck sunt marimi complexe:
12
O interpretare intuitiva a semnificatiei coeficientilor ck este data in figura 1 unde se observa ca T.ck reprezinta modulul lui Fg(ω) in punctele kΩ, iar arg(ck)=argFg(ω)ω=kΩ.
Seria Fourier reala. Plecand
de la seria Fourier complexa si observand ca pentru un semnal fg(t)
real 
13, rezulta ca 
14, deci SFC se poate
rescrie astfel:
15
Ultima relatie obtinuta constituie o forma de scriere a seriei Fourier reale. O alta forma a seriei Fourier reale o constituie descompunerea semnalului periodic fT(t) in armonici de sinusuri si cosinusuri:
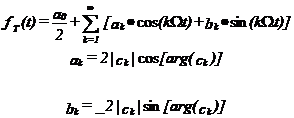
16
Coeficientii ak si bk se pot calcula si cu relatiile:
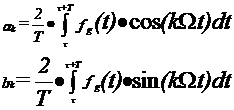
17
In particular, limitele de integrare in
relatiile de mai sus pot fi 
18 si 
19. In aceasta
situatie, pentru o functie para fg(t)=fg(-t)
rezulta ca bk=0, k, iar pentru o functie impara
fg(t)=-fg(-t) toti coeficientii ak=0,
inclusiv pentru k=0.
Semnificatia fizica a SFR. Vom considera cazul semnalului periodic dreptunghiular, reprezentat in figura 2. Ca puls generator al acestui semnal periodic vom considera semnalul reprezentat in figura 3.
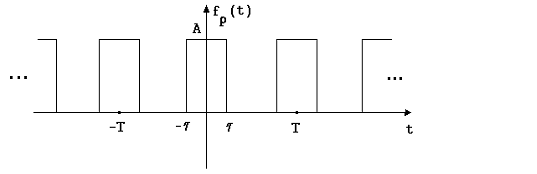
2 Fig. 2
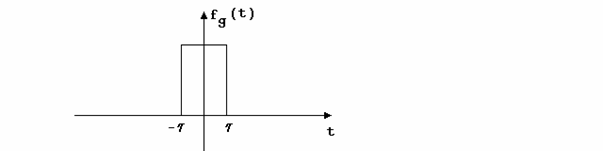
3 Fig. 3
Transformata Fourier a lui fg(t) este:
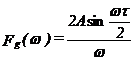
20
Deoarece fg(t) am ales-o functie para a rezultat Fg(ω) reala, deci si toti coeficientii ck sunt reali, fiind dati de relatia:
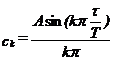
21
Componenta
continua a lui fT(t) este :
22
Vom particulariza semnalul periodic dreptunghiular
considerand τ=
23 si anuland
componenta continua. In aceasta situatie coeficientii ck
vor fi dati de relatia:
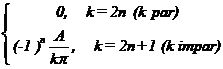24
ck=
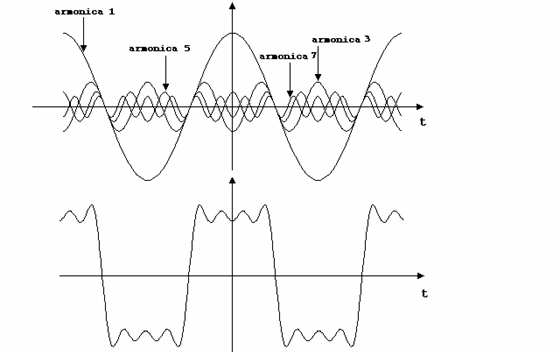
Semnificatia fizica a SFR este aceea ca un semnal periodic poate fi vazut ca o suma (finita sau infinita) de sinusuri si cosinusuri (sau numai de cosinusuri, dar cu diferite faze initiale), asa cum se arata in figura 4 pentru semnalul periodic dreptunghiular alternativ cu factor de umplere ½. In figura 4 au fost reprezentate numai primele 4 armonici impare (o data separate si apoi sumate), dar se observa ca suma acestora se apropie de-acum de forma semnalului dreptunghiular periodic.
4 Fig. 4
Ca o dovada ca aceste armonici exista fizic, ele pot fi masurate cu ajutorul milivoltmetrului selectiv acordandu-l succesiv pe frecventa semnalului periodic dreptunghiular si pe multiplii intregi ai acesteia.
Se observa de asemenea ca pentru semnalul periodic dreptunghiular alternativ cu factor de umplere ½ este satisfacuta relatia:
25
deci amplitudinea armonicilor scade odata cu cresterea ordinului lor, k.
Analiza armonica a unor semnale periodice remarcabile.
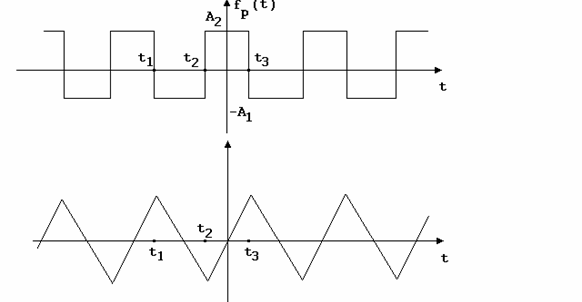
1.Semnalul periodic triunghiular. Forma in timp a acestui semnal este reprezentata in figura 5. Semnalul periodic triunghiular poate fi obtinut prin integrarea semnalului periodic dreptunghiular cu componenta continua nula, altfel prin integrare semnalul rezultat ar tinde catre ± , in functie de semnul componentei continue a semnalului dreptunghiular. Pe perioada (t1, t2), cand semnalul dreptunghiular este negativ si de amplitudine -A1, prin integrare se obtine un semnal descris de relatia -A1.t, iar in perioada (t2, t3), cand semnalul dreptunghiular are amplitudinea A2 pozitiva, prin integrare se obtine A2.t, s.a.m.d.
5 Fig. 5
Tinand cont de acest lucru si bazandu-ne pe urmatoarea proprietate a transformatei Fourier:
daca
26 atunci 
27
rezulta ca spectrul semnalului periodic triunghiular este dat de:
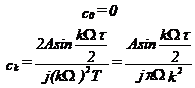
28
unde A=A1+A2.
Pentru cazul particular in care se pleaca de la semnal periodic dreptunghiular cu factor de umplere ½ se obtine:
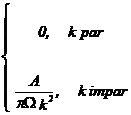
29
ck=
Se observa ca amplitudinile armonicilor impare, ck, scad cu k2.
2.Semnal periodic format din impulsuri Dirac alternative. Acest semnal se obtine prin derivarea semnalului periodic dreptunghiular si are forma reprezentata in figura 6. Amplitudinea impulsurilor Dirac este egala cu amplitudinea A a saltului din cadrul semnalului dreptunghiular.
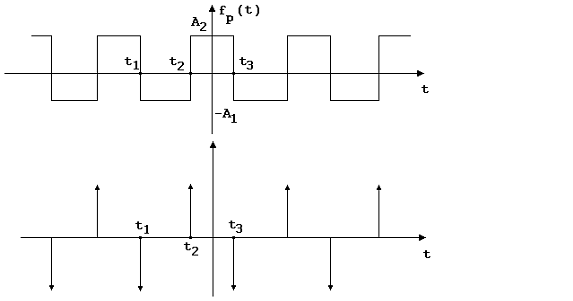
6 Fig. 6
Bazandu-ne acum pe urmatoarea proprietate a transformatei Fourier:
daca
30 atunci 
31
rezulta ca:
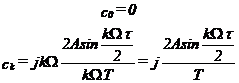
32
iar pentru cazul particular al factorului de umplere ½ rezulta:
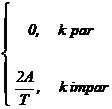
33
ck=
Se observa ca amplitudinile armonicilor impare sunt constante, indiferent de ordinul k al armonicii.
Coeficientul de distorsiuni armonice. De multe ori ne intereseaza cit de mult difera un semnal periodic nesinusoidal de semnalul periodic sinusoidal pur. O astfel de situatie se intalneste de exemplu la testarea amplificatoarelor cand se doreste sa se determine in ce masura amplificatorul respectiv distorsioneaza (modifica) forma unui semnal periodic sinusoidal aplicat la intrare, distorsiuni datorate neliniaritatilor inerente existente in circuit. Ca o masura a acestor distorsiuni s-a introdus marimea numita coeficient de distorsiuni armonice δ, definita astfel:
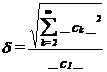
34
Modul de lucru:
1. Se genereaza un semnal dreptunghiular periodic folosind generatorul de joasa frecventa si se vizualizeaza forma acestui semnal in timp pe ecranul osciloscopului. Se masoara frecventa si amplitudinea semnalului dreptunghiular periodic. Se calculeaza pe baza acestor masuratori valorile modulurilor coeficientilor ck. Ce semnificatie fizica au aceste valori?
2. Se aplica semnalul periodic dreptunghiular si la intrarea milivoltmetrului selectiv. Stiind ca acest aparat indica valorile efective ale componentelor armonice ale semnalului aplicat la intrare determinati pe baza calculelor anterioare ce indicatii ar trebui sa va dea milivoltmetrul selectiv. Atentie! Daca valoarea efectiva corespunzatoare primei armonici a rezultat mai mare de 1V micsorati nivelul semnalului dreptunghiular la o astfel de valoare incit valoarea efectiva a primei armonici sa fie mai mica de 1V (aceasta reprezinta valoarea maxima ce poate fi masurata cu milivoltmetrul selectiv) si reluati masuratorile de la punctul 1.
3.
Masurati cu milivoltmetrul selectiv nivelul armonicilor semnalului
dreptunghiular periodic si comparati aceste valori cu cele calculate.
Respecta valorile masurate relatia 
35 pentru k impar? Daca
nu explicati de ce. Completati urmatorul tabel:
k=1
k=2
k=3
k=4
k=5
k=6
k=7
ck
Valori efective calculate
Valori efective masurate
4.
Realizati un circuit integrator si obtineti plecand de la
semnalul dreptunghiular periodic un semnal triunghiular periodic.
Masurati cu milivoltmetrul selectiv spectrul acestui semnal. Respecta
valorile masurate relatia 
36 pentru k impar?
5. Realizati un circuit derivator si obtineti plecand de la semnalul periodic dreptunghiular un semnal periodic alternativ format din impulsuri foarte inguste. Masurati cu milivoltmetrul selectiv spectrul acestui semnal. Se respecta faptul ca toate liniile spectrale sunt egale? Explicati de ce nu se respecta acest lucru. Completati tabelul de mai jos:
k=1
k=2
k=3
k=4
k=5
k=6
k=7
Semnal triunghiular
Semnal cu impulsuri
6. Aplicati de la generatorul de joasa frecventa la intrarea milivoltmetrului selectiv un semnal periodic sinusoidal cu amplitudine mai mica de 1,41V. Masurati spectrul acestui semnal si calculati indicele de distorsiuni armonice luand in considerare numai primele 7 armonici.
Intrebari suplimentare:
1. Se aplica la intrarea unui circuit liniar caracterizat de functia de transfer H(s) un semnal periodic de perioada T. Cum este semnalul de la iesirea circuitului? Ramane el periodic sau nu, iar daca ramane care este perioada sa?
2. Daca semnalul periodic de mai sus are spectrul , care este spectrul semnalului de la iesirea circuitului liniar H(s)?
3. Liniile spectrale ale semnalului de la iesirea unui circuit liniar excitat cu un semnal periodic sunt in raport cu liniile spectrale ale semnalului de la intrare:
a) mai multe ca numar;
b) mai multe sau acelasi numar;
c) strict acelasi numar;
d) mai putine sau acelasi numar;
e) mai putine.
4.
Fie 
37, unde P(jω0 0 si
e(t)=A+Bcosω0t. Semnalul e(t) este periodic sau nu? Care este
spectrul sau? Cate linii spectrale are acest spectru? Care este spectrul
semnalului de la iesirea circuitului caracterizat de H(s)? Cate linii
spectrale contine?
5. Dati exemplu de un semnal neperiodic dar care are un spectru discret.
