
|
|
|
DIAGRAME DE EFORTURI PENTRU BARE DREPTE
Etape de calcul IN SASE PASI
1. Calculul reactiunilor (sistemelor static determinate)
- Fixarea originii si a sistemului de axe;
- Delimitarea intervalelor cu notarea sectiunilor:
* schimbare incarcare
* variatia dimensionala a sectiunii
* articulatii
- Inlocuirea reazemelor cu reactiuni.
denumire
simbolizare
prin
redesemnare
prin
suprapunere
Articulatie mobila
(simpla rezemare)
![]()
![]()
![]()
Articulatie fixa
![]()
![]()
Incastrare
![]()
![]()
Scrierea ecuatiilor de echilibru static, rezolvarea lor cu determinarea reactiunilor(Σ X) = 0; (ΣY) = 0; (Σ M) = 0;
Observatie. Pentru calculul reactiunilor sarcinile distribuite se inlocuiesc cu sarcini concentrate echivalente.
- Indicarea valorilor reactiunilor pe desen (fixarea sensului real al reactiunilor)
- Verificarea reactiunilor.
2. Efectuarea de sectiuni oarecare pe fiecare tronson de schimbare de incarcare. De fiecare tronson este legat un sistem de axe cartezian xOy cu originea in inceputul tronsonului si cu xmax la capatul tronsonului. In cazul in care avem tronsoane se recomanda (pentru simplificarea calculelor) intoarcerea sensului de crestere a axei Ox pentru tronsoanele ce depasesc numarul n/2.
3. Scrierea expresiilor functiilor de eforturi sectionale N, T si Mi pe fiecare interval (pe desen ), ca suma algebrica a tuturor sarcinilor (inclusiv reactiunile) care se gasesc in stanga (sau dreapta) sectiunii considerate:
Nx Σ Ni , Ty = Σ Ti, Miz = Σ Mi
Observatie. Regula de semne pentru eforturi sectionale:
Semn
T
Mi
Pozitiv
![]()
![]()
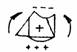
Negativ
![]()
![]()
![]()
4. Determinarea valorilor functiilor de eforturi pentru capetele de interval prin inlocuirea valorilor x = 0 si x xmax si scrierea lor in pozitia lor din desen.
Observatie. In cazul in care functia forta taietoare pe un interval ia valori la capete de interval de semne contrare exista o sectiune in interval in care functia se anuleaza. In acest caz se egaleaza functia cu zero si se calculeaza pozitia acestei sectiuni (notata ξ).
Valoarea lui ξ anterior calculata se inlocuieste in functia moment incovoietor a intervalului respectiv pentru a se determina minimul sau maximul valorii efective a momentului incovoietor.
5. Trasarea diagramelor de eforturi pe baza valorilor (cu semnele lor) calculate la capete de interval si a tipului de functie (liniara, parabolica, etc).
Observatie. Reguli de reprezentare:
Semn
T
Mi
Pozitiv
![]()
![]()
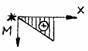
Atentie, Mi pozitiv are sensul in jos reprezentand diagrama de momente incovoietoare pe fibra intinsa.
6. Verificarea diagramelor de eforturi. Reguli:
a). Pentru T
- Pe intervalul dintre sarcini concentrate (daca p = 0) T = constant.
- In dreptul sarcinilor concentrate diagrama T are un salt (discontinuitate)
egal cu valoarea fortei.
b). Pentru Mi
- Pe intervalul dintre sarcini concentrate (daca p = 0) Mi variaza liniar
- In dreptul momentului concentrat diagrama Mi are un salt egal cu
valoarea momentului concentrat
- Mi in articulatie cu reazeme extreme (daca nu exista Mi) este nul.
Verificare corelativa :
T = 0; Mi = constant
T = 0; pentru un x , Mi = valoare extrema
T > 0 T Mi creste
T < 0 T Mi scade.