Analiza energetica a grupurilor cogenerative binare de transport

ANALIZA ENERGETICA A GRUPURILOR COGENERATIVE BINARE DE TRANSPORT

1. Notiuni introductive

Asa cum s-a precizat in capitolul 1, prezenta CRGA, a condensatorului turbinei cu abur si, eventual, a recuperatorului TMG, constituie dezavantajul major al utilizarii grupurilor binare ca sisteme de propulsie terestra. Aceste componente impun un spor de greutate si volum, care poate altera dinamica si gabaritul vehiculului respectiv.

Dimensiunile optime ale recuperatorului TMG, CRGA si condensatorului sunt cele care permit obtinerea unor avantaje economice maxime (economie maxima de combustibil) cu un spor de greutate si volum minim. Solutionarea acestei probleme impune realizarea unor programe de calcul care sa aiba in vedere urmatoarele obiective:

Stabilirea parametrilor termodinamici in punctele importante ale celor doua cicluri (cu gaze si cu abur) la diferite regimuri si pentru diferite scheme termodinamice de grupuri binare;

Estimarea performantelor ciclului cu gaze, ale ciclului cu abur si ale ciclului combinat pentru diferitele scheme termodinamice de grupuri binare in scopul determinarii acelor scheme care sunt optime din punct de vedere al performantelor;

Calculul si optimizarea suprafetei recuperatorului TMG, a celor trei suprafete de schimb de caldura (supraincalzitor, vaporizator, economizor) ale CRGA si a suprafetei condensatorului.

3.2. Scheme termodinamice analizate

In cazul grupurilor binare conventionale, pierderile de apa apar, in marea lor majoritate, in instalatia de condensare si se datoreaza turnului de racire. Prin urmare, reducerea pierderilor de apa ale grupurilor binare presupune utilizarea unor sisteme de condensare care sa functioneze cu un consum redus de apa. Solutia adoptata in studiile efectuate are la baza schema Heller si consta intr-un sistem de condensare cu suprafata de schimb de caldura si injectie de apa. In cazul sistemului Heller, diferentele mici intre temperatura apei de racire la intrarea in condensator (apa de injectie) si temperatura aerului atmosferic, respectiv intre temperatura de condensare si temperatura apei de injectie, determina o valoare mare a suprafetei de schimb de caldura a radiatorului, deci un gabarit mare al instalatiei. De aceea se impun valori mai mari ale celor doua diferente de temperatura. Acest fapt conduce la presiuni de condensare a aburului mai mari decat in cazul grupurilor binare conventionale, prevazute cu sistem de condensare cu turn de racire si, implicit, la randamente mai mici ale instalatiei. In ciuda acestui dezavantaj, sistemul de condensare de tip Heller a fost preferat sistemului de condensare conventional deoarece lucreaza cu un consum redus de apa si poate fi adaptat sa functioneze pe o unitate mobila.

In cadrul lucrarii au fost analizate sase scheme termodinamice de grupuri binare, stabilite ca fiind utilizabile in transporturi. In scopul analizarii acestor scheme au fost realizate sase programe de calcul.

Schemele termodinamice analizate sunt urmatoarele:

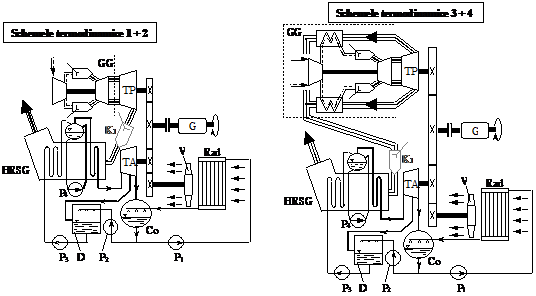
1.   TMG fara recuperator, TMA cu o singura treapta de presiune a aburului (fig. 3.1a, varianta fara K₁) - programul de calcul BINAR 1;

2.   TMG fara recuperator, camera de postcombustie, TMA cu o singura treapta de presiune a aburului (fig. 3.1a, varianta cu K₁) - programul de calcul BINAR 2;

3.   TMG cu recuperator, TMA cu o singura treapta de presiune a aburului (fig. 3.1b, varianta fara K₁) - programul de calcul BINAR 3;

4.   TMG cu recuperator, camera de postcombustie, TMA cu o singura treapta de presiune a aburului (fig. 3.1b, varianta cu K₁) - programul de calcul BINAR 4;

5.   TMG fara recuperator, TMA cu doua trepte de presiune a aburului (fig. 3.2a) - programul de calcul BINAR 5;

6.   TMG cu recuperator, TMA cu doua trepte de presiune a aburului (fig. 3.2b) - programul de calcul BINAR 6.

a) b)

Fig. 3.1.

a) b)

Fig. 3.2.

Notatiile din figurile 3.1 si 3.2 au urmatoarele semnificatii:

GG - generator de gaze

R - recuperatorul TMG

TP - turbina de putere, cu gaze

K₁ - camera de postcombustie

TA - turbina cu abur

G - generator electric

V - ventilator

Rad - radiator

CA - condensator

D - degazor

P₁.P₆ - pompe

CRGA - cazan recuperator generator de abur

3.3. Programele de calcul

In scopul analizarii din punct de vedere energetic a celor sase scheme termodinamice, au fost realizate sase programe de calcul, denumite BINAR 16. Ele pot fi cu usurinta unite intr-o varianta generala de program (de altfel realizata), asa cum s-a dorit initial, dar in acest caz durata rularii creste semnificativ iar utilizarea programului devine dificila. Pentru realizarea programelor de calcul a fost creata o biblioteca de subrutine (algoritme de calcul) concepute pentru calculul proceselor caracteristice grupurilor binare si pentru estimarea performantelor acestor grupuri. Aceste subrutine sunt:

COMPD - calculeaza procesul de comprimare dinamica in priza de admisie a TMG; calculul se face in calduri specifice medii variabile liniar cu temperatura;

COMPC - calculeaza procesul de comprimare in compresorul TMG; ca si in cazul subrutinei COMPD, calculul se face in calduri specifice variabile cu temperatura;

COMBL - efectueaza calculul procesului de combustie in camera de ardere a TMG; subrutina permite determinarea valorii coeficientului de exces de aer, compozitia produselor de ardere si coeficientii b_j, necesari calculului caldurilor specifice reale ale produselor de ardere;

DETECEN - calculeaza procesul de destindere in turbina generatorului de gaze; calculul se face in calduri specifice variabile, utilizand polinoame de gradul 5:

. (3.1)

Parametrul T din relatia (3.1) reprezinta temperatura absoluta a gazelor de ardere;

POSTCOMB - efectueaza calculul procesului de ardere in camera de postcombustie;

DETLIB - calculeaza procesul de destindere in turbina libera a TMG, utilizand metoda de calcul in calduri specifice variabile;

BILANT - efectueaza bilantul termic al CRGA si calculeaza valoarea debitului de apa/abur al cazanului, parametrii termodinamici dupa fiecare schimbator de caldura atat pe circuitul de gaze de ardere cat si pe cel de apa/abur precum si valoarea finala a presiunii apei/aburului;

DESTAB - calculeaza procesul de destindere in turbina cu abur;

DEGAZOR - subrutina calculeaza valorile entalpiei apei la intrarea/iesirea in/din degazor si debitele de abur la priza si condensator;

HELER - determina debitul de apa prin radiatorul condensatorului, cantitatea de caldura schimbata in radiator si debitul de aer necesar racirii apei in radiator;

APA, ASUM, ABUR - determina parametrii termodinamici ai apei, aburului saturat umed (inclusiv curba de saturatie), respectiv aburului supraincalzit;

PERFORMANTE - calculeaza parametrii de estimare a performantelor grupului binar.

Pentru realizarea subrutinelor COMPD, COMPC, COMBL, DETECEN, POSTCOMB si DETLIB au fost utilizate proceduri de calcul prezentate in [24], [31], [40] si [83]. Modul de determinare a parametrilor apei/aburului, caracteristic subrutinelor APA, ASUM si ABUR este prezentat in subcap. 3.3.1. Subrutinele BILANT, DESTAB, DEGAZOR, HELER si PERFORMANTE sunt, integral, realizari proprii, atat ca procedee de calcul cat si ca mod de transpunere in cod binar

Un program de analiza energetica corespunzator unei anumite scheme termodinamice de grup binar se realizeaza prin apelarea subrutinelor care descriu fiecare din procesele caracteristice grupului respectiv. Tipul subrutinelor apelate, ordinea de apelare a acestora si modul lor de legare depind de schema termodinamica a grupului analizat.

Pentru determinarea suprafetei de schimb de caldura a radiatorului a fost realizat programul de calcul CONDENSATOR. Acesta se poate atasa oricarui program din pachetul BINAR. Programele BINAR si condensator ruleaza in cascada, datele de iesire ale primului constituind date de intrare pentru cel de-al doilea.

Programul condensator este constituit din doua subrutine:

ALPHaer - calculeaza coeficientul de transfer de caldura prin convectie de la peretele metalic al tevillor radiatorului la aer

RADIATOR - calculeaza suprafeta de schimb de caldura a radiatorului condensatorului.

Subrutinele ALPHaer si RADIATOR constituie, de asemenea, realizari proprii, atat ca procedee de calcul cat si ca mod de transpunere in cod binar

Datele initiale, comune tuturor programelor de calcul din pachetul BINAR, sunt urmatoarele:

R_aer       - constanta aerului; ;

p_0, T₀ - presiunea si temperatura mediului ambiant; ;

H_i          - puterea calorifica inferioara a combustibilului; in toate calculele s-a considerat petrol de aviatie, avand ;

g_C, g_H2 - participatiile masice de carbon si hidrogen corespunzatoare combustibilului considerat; ;

j_ad - coeficientul pierderilor de presiune in dispozitivul de admisie al TMG; ;

G_a         - debitul de aer aspirat de TMG; ;

h_c - randamentul comprimarii; ;

q - raportul G_ar/G_a al aerului de racire al TMG; ;

ς - eficienta camerei de ardere a TMG; ;

ς₁          - eficienta camerei de postcombustie; ;

ν_K          - coeficientul de pierderi de presiune in camera de ardere a TMG; ;

h_m1 h_m2                  - randamentele mecanice ale turbinei generatorului de gaze, respectiv turbinei libere; ;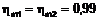

h_i1 h_i2 - randamentele interioare ale turbinei generatorului de gaze, respectiv turbinei libere; ;

h_ab - randamentul interior al turbinei cu abur; ;

ν_E1        - coeficientul de pierderi de presiune pe traseul de evacuare al turbinei libere a TMG; ;

Dt_g        - diferenta minima admisa intre temperatura gazelor de ardere la intrarea in supraincalzitorul CRGA si temperatura aburului supraincalzit furnizat de CRGA; ;

Dt_{eco m}  - diferenta minima admisa intre temperatura gazelor de ardere la intrarea in economizor si temperatura apei la iesirea din economizor; conform recomandarilor din [47] si [48], ;

t_ge         - temperatura gazelor de ardere la iesirea din CRGA; ;

t_abM      - valoarea maxima admisa a temperaturii aburului furnizat de CRGA; conform [47] si [48],;

p_p         - presiunea la priza de prelevare a aburului necesar degazarii apei; ;

Δt₁ - diferenta dintre temperatura apei la iesirea din radiator si temperatura mediului ambiant; ;

Dt₂       - diferenta dintre temperatura condensatului si temperatura aerului dupa radiator; ;

ν_g1        - valoarea initiala a coeficientului de pierderi de presiune a aerului in radiatorul condensatorului; ν_g1 = 0,98;

w_aer      - viteza de circulatie a aerului; .

Valorile parametrilor introdusi ca date initiale, precizate mai sus, nu constituie valorile extreme posibile in momentul de fata [6], [26], [84].

Din categoria datelor initiale fac parte si coeficientii care intervin in calculul caldurilor specifice functie de temperatura pentru aer (; ) si produsele de ardere (CO₂, H₂O, N₂, O₂), precum si caracteristicile constructive ale matricei suprafetelor de schimb de caldura considerate.

Dupa parcurgerea datelor initiale, programul apeleaza subrutinele de calcul a proceselor ce au loc in TMG. Succesiunea subrutinelor coincide cu succesiunea in care se desfasoara procesele (v. fig. 3.1 si fig. 3.2):

COMPD - COMPC - COMBL - DETECEN - DETLIB .

Legarea acestor subrutine se face prin egalarea parametrilor de stare la sfarsitul unui proces cu parametrii de stare la inceputul procesului urmator. Concret, presiunea si temperatura la iesirea dintr-o subrutina devin valori de start ale subrutinei urmatoare.

Dezvoltarea programelor de calcul dupa rularea subrutinei DETLIB depinde de prezenta sau absenta recuperatorului TMG. Pentru exemplificare, este prezentat in continuare programul BINAR 4, care presupune apelarea tuturor subrutinelor realizate. Indicii corespunzatori sectiunilor de curgere, atat pe partea de aer/gaze cat si pe partea de apa/abur sunt precizati in fig. 3.3a. Reprezentarea in diagrama T-s a procesele termodinamice corespunzatoare acestei variante de grup binar poate fi urmarita in fig. 3.3b.

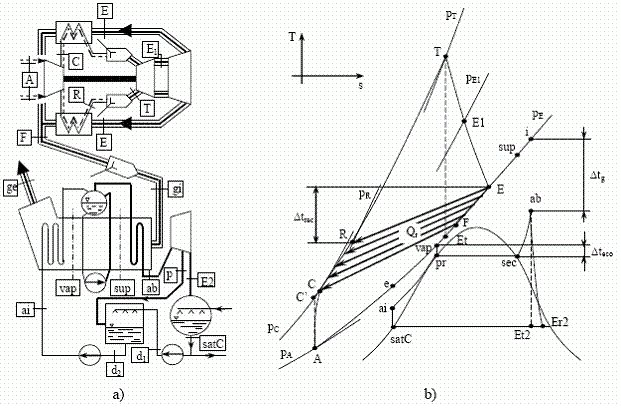
Fig. 3.3.

Subrutina DETLIB furnizeaza valoarea temperaturii in punctul E al ciclului (T_E). Temperatura aerului in punctul R (dupa recuperatorul TMG) este (v. fig. 3.3b):

(3.2)

In functie de temperaturile aerului in punctele C (furnizata de subrutina COMPC) si R, se determina cantitatea de caldura preluata de aer in recuperatorul TMG care este egala cu cantitatea de caldura cedata de gazele de ardere in recuperator. Din aceasta conditie de egalitate rezulta temperatura gazelor de ardere in punctul F, care marcheaza iesirea gazelor de ardere din TMG si intrarea lor in CRGA. Cunoscand temperatura gazelor de ardere in punctul F, se determina gradul de recuperare al recuperatorului TMG, dupa care se apeleaza subrutina POSTCOMB. Urmeaza apelarea subrutinei BILANT care permite efectuarea bilantului termic al CRGA si apoi apelarea, de doua ori la rand, a subrutinei DESTAB, in scopul calcularii procesului de destindere in turbina de la presiunea pe care o are aburul furnizat de CRGA pana la presiunea la priza de prelevare a aburului pentru degazare, respectiv de la presiunea la priza pana la presiunea din condensator. Subrutinele BILANT si DESTAB sunt prezentate in subcap. 3.3.2, respectiv 3.3.3. Dupa subrutina DESTAB sunt apelate succesiv subrutinele DEGAZOR (prezentata in subcap. 3.3.4) si HELER (prezentata in subcap. 3.3.5) care analizeaza procesele ce au loc in degazor, respectiv in condensator si in radiatorul acestuia. Dupa subrutina HELER se apeleaza subrutina PERFORMANTE (prezentata in subcap. 3.3.8), apoi se trece la calculul suprafetei de schimb de caldura a radiatorului condensatorului. In acest scop se apeleaza subrutinele ALRHaer (prezentata in subcapitolul 3.3.6) si RADIATOR (prezentata in subcapitolul 3.3.7), care constituie programul CONDENSATOR. La final, sunt prezentate rezultatele calculelor.

Programele de analiza corespunzatoare celorlalte scheme de instalatii avute in vedere in cadrul lucrarii sunt realizate in mod similar programului BINAR 4. In cazul variantelor in care TMG nu este prevazut cu recuperator (schemele termodinamice 1, 2 si 5), dupa prima apelare a subrutinei DETLIB se trece direct la apelarea subrutinei POSTCOMB (schema 2) sau a subrutinei BILANT (schemele 1 si 5).

3.3.1. Determinarea parametrilor termodinamici ai apei si aburului

Parametrii termodinamici ai apei si aburului se determina in cadrul subrutinelor APA, ASUM si ABUR, relatiile de calcul fiind preluate din [62].

Entalpia si volumul specific al apei se calculeaza, in functie de presiune si temperatura, cu formulele

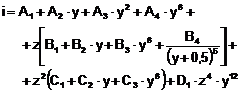[kJ/kg], (3.3)

respectiv

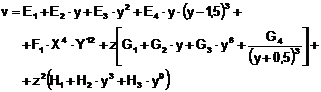[m³/kg], (3.4)

unde y = t/100 si z = (500-p)/100; t si p sunt temperatura [˚C], respectiv presiunea apei [bar].

Valorile coeficientilor din relatiile (3.3) si (3.4) sunt date in tabelul 3.1.

Tabelul 3.1

Presiunea de saturatie a apei se exprima in functie de temperatura de saturatie (t_s) ca

, (3.5)

in care .

Valoarea temperaturii de saturatie a apei in functie de presiune este data de expresia

. (3.6)

Entalpia, volumul specific si entropia apei la saturatie in functie de temperatura se calculeaza cu formulele

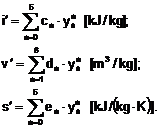(3.7)

Proprietatile aburului saturat uscat in functie de temperatura sunt date de

(3.8)

unde este constanta pentru vapori.

Constantele numerice din relatiile (3.5)(3.8) sunt date in tabelul 3.2.

Determinarea tuturor parametrilor aburului umed necesita cunoasterea, pe langa presiune si temperatura, a entropiei sau entalpiei aburului. Astfel, calculand mai intai titlul aburului

sau , (3.9)

se pot determina volumul specific si entalpia, respectiv entropia:

(3.10)

Tabelul 3.2

Pentru calculul entalpiei, entropiei si volumului specific al aburului in functie de presiune si temperatura s-au folosit relatiile:

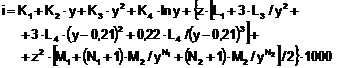, (3.11)

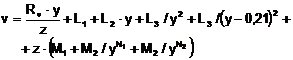, (3.12)

respectiv

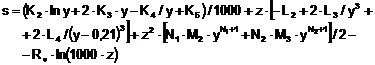, (3.13)

in care: .

Coeficientii care apar in relatiile (3.11)(3.13) sunt dati in tabelul 3.3.

Tabelul 3.3

3.3.2.   Bilantul termic al CRGA

Bilantul termic al CRGA se efectueaza in cadrul subrutinei BILANT. Procedura de calcul caracteristica acestei subrutine a fost stabilita pe baza informatiilor din [2], [21], [35], [38], [45], [46], [64] si [78]. In cazul CRGA cu doua trepte de presiune a aburului, au fost utilizate si informatii date in [15], [54], [65], [66].

Datele de intrare ale subrutinei BILANT sunt:

debitul de gaze de ardere furnizat de TMG - D_gm; se calculeaza in cadrul subrutinei COMBL;

temperaturile gazelor de ardere la intrarea/iesirea in/din CRGA - p_gi, T_gi (furnizate de subrutina DETLIB), respectiv p_ge, T_ge; in toate calculele s-au considerat si ;

temperatura apei de alimentare - T_ai (t_ai);

presiunea aburului furnizat de CRGA - p_ab;

presiunea pana la care se destinde aburul in turbina cu abur (presiunea in condensator) - p_satC;

diferenta impusa intre temperatura gazelor de ardere la intrarea in economizor si temperatura apei la iesirea din economizor - Δt_{eco i}.

Atat pierderile de presiune ale apei in economizor cat si cele ale aburului in supraincalzitor sunt de 5%. CRGA fiind cu circulatie fortata multipla, pierderile de presiune in vaporizator sunt acoperite de pompele de circulatie.

Pentru determinarea parametrilor termodinamici in puncte situate in domeniul apei si aburului supraincalzit se apeleaza subrutinele APA, respectiv ABUR. Determinarea parametrilor termodinamici in puncte situate pe curba de saturatie si in interiorul acesteia se realizeaza prin apelarea subrutinei ASUM..

In cazul grupurilor binare cu o singura treapta de presiune a aburului (variantele 1.4), temperatura initiala a aburului supraincalzit produs de CRGA se determina cu relatia

. (3.14)

Daca in urma calculului rezulta t_abi > t_abM = 560˚C, se impune t_abi = t_abM. Valoarea initiala a presiunii aburului supraincalzit se determina cu ecuatia polinomiala

[bar] (3.15)

stabilita in functie de perechile uzuale de parametri presiune/temperatura. Daca temperatura aburului scade sub 175˚C, presiunea rezultata din calcul risca sa creasca peste presiunea de saturatie corespunzatoare temperaturii t_ab, ceea ce ar conduce la situatia imposibila in care punctul descris de parametrii p_ab, t_ab s-ar afla in domeniul aburului saturat. Asadar, relatia (3.15) este valabila numai pentru (conditia de abur supraincalzit).

Din relatia (3.15) rezulta ca presiunea maxima a aburului supraincalzit are valoarea .

In functie de t_ai, p_abi si t_abi se determina entalpiile apei de alimentare (i_ai), apei la saturatie (i′), aburului saturat uscat (i″) si aburului supraincalzit (i_ab).

Din ecuatia bilantului termic al CRGA (v. fig. 3.4)

(3.16)

se poate determina debitul de abur:

[kg/s]. (3.17)

In aceste relatii, c_pgi si c_pge reprezinta caldurile specifice ale gazelor de ardere la intrarea/iesirea in/din CRGA.

Cunoscand valoarea lui D_a, se pot calcula cantitatile de caldura schimbate in supraincalzitor, vaporizator respectiv economizor:

;

; (3.18)

.

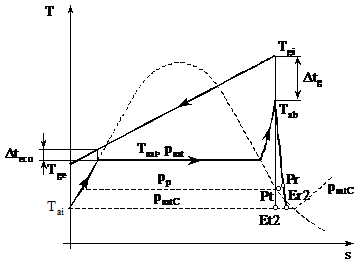
Fig. 3.4.

Ecuatia de bilant termic a supraincalzitorului are urmatoarea forma:

. (3.19)

In aceasta relatie, T_gs si c_pgs reprezinta temperatura, respectiv caldura specifica a gazelor de ardere dupa supraincalzitor (inainte de vaporizator). Temperatura T_gs se determina iterativ, plecand de la valoarea initiala si reducand treptat aceasta valoare cu 0,25 grd pana cand conditia de egalitate din ecuatia de bilant este satisfacuta. In mod analog se determina si T_gv - temperatura gazelor de ardere dupa vaporizator (inainte de economizor).

In acest punct al algoritmului de calcul este verificata conditia

, (3.20)

unde T_sat [K] reprezinta temperatura de saturatie (temperatura din tamburul CRGA).

Daca aceasta conditie nu este indeplinita, se reduce t_ab cu 0,25 grd si subrutina BILANT este reluata. In momentul in care conditia (3.20) este indeplinita, sunt retinute valorile finale ale parametrilor p_ab, D_a, T_gs si T_gv, care constituie datele de iesire ale subrutinei BILANT.

In cazul grupurilor binare cu doua trepte de presiune a aburului (variantele 5 si 6), treapta de inalta presiune furnizeaza abur supraincalzit cu temperatura t_abi. Impunand conditia , din bilantul termic al treptei de inalta presiune a CRGA rezulta temperatura gazelor de ardere la iesirea din treapta de inalta presiune / intrarea in treapta de joasa presiune. Procedeul de stabilire a parametrilor aburului de joasa presiune este cel descris in cazul schemelor termodinamice 14. Acesti parametri au valorile maxime care permit indeplinirea conditiei (3.20) in cazul treptei de joasa presiune.

3.3.3.   Procesul de destindere in turbina cu abur

Procesele de destindere reala si teoretica care au loc intr-o turbina cu abur sunt prezentate si analizate in [30], [41], [46], [55]. Asa cum s-a precizat anterior, calculul destinderii in turbina cu abur a grupului binar este realizat de subrutina DESTAB.

In cadrul subrutinei DESTAB, se considera ca aburul se destinde in turbina in doua etape: de la p_ab pana la presiunea corespunzatoare prizei de prelevare a aburului necesar degazarii apei (p_p), respectiv de la p_p pana la p_satC. Cele doua procese de destindere se desfasoara succesiv.

Entropia aburului supraincalzit la iesirea din CRGA/intrarea in turbina se noteaza cu s_ab. In cadrul subrutinei DESTAB, punctele ce caracterizeaza sfarsitul proceselor teoretic si real de destindere se noteaza generic Et respectiv Er; presiunea pana la care se face destinderea se noteaza cu "p". Particularizand, Et, Er si p se concretizeaza in Pt, Pr si p_p in cazul primei destinderi, respectiv Et2, Er2 si p_satC in cazul celei de-a doua destinderi (v. fig. 3.4). Entalpia si entropia apei la saturatie, corespunzatoare presiunii p, sunt notate i′, respectiv s′. Entalpia si entropia aburului saturat uscat, corespunzatoare aceleiasi presiuni, sunt notate i″, respectiv s″. In functie de relatia care exista intre s_ab si s″ sunt doua cazuri distincte:

CAZUL I. s_ab s″

In aceasta situatie punctul Et se afla situat in domeniul aburului supraincalzit sau, la limita, pe curba de saturatie (s_Et = s_ab s″), iar punctul Er se afla situat in domeniul aburului supraincalzit.

Temperatura in punctul Et se determina iterativ, pornind de la valoarea initiala . In functie de t_Et si de p, prin apelarea subrutinei ABUR se determina valoarea s_Et. Valoarea lui t_Et se reduce cu cate un grad pana in momentul in care este indeplinita conditia

. (3.21)

Cu valoarea finala a entalpiei in punctul Et (i_Et), corespunzatoare valorii finale a lui t_Et, se determina caderea termica disponibila

. (3.22)

Caderea termica interna se calculeaza cu relatia

. (3.23)

Cunoscand caderea termica interna, se poate determina entalpia in punctul Er:

. (3.24)

CAZUL II. s_ab < s″

In aceasta situatie punctul Et se afla situat in interiorul curbei de saturatie. Cunoscand presiunea si entropia la sfarsitul destinderii teoretice (p si s_Et), prin apelarea subrutinei ASUM se determina temperatura de saturatie, titlul (x_Et) si entalpia (i_Et) aburului saturat umed la sfarsitul procesului teoretic de destindere. Cunoscand entalpia in punctul Et, caderea termica disponibila se calculeaza cu relatia (3.22). Caderea termica interna se calculeaza cu relatia (3.23). Cunoscand caderea termica interna, cu relatia (3.24) se determina entalpia in punctul Er.

In continuare programul compara i_Er cu entalpia aburului saturat uscat (i″). Daca i_Er < i″, atunci punctul Er se afla situat in interiorul curbei de saturatie si subrutina DESTAB se incheie cu determinarea titlului aburului saturat umed in punctul Er (x_Er). Acest parametru este dat de subrutina ASUM. Daca i_Er i″, atunci punctul Er se afla situat in domeniul aburului supraincalzit; aceasta situatie nu poate fi acceptata in cazul destinderii finale (de la p_p pana la p_satC). In acest caz temperatura aburului furnizat de CRGA (t_ab) se reduce cu 0,25 grd si programul este reluat incepand de la subrutina BILANT. Procedura se repeta pana cand destinderea finala se termina in domeniul aburului umed.

3.3.4.   Analiza procesului termic din degazor

Degazorul este un schimbator de caldura prin amestec care, din punct de vedere termodinamic, are rol de preincalzitor de apa in cadrul instalatiei.

Subrutina DEGAZOR permite determinarea debitului de abur necesar degazarii apei (prelevat de la priza turbinei) si a debitului de abur condensat in condensator. Pentru realizarea subrutinei au fost folosite informatiile date in [19], [22], [52] si [70]. Intr-o prima faza, prin apelarea subrutinei ASUM, se determina presiunea de saturatie p_deg corespunzatoare temperaturii apei de alimentare (presiunea din degazor) si entalpia i_d2 a apei la saturatie, corespunzatoare presiunii p_deg (entalpia apei la iesirea din degazor). Entalpia apei la intrarea in degazor (i_d1) se calculeaza cu ajutorul subrutinei APA, in functie de p_deg si de temperatura de saturatie t_satC corespunzatoare presiunii de la condensator (temperatura apei la intrarea in degazor).

Ecuatia de bilant termic a degazorului este urmatoarea (v. fig. 3.5):

(3.25)

In aceasta relatie:

D_cd - debitului de abur condensat [kg/s];

D_p         - debitul de abur prelevat de la priza turbinei [kg/s];

i_Pr          - entalpia aburului la priza [kJ/kg]; valoarea sa este data de subrutina DESTAB.

Fig. 3.5.

Se face notatia

. (3.26)

Tinand cont de relatia

(3.27)

si de notatia (3.26), expresia (3.25) poate fi scrisa sub forma

. (3.28)

Din aceasta relatie rezulta:

. (3.29)

Cunoscand parametrul r, din relatiile (3.26) si (3.27) rezulta urmatoarele formule de calcul a debitelor:

[kg/s] (3.30)

3.3.5.   Analiza proceselor caracteristice instalatiei de condensare

Aceasta analiza se realizeaza in cadrul subrutinei HELER. Subrutina calculeaza debitul de apa prin radiatorul condensatorului (D_h), debitul de aer necesar racirii apei (D_aer) si cantitatea de caldura schimbata in radiator (Q_aer).

Datele de intrarea ale acestei subrutine sunt: Δt₁, Δt₂, t_satC, entalpia aburului la iesirea din turbina (i_Er2), entalpia apei la saturatie corespunzatoare presiunii p_satC (i′_C) si presiunea apei in radiator (p_h). In toate calculele efectuate s-a considerat p_h = p₀.

Valorile temperaturilor aerului incalzit (dupa radiator) si a apei racite in radiator sunt:

(3.31)

In functie de p_h si t_h se determina entalpia apei racite in radiatorul condensatorului (i_h). Cunoscand aceasta valoare, din ecuatia de bilant termic al condensatorului se calculeaza debitul de apa prin radiator (D_h) si raportul intre acest debit si debitul de abur la condensator. Relatiile de calcul sunt urmatoarele (v. fig. 3.5):

; . (3.32)

Cantitatea de caldura schimbata in radiatorul condensatorului se calculeaza cu relatia:

. (3.33)

Caldurile specifice ale aerului inainte si dupa radiator sunt date de relatiile:

[kJ/(kg∙K)]. (3.34)

Cu aceste marimi se poate determina debitul de aer necesar racirii condensatului:

[kg/s]. (3.35)

Marimile D_h, Q_aer si D_aer constituie datele de iesire ale subrutinei HELER.

3.3.6. Calculul coeficientului de schimb de caldura prin convectie

de la aer la peretele tevii

Coeficientul de schimb de caldura prin convectie de la aer la peretele tevii se calculeaza in cadrul subrutinei ALPHaer, cu formula

, (3.36)

data in [59] si [60], in care:

λ_aer               - conductivitatea termica medie a aerului [W/mּK];

ν_aer                - viscozitatea cinematica medie a aerului [m²/s];

Pr_aer - criteriul Prandtl pentru aer;

C_z                  - corectie care depinde de numarul de randuri de tevi intalnite de gaze in deplasarea lor; daca , atunci ; daca , C_z se calculeaza cu relatia

(3.37)

C_s                  - coeficient de corectie dependent de asezarea tevilor in fascicul; este dat de relatia:

.         (3.38)

Conductivitatea termica medie a aerului, viscozitatea cinematica medie si criteriul Prandtl se determina cu relatiile

; (3.39)

; (3.40)

, (3.41)

in care 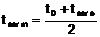si valabile pentru .

3.3.7.   Calculul suprafetei radiatorului

Radiatorul condensatorului este conceput ca un schimbator de caldura apa-aer, in contracurent. Apa racita in radiator este trimisa spre sistemul de injectie al condensatorului de amestec CA (v. fig. 3.5). Calculul suprafetei radiatorului se face in cadrul subrutinei RADIATOR, utilizand procedurile clasice de calcul care sunt prezentate in literatura de specialitate - [32], [60], [61], [75] si [86].

Datele de intrare ale subrutinei RADIATOR sunt: p₀, t₀, t_{aer e}, t_sat2, t_h, Q_aer si n_g1.

Radiatorul condensatorului are la baza modulul din tevi prezentat in fig. 3.6.

Pentru determinarea suprafetei de schimb de caldura a radiatorului condensatorului se utilizeaza relatia:

,                (3.42)

in care k_rad [W/m²ּK] reprezinta coeficientul global de schimb de caldura al radiatorului, iar Δt_{m lg} este diferenta medie logaritmica de temperatura; aceasta din urma se calculeaza cu formula

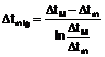, (3.43)

unde Δt_M, Δt_m reprezinta diferenta mare, respectiv diferenta mica intre temperaturile agentilor calculate la capetele suprafetei radiatorului.

Fig. 3.6.

Coeficientul global de schimb de caldura al radiatorului se calculeaza cu relatia

, (3.44)

in care coeficientul de eficienta termica a schimbului convectiv de caldura are valoarea .

Dupa determinarea suprafetei de schimb de caldura se calculeaza caderea de presiune pe radiator, pe partea aerului:

. (3.45)

In aceasta relatie, ζ reprezinta coeficientul de rezistenta gazodinamica. In cazul unui fascicul de tevi netede, dispuse alternant, coeficientul de rezistenta gazodinamica se calculeaza cu relatia

, (3.46)

in care s-a notat cu z_g numarul de randuri de tevi pe directia de curgere a aerului..

Coeficientul de rezistenta al unui rand de tevi, ζ₀, se calculeaza cu formula:

. (3.47)

In aceasta formula:

Re_aer - criteriul Reynolds pentru aer; se calculeaza cu relatia

;             (3.48)

C_s1 - coeficientul de forma al fasciculului cu tevi alternante; se exprima ca

; (3.49)

Parametrul φ_σ care intervine in relatia (3.49) depinde de pasii relativi

transversal - _e;

longitudinal - _e;

diagonal - ,

avand urmatoarea formula de calcul:

. (3.50)

Valoarea lui Δp_aer rezultata din calcul permite determinarea coeficientului de pierderi de presiune a aerului in radiator:

. (3.51)

Se impune urmatoarea conditie:

. (3.52)

Daca aceasta conditie nu este respectata, valoarea calculata a coeficientului de pierderi de presiune devine valoare initiala () si calculul de dimensionare a radiatorului este reluat. In momentul in care conditia (3.52) este satisfacuta, se trece la la urmatoarea etapa a calculului. Datele de iesire ale subrutinei RADIATOR sunt valorile finale ale suprafetei de schimb de caldura si coeficientului de pierderi de presiune.

3.3.8. Estimarea performantelor grupurilor cogenerative binare

pentru transport terestru

Parametrii de estimare a performantelor grupurilor binare, calculati in cadrul subrutinei PERFORMANTE, sunt:

Puterea dezvoltata de TMG; relatia de calcul, stabilita dupa [27] si [56] este

, (3.53)

unde e_TP reprezinta energia specifica dezvoltata de turbina de putere [kJ/kg]; este data de subrutina DETLIB;

Puterea dezvoltata de TMA; tinand cont de informatiile din [46], [48] si [79] s-a stabilit relatia de calcul

, (3.54)

in care:

D_{a IP}, D_{a JP}     - debitul de abur de inalta, respectiv joasa presiune livrat de CRGA [kg/s];

i_IP, i_JP - entalpia aburului de inalta, respectiv joasa presiune [kJ/kg].

In cazul variantelor 1.4, D_{a JP} = 0.

Puterea totala dezvoltata

. (3.55)

Consumul total de combustibil

, (3.56)

unde:

G_c, G_c1 - consumul de combustibil in camera de ardere a TMG, respectiv in camera de postcombustie [kg/s];

α₁                 - coeficientul de exces de aer dupa camera de postcombustie; se calculeaza in cadrul subrutinei POSTCOMB.

In cazul variantelor 1, 3, 5 si 6, G_c1 = 0 si α₁ = α..

Consumul specific de combustibil

. (3.57)

Randamentul TMG; relatia de calcul a acestui parametru, stabilita pe baza informatiilor din [44] si [56], este

, (3.58)

in care

e_T1 - energia specifica dezvoltata de turbina generatorului de gaze [kJ/kg]; se calculeaza in cadrul subrutinei DETECEN;

e_C - energia specifica consumata de compresorul TMG [kJ/kg]; se determina in cadrul subrutinei COMPC;

e_ar                 - energia specifica a aerului de racire [kJ/kg]; valoarea sa este data de subrutina COMPC;

i_T - entalpia gazelor de ardere la intrarea in turbina generatorului de gaze [kJ/kg comb];

i_R - entalpia aerului la intrarea in camera de ardere a TMG [kJ/kg comb].

Randamentul TMA; conform [79],

, (3.59)

unde i_gi si i_ge sunt entalpiile gazelor de ardere la intrarea, respectiv iesirea in/din CRGA.

Randamentul global se determina cu formula

, (3.60)

stabilita pe baza datelor prezentate in [28], [33], [56] si [58].

3.4. Analiza rezultatelor

Principalii parametri care influenteaza performantele grupurilor binare sunt:

temperatura gazelor de ardere dupa camera de ardere a TMG - T_T;

raportul de comprimare al compresorului - ε;

presiunea la care se produce condensarea aburului - p_satC;

temperatura apei de alimentare a CRGA - t_ai;

valoarea minima impusa pentru diferenta intre temperatura gazelor de ardere la intrarea in economizor si temperatura apei la iesirea din economizor - Δt_{eco i;}

temperatura gazelor de ardere dupa camera de postcombustie (in cazul variantelor de grupuri binare 2 si 4 - v. subcap. 3.2) - T_T1 ();

diferenta de temperatura la care opereaza recuperatorul TMG (in cazul variantelor de grupuri binare 3, 4 si 6) - .

Parametrii supusi analizei sunt:

randamentul global - η;

suprafata specifica de schimb de caldura a radiatorului; este data de raportul

; (3.61)

consumul specific de combustibil - g_sp;

masa specifica a radiatorului; este data de relatia

, (3.62)

unde m_R este masa relativa a matricii de baza a radiatorului instalatiei de condensare: (v. subcap. 3.3.7, fig 3.6).

3.4.1. Rezultatele analizei schemei termodinamice 1

Rezultate ale acestei analize sunt prezentate in [7], [8] si [9].

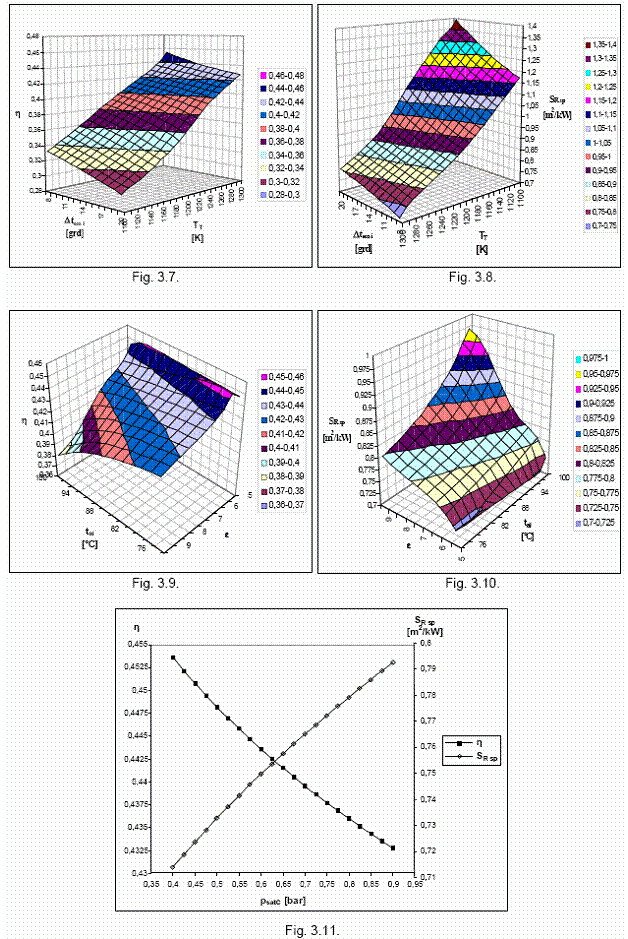
a) Influenta parametrilor T_T si Δt_{eco i} asupra performantelor si gabaritului grupului

Analiza a fost realizata in urmatoarele conditii: . Variatiile η si S_{R sp} in functie de T_T si Δt_{eco i} sunt prezentate in fig. 3.7 si 3.8.

Cresterea temperaturii T_T si reducerea diferentei de temperatura Δt_{eco i} sunt benefice atat din punct de vedere al performantelor instalatiei cat si din punct de vedere al gabaritului radiatorului: η creste (fig. 3.7) in timp ce S_{R sp} scade (fig. 3.8).

Prin urmare, asa cum era de asteptat, valorile optime ale parametrilor T_T si Δt_{eco i} sunt 1300 K, respectiv 8 grd (maxima, respectiv minima admise). In acest caz, parametrii analizati au urmatoarele valori:

; ;

; .

b) Influenta parametrilor t_ai si ε

Analiza a fost realizata considerand si valorile optime si , determinate la punctul "a". Programul de calcul corespunzator schemei

termodinamice 1 nu poate fi rulat pentru deoarece se ajunge la situatia in care , ceea ce face ca relatia (3.6) sa nu mai poata fi utilizata. De altfel, valorile nu sunt favorabile. Suprafetele de variatie prezentate in fig. 3.9 si 3.10 indica faptul ca punctul optim, din punct de vedere al performantelor grupului binar (η), este cel descris de si (valori impuse la punctul "a"). In conditiile analizei, cresterea lui ε conduce la imbunatatirea performantelor TMG. Deoarece T_T are o valoare impusa, temperatura gazelor evacuate din TMG scade (in acest caz, ). Atat timp cat aceasta temperatura permite producerea aburului in CRGA la parametrii maximi admisi (163 bar si 560˚C), performantele TMA sunt aceleasi. Asadar, pe ansamblu, performantele grupului binar se imbunatatesc datorita imbunatatirii performantelor TMG. Incepand cu o anumita valoare (optima) a lui ε, temperatura gazelor de ardere evacuate din TMG nu mai permite producerea aburului la parametrii maximi admisi, valorile acestora scazand continuu pe masura ce ε creste. In aceasta situatie, reducerea performantelor TMA este mai rapida decat imbunatatirea performantelor TMG, ceea ce conduce la reducerea performantelor grupului binar.

Atunci cand , valoarea optima a lui ε este 5,5; daca , atunci valoarea optima este valoarea minima considerata in calcule si anume 5.

Variatia temperaturii t_ai influenteaza performantele grupului binar in mod similar: pentru o anumita valoare a lui ε, exista o valoare limita a lui t_ai care permite producerea aburului la parametrii maximi admisi. Cresterea lui t_ai peste valoarea limita determina reducerea performantelor grupului binar.

Atunci cand si , gabaritul grupului binar nu este minim (v. fig. 3.10). S_{R sp} are insa o valoare apropiata de valoarea minima obtinuta in cadrul analizei.

c) Influenta presiunii p_satC

Analiza a fost facuta considerand pentru T_T, Δt_{eco i}, t_ai si ε valorile optime stabilite la punctele "a" si "b", anume 1300 K, 8 grd, 80˚C si 5,5. In mod logic, cresterea p_satC determina reducerea performantelor grupului binar (η scade - v. fig. 3.11). Evident, valoarea optima, din punct de vedere al performantelor, este valoarea minima considerata in calcule - . Estimarile preliminare au indicat faptul ca temperaturi ale condensatului mai mici de 76˚C (corespunzand presiunii de condensare de aproximativ

0,4 bar) determina dificultati in realizarea radiatorului condensatorului datorita cresterii excesive a debitului de apa care trebuie vehiculat prin acesta. Valoarea este convenabila si din punct de vedere al gabaritului grupului binar, deoarece S_{R sp} are valoarea minima.

Se poate concluziona ca performantele grupului binar se imbunatatesc atunci cand temperatura T_T creste iar presiunea p_satC si diferenta de temperatura Δt_{eco i} scad. Prin urmare, valorile optime ale acestor parametri sunt valorile limita superioara, respectiv limita inferioare luate in considerare in analizele efectuate: ; ;. Rationamentul este valabil pentru toate variantele de grupuri binare analizate, motiv pentru care variatia η si S_{R sp} in functie de acesti trei parametrii nu va mai fi analizata in cazul celorlalte cinci scheme termodinamice de grupuri binare care urmeaza a fi discutate. In toate analizele ulterioare se vor considera pentru cei trei parametrii valorile limita (optime) precizate mai sus.

Influentele parametrilor t_pi si ε nu pot fi rezumate prin reguli unice de variatie general valabile, ca in cazul celor trei parametrii precizati mai sus. Dupa cum se va vedea in continuare, variatiile η si S_{R sp} in functie de ε si t_pi depind de schema termodinamica analizata.

3.4.2. Rezultatele analizei schemei termodinamice 2

Rezultatele analizei schemei termodinamice 2 sunt prezentate in [10].

a) Influenta parametrilor t_ai si ε

Influentele parametrilor t_ai si ε asupra performantelor grupurilor binare avand la baza schema termodinamica 2 si a gabaritului radiatorului acestora sunt prezentate in fig. 3.12 si 3.13. Conform precizarilor din subcap. 3.4.1, analiza a fost realizata in urmatoarele conditii: , si . Temperatura dupa camera de postcombustie are valoarea . In acest caz, cresterea lui t_ai de la 76˚C la 94˚C determina cresterea lui η. Aceasta evolutie se datoreaza scaderii continue a diferentei de temperatura Δt_eco, parametrii aburului produs de CRGA avand mereu valorile maxime admise. Cand , Δt_eco atinge valoarea minima admisa - . Daca temperatura t_ai creste peste 94˚C, respectarea conditiei impune reducerea continua a valorilor parametrilor aburului produs de CRGA, ceea ce conduce la reducerea performantelor TMA si, implicit, la reducerea performantelor grupului binar (η scade).

Variatia η in functie de ε nu este monotona. Indiferent de valoarea lui t_ai, η atinge valoarea maxima atunci cand .

Aspectele prezentate mai sus conduc la concluzia ca, in cazul schemei termodinamice 2, valorile optime (care permit obtinerea performantelor maxime) ale parametrilor t_ai si ε sunt 94˚C, respectiv 10. Corespunzator acestui punct de proiectare optim, parametrii analizati au urmatoarele valori:

; ;

; .

Variatia S_{R sp} in functie de t_ai si este prezentata in fig. 3.13. Se observa ca si sunt valori convenabile si din punct de vedere al gabaritului radiatorului, deoarece permit obtinerea unei valori a S_{R sp} foarte apropiata de minimul obtinut in cadrul analizei.

b) Influenta temperaturii T_T1

Variatiile η si S_{R sp} n functie de T_T1, in cazul in care si (valori optime stabilite la punctul a") sunt date in fig. 3.14. Deoarece postcombustia are loc dupa TMG, performantele TMG nu sunt influentate de T_T1. Cresterea temperaturii T_T1 de la 900 K la 950 K determina imbunatatirea

Fig. 3.12.                   Fig. 3.13.

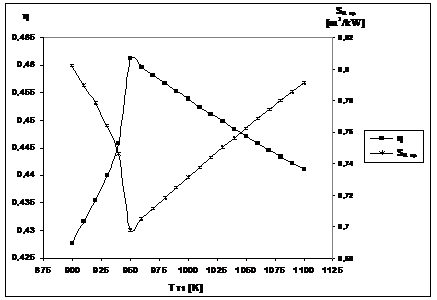
Fig. 3.14.

performantelor TMA deoarece cresc continuu valorile parametrilor aburului produs de CRGA. Cand , parametrii aburului ating valorile maxime admise iar . Daca T_T1 creste in continuare, parametrii aburului se mentin la valorile maxime admise, iar Δt_eco incepe sa creasca. Aceasta crestere determina reducerea continua a lui η. Asadar, valoarea optima a temperaturii T_T1 este valoarea minima care permite producerea aburului la parametrii maximi admisi si anume 950 K. Din acest motiv la punctul a" a fost impusa temperatura . Aceasta valoare permite, de asemenea, atingerea valorii minime a lui S_{R sp}.

3.4.3. Rezultatele analizei schemei termodinamice 3

Rezultate ale analizei schemei termodinamice 3 sunt prezentate in [11] si [12].

a) Influenta parametrilor t_ai si ε

Analiza s-a realizat pentru . Datorita recuperatorului TMG, temperatura gazelor de ardere evacuate din TMG (t_gi) este redusa, ceea ce face ca parametrii aburului produs de CRGA sa aiba valori scazute. De aceea, performantele TMA sunt reduse.

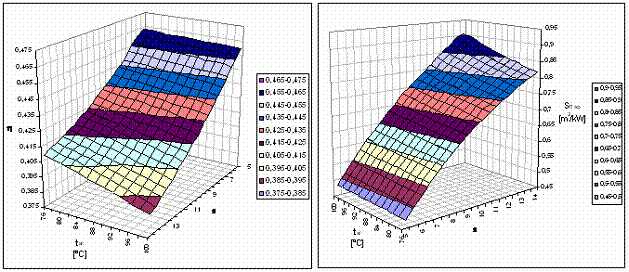Fig. 3.15.                   Fig. 3.16.

Fig. 3.17.

Cresterea lui ε de la 5 la 14 conduce la scaderea lui η (v. fig. 3.15). Temperatura t_ai nu influenteaza performantele TMG. Variatia η in functie de t_ai este determinata de performantele TMA, care se reduc atunci cand t_ai creste de la 76˚C la 100˚C.

In conditiile analizei, schema termodinamica 3 permite atingerea randamentului maxim atunci cand si . In acest caz,

; ;

; .

Valorile si sunt optime si din punct de vedere al gabaritului, valoarea S_{R sp} mentionata mai sus fiind valoarea minima obtinute in cazul acestei variante constructive de grup binar (v. fig. 3.16).

b) Influenta diferentei de temperatura Δt_rec

Analiza s-a realizat considerand valorile optime si , stabilite la punctul a".

Atunci cand ε si T_T sunt constante (situatia de fata), cresterea Δt_rec determina cresterea temperaturii gazelor evacuate din TMG, ceea ce determina reducerea performantelor TMG. Cresterea temperaturii gazelor evacuate din TMG (aceeasi cu temperatura la intrarea in CRGA - t_gi) determina cresterea valorilor parametrilor aburului produs de CRGA, ceea ce determina imbunatatirea performantelor TMA. Reducerea performantelor TMG este insa mai accentuata, rezultatul fiind reducerea randamentului global η (v. fig. 3.17).

Se poate concluziona ca punctul optim de proiectare este descris de valoarea minima . Calculele estimative nu au fost realizate pentru deoarece, in aceste situatii, suprafata S_r creste foarte mult, complicand mult realizarea TMG. Dupa cum se observa in fig. 3.17, convine si din punct de vedere al gabaritului radiatorului instalatiei de condensare, acesta fiind minim (S_{R sp} este minima).

3.4.4. Rezultatele analizei schemei termodinamice 4

Rezultatele acestui studiu sunt prezentate in [13] si [14].

a) Influenta parametrilor t_ai si ε

Analiza s-a realizat pentru si . Performantele TMG nu depind de t_ai, iar performantele TMA nu sunt influentate de ε. Pe langa variatiile indicatorilor de performanta ai TMA in functie t_ai si variatiile indicatorilor de performanta ai TMG in functie de ε, eficienta postcombustiei contribuie semnificativ la stabilirea profilului suprafetei . Cresterea lui ε de la 5 la 10 determina cresterea continua a η (v. fig. 3.18); curbele prezinta un maxim atunci cand , indiferent de valoarea lui ε. Valorile mai mari ale raporului de comprimare () sunt imposibile deoarece se ajunge la situatia in care (v. fig. 3.3b), ceea ce face imposibila functionarea recuperatorului TMG.

Cresterea randamentului η, atunci cand t_ai creste de la 76˚C la 94˚C, se datoreaza reducerii continue a diferentei de temperatura Δt_eco, in conditiile in care parametrii aburului supraincalzit produs de CRGA au valorile maxime admise. Cand , atunci . Cresterea in continuare a temperaturii t_ai conduce la reducerea valorilor parametrilor aburului produs de CRGA, Δt_eco mentinandu-se la valoarea minima admisa; performantele TMA se reduc si aceasta determina reducerea performantelor grupului binar. Asadar, si sunt valorile optime, care permit atingerea performantelor maxime in cazul schemei termodinamice 4. In acest caz, ; ;

; .

Variatia S_{R sp} in functie de t_ai si ε este prezentata in fig. 3.19. Se constata ca si sunt valori optime si din punct de vedere al gabaritului instalatiei de condensare, permitand obtinerea valorii minime a suprafetei S_{R sp}.

b) Influenta parametrilor T_T1 si Δt_rec

Studiul a fost efectuat considerand valorile optime si , stabilite la punctul a". Asa cum este normal, T_T1 nu influenteaza performantele TMG. Variatia T_T1 de la 900 K la 950 K

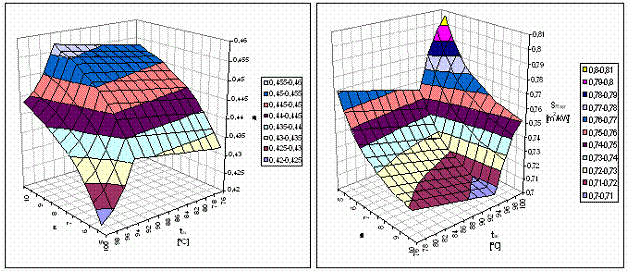Fig. 3.18. Fig. 3.19.

Fig. 3.20. Fig. 3.21.

determina cresterea parametrilor aburului supraincalzit, in conditiile in care . Aceasta conduce la imbunatatirea performantelor TMA care determina imbunatatirea performantelor grupului binar (η creste - v. fig. 3.20). Cand , parametrii aburului supraincalzit ating valorile maxime admise. Daca T_T1 creste in continuare, parametrii aburului supraincalzit raman neschimbati iar Δt_eco creste. De aceea, randamentul global η scade.

Evolutia η in functie de T_T1 indica faptul ca, analog schemei termodinamice 2, valoarea optima a temperaturii T_T1 este valoarea minima care permite producerea aburului la parametrii maximi admisi. In acest caz, .

Variatia Δt_rec in intervalul 50170 grd determina o usoara crestere liniara a lui η. Prin urmare valoarea sa maxima se atinge atunci cand . In conditiile analizei, nu sunt posibile valori deoarece recuperatorul TMG devine inoperant (ca si la punctul "a", se ajunge la )

Dupa cum se observa in fig. 3.21, S_{R sp} are valoarea minima atunci cand si . Prin urmare, aceste valori sunt optime atat din punct de vedere al performantelor cat si din punct de vedere al gabaritului instalatiei de condensare.

3.4.5. Rezultatele analizei schemei termodinamice 5

Deoarece atat recuperatorul TMG cat si camera de postcombustie lipsesc, este necesar a fi studiata doar influenta parametrilor t_ai si ε asupra performantelor si gabaritului grupurilor binare avand la baza acesta schema.

Fig. 3.22. Fig. 3.23.

Variatia t_ai influenteaza nesemnificativ performantele grupurilor binare avand la baza aceasta schema. Astfel, cresterea t_ai de la 76 la 100 conduce la o usoara scadere a lui η (v. fig. 3.22). Randamenul global maxim se obtine atunci cand si . In acest caz,

; ;

; .

Valoarea S_{R sp} precizata mai sus nu este minimul atins in cadrul analizei dar este foarte apropiata de acesta (diferenta sub 1%) - v. fig. 3.23.

3.4.6. Rezultatele analizei schemei termodinamice 6

a) Influenta parametrilor t_ai si ε

Studiul a fost realizat pentru .

Diferenta intre aceasta schema termodinamica si schema 3 consta in prezenta treptei de joasa presiune pe circuitul de apa/abur. Aceasta a doua treapta de presiune a aburului permite imbunatatirea performantelor TMA, ceea ce determina imbunatatirea performantelor grupului binar. Profilul suprafetei este asemanator celui obtinut in cazul schemei termodinamice 3 (v. fig. 3.24 si 3.15).

Similitudinile cu schema termodinamica 3 fac ca si in cazul schemei 6 atat performantele maxime cat si gabaritul minim al radiatorului (suprafata S_{R sp} minima - v. fig. 3.25) sa se obtina atunci cand si . In acest caz, valorile parametrilor analizati sunt urmatoarele:

; ;

; .

Fig. 3.24. Fig. 3.25.

b) Influenta diferentei de temperatura Δt_rec

Studiul s-a efectuat pentru valorile optime si , determinate la punctul "a". Ca si in cazul schemei 3, performantele maxime si gabaritul minim al radiatorului condensatorului se obtin atunci cand (v. fig. 3.26). Parametrul S_{R sp} are o evolutie asemanatoare celei care caracterizeaza schema termodinamica 3.

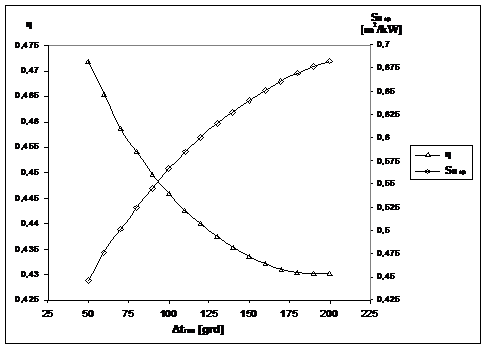
Fig. 3.26.

3.5. Concluzii asupra analizei energetice

Literatura de specialitate ofera in foarte putine cazuri date suficiente privind performantele grupurilor binare existente, astfel incat sa poata fi realizata comparatia cu datele rezultate in urma calculelor. In tabelul 3.4 sunt prezentati parametrii caracteristici pentru doua grupuri binare industriale care permit aceasta comparatie:

grupul de 480 MW aflat in functiune la Baglan Bay (Tara Galilor) din anul 2002, avand la baza TMG de tip GE-9H si care constituie cel mai performant grup binar din lume realizat pana in prezent; informatiile au fost preluate din [50], [84] si [94];

grupul de 384 MW prezentat in [73] si avand la baza TMG de tip ABB GT-26.

Din pacate, nici in putinele situatii care permit comparatia, nu se ofera informatii complete cu privire la performantele instalatiei. Astfel, in cazul grupului de 480 MW, lipsesc informatiile cu privire la consumul de combustibil.

Cele doua grupuri binare prezentate in tabelul 3.4 corespund schemei termodinamice 5. Aceasta schema (una dintre cele mai complexe) este cel mai frecvent utilizata in prezent, in varianta prezentata sau in variante usor modificate. Evident, grupurile binare industriale avand la baza aceasta schema prezinta sistem de condensare conventional, cu turn de racire.

Tabelul 3.4

Diferentele mici, de maxim 2,28%, intre valorile oferite in literatura de specialitate pentru parametrii de estimare a performantelor grupurilor binare si valorile calculate cu programul BINAR 5, certifica validitatea procedurii de calcul utilizate in cadrul programelor BINAR.

Pentru a facilita compararea celor sase scheme termodinamice analizate, valorile optime ale parametrilor caracteristici grupurilor binare avand la baza aceste scheme s-au centralizat in tabelul 3.5.

Tabelul 3.5

Se constata ca toate cele sase scheme permit realizarea unor grupuri binare cu performante superioare motoarelor diesel actuale de puteri echivalente (randamentul acestora nu depaseste 40% - [77]) dar inferioare performantelor grupurilor binare industriale de puteri mari, de ultima generatie. Acest fapt se datoreaza in principal valorilor foarte ridicate ale temperaturii T_T (pana la 1700 K - v. tabelul 3.4) la care lucreaza TMG de puteri mari, de ultima generatie si presiunilor p_satC foarte scazute (pana la 0,04 bar) la care opereaza sistemele de condensare conventionale, cu turn de racire, utilizate in cazul grupurilor binare industriale.

Rezultatele studiului privind grupurile binare cu postcombustie (schemele termodinamice 2 si 4) arata ca eficienta maxima a procesului de postcombustie se obtine atunci cand temperatura la sfarsitul acestui proces are valoarea minima care permite producerea aburului la parametrii maximi admisi. In conditiile prezentului studiu, valoarea optima a temperaturii de postcombustie este 950 K.

Valorile S_{R sp} precizate in tabelul 3.5 sunt mari, dar nu impiedica utilizarea grupurilor binare ca sisteme de propulsie feroviara. Ele pot fi acceptate chiar si in cazul autocamioanelor de mare tonaj. In cazul automobilelor, insa, aceste valori nu sunt admise. Utilizarea grupurilor binare ca sisteme de propulsie a automobilelor presupune gasirea unor solutii pentru reducerea gabaritului.

Atat performantele maxime cat si gabaritul minim al radiatorului se obtin in cazul schemei termodinamice 6 (grup binar avand TMG cu recuperator si TMA cu doua trepte de presiune a aburului - v. fig. 3.2b), atunci cand t_ai, ε si Δt_rec au valorile minime luate in calcul, anume ε = 5, t_pi = 76˚C si               Δt_rec = 50grd. In acest caz, S_{R sp} = 0,446 m²/kW si m_{R sp} = 0,446 kg/kW. Facand precizarea ca matricea radiatorului are suprafata relativa 111,56 m²/m³, rezulta ca volumul specific al radiatorului este v_sp = 4∙10^-3 m³/kW. Prin urmare, masa si volumul radiatorul instalatiei de condensare vor avea valorile efective 6960 kg / 16 m³ pentru un grup binar care dezvolta 4000 kW (domeniul tractiunii feroviare), 1218 kg / 2,8 m³ in cazul unui grup binar de 700 kW (domeniul autovehiculelor grele) si 174 kg / 0,4 m³ pentru un grup binar de 100 kW (cazul autoturismelor).

Valorile corespunzatoare tractiunii feroviare, desi mari, sunt acceptabile. Chiar si in cazul autovehiculelor grele, masa si volumul radiatorului au valori rezonabile. Solutii precum incadrarea partiala a radiatorului in structurile de caroserie pot reduce considerabil spatiul ocupat de radiator, marind astfel spatiul util. In cazul autoturismelor, insa, atat masa cat si volumul radiatorului depasesc limitele admise. Utilizarea grupurilor binare ca sisteme de propulsie a autovehiculelor impune gasirea unor solutii de reducere a masei si volumului radiatorului instalatiei de condensare. Cu alte cuvinte, se impune reducerea suprafetei specifice S_{R sp}.