|
|
|
Calculul barelor de greutate mare solicitate axial
In
rezistenta materialelor, aproape intotdeauna , efectul greutatii
proprii este neglijabil . In cazul barelor lungi ( cablurile de la ascensoare,
prajinile de foraj, pilele podurilor, turnurile farurilor ) greutatea
proprie este destul de mare deci trebuie sa se calculeze si sa
se tina seama de ea. Sa consideram o bara
cilindrica de lungime mare, suspendata si actionata la
capatul liber de o forta axiala concentrata P din
figura 76. Din 
( figura 77) ; ecuatia de echilibru a
partii izolate de lungime (x) rezulta: N(x)- G(x)- P = 0 N(x)= G(x) + P unde G(x)= 
si q =
este
forta distribuita pe unitatea de lungime a barei. Iar 
reprezinta
greutatea specifica a materialului din care este confectionata
bara. 
; 
; 
; 
, ( in cazul
particular in care P = 0;=0; si 
); 
; 
; Anec=
; relatia de dimensionare, a barei. Daca lungimea (l) creste mereu, se
ajunge la 
, ceea ce
duce la Anec=
, adica
o nedeterminare.
Deci,
daca lungimea barei creste mai mult 
se ajunge la situatia 
, adica greutatea proprie a
barei produce ruperea. 
este lungimea de rupere sub efectul
greutatii proprii. Lungimea
de rupere nu depinde de marimea sectiunii transversale , ci numai de
natura materialului si de limita de rupere. Alungirea sau scurtarea
totala se calculeaza cu relatia:
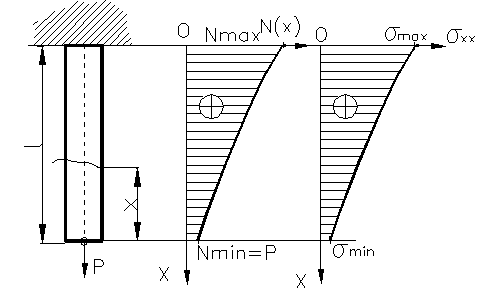
Figura 76
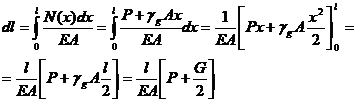
G= 
, reprezinta greutatea totala a barei.
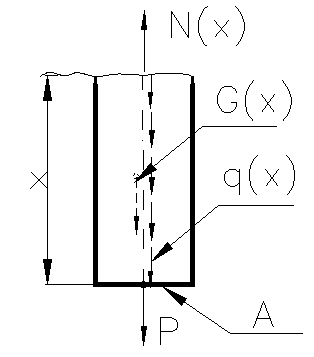
Figura 77
