
|
|
|
Utilizarea
Obiective operationale:
Dupa lectura acestui capitol, studentii ar trebui sa reuseasca sa:
elaboreze baza de date corespunzatoare studiului corelational
calculeze coeficientul de corelatie potrivit naturii variabilelor masurate
solutioneze problemele datelor lipsa
interpreteze rezultatele obtinute
Efectuarea unor studii experimentale nu este solutia potrivita pentru orice context de cercetare. In anumite situatii trebuie sa ne limitam la a stabilii relatii de covarianta existente intre doua sau mai multe variabile masurate. Reintorcandu-ne la exemplul de la modulul 4, sa presupunem ca ceea ce intereseaza echipa de cercetare este identificarea tulburarilor asociate lipsei activitatii fizice, concentrandu-se mai ales asupra obezitatii. Obezitatea a fost exprimata in numarul de kilograme deasupra celui prevazut conform varstei, genului si inaltimii. Sa presupunem (doar in scop didactic) ca datele obtinute intr-un studiu (n=20) sunt cele redate in tabelul de mai jos:
|
Subiecti |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
Nr. Ore/Saptamana |
5 |
5 |
2 |
3 |
7 |
5 |
4 |
3 |
6 |
2 |
8 |
4 |
5 |
6 |
4 |
5 |
6 |
2 |
3 |
4 |
|
Kg peste normal |
4 |
6 |
7 |
6 |
3 |
4 |
5 |
6 |
3 |
7 |
2 |
5 |
4 |
3 |
5 |
4 |
3 |
8 |
4 |
5 |
In baza de date vom definii doua variabile pentru cele doua variabile masurate (ore de activitate fizica pe saptamana si kg peste normal), ambele fiind de tip numeric. Pentru a calcula gradul de asociere al acestora vom recurge la calculul coeficientului de corelatie Pearson urmand sirul de comenzi Analyze→Correlate→Bivariate. In campul Variables vom introduce variabilele ce urmeaza a fi corelate, in cazul nostru cele doua variabile masurate. In continuare vom bifa coeficientul de corelatie ce urmeaza a fi calculat, in cazul de fata dat fiind ca ambele variabile sunt numerice vom opta pentru coeficientul Pearson. Semnificatia coeficientului de corelatie calculat o vom verifica printr-un test two-tailed. La Options se poate seta calculul unor componente partiale ale coeficientului standardizat de corelatia Pearson (covarianta, suma produselor) si date descriptive. Tot in aceasta sectiune putem seta strategia de management al datelor lipsa (discutia este relevanta doar in cazul a trei sau mai multe variabile).
In urma setarilor se apasa butonul OK si se obtine outputul prezentat mai jos.
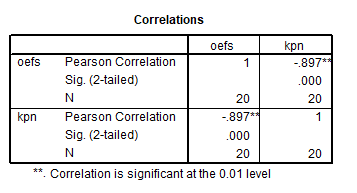
In fereastra Outputurilor este afisata matricea de corelatie. Din moment ce este o matrice simetrica, coeficientii prezentati de o parte si de alta a diagonalei principale sunt identici. Pe linii si pe coloane sunt prezentate aceleasi variabile. Se observa ca valoarea corelatiei intre oefs (ore exercitiu fizic saptamanal) si kpn (kilograme peste normal) este de r =-.897. Valoarea calculata a lui p este mai mica decit 0.01 (in table apare 0.000, ceea ce nu inseamna ca este 0). Probabilitatea ca sa se obtina doar datorita aleatorului o astfel de corelatie este mica, chiar foarte mica dar nu este zero. Pentru a evita o astfel de interpretare eronata, de obicei in prezentarea rezultatelor se trece 0.001.