
|
|
|
Registri de deplasare. Sumatoare. Unitati logico aritmetice.
1.1. Registre de deplasare
Primul circuit aritmetic prezentat este un registru de deplasare cu 8 intrari si 8 iesiri, ca in figura 2, 8 biti de intrare sunt prezenti pe liniile D0 ,, D7. Iesirea, care este intrarea deplasata cu un bit, este disponibila pe liniile S0 ,,S7. Linia de control C determina directia de deplasare, 0 pentru staga, 1 pentru dreapta. Pentru a vedea cum functioneaza circuitul trebuie sa remarcati perechile de porti AND pentru toti bitii cu exceptia portilor de la capete.
Cand C=1, membrul drept al fiecarei perechi este activat, transferand bitul de intrarecorespunzator la iesire. Deoarece poarta AND din dreapta este conectata la intrarea portii OR din dreapta sa, se va realiza o deplasare spre dreapta a bitului. Cand C=0 membrul stang al portii AND se va activa realizand o deplasare spre stanga.
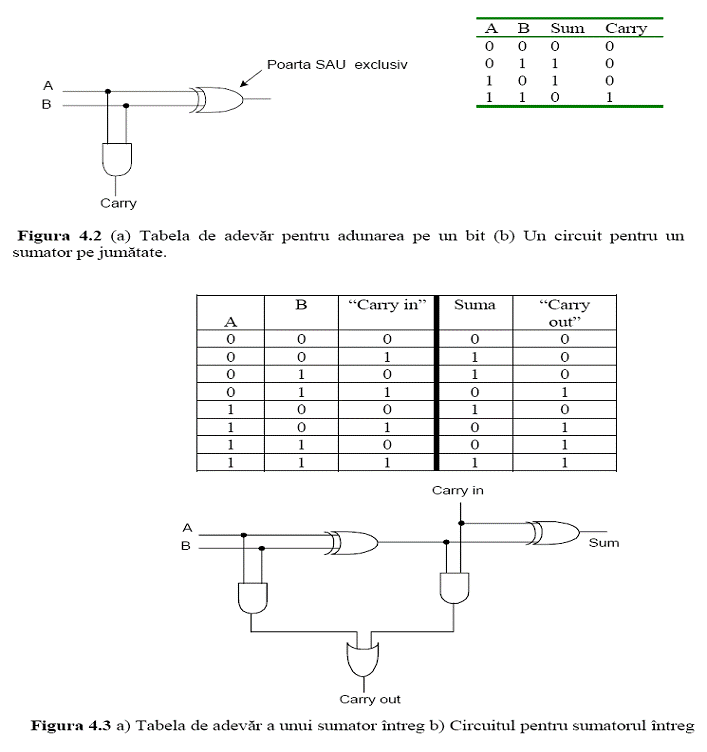
1.2. Sumatoare
Un calculator care nu poate aduna intregi este aproape de neconceput. In consecinta un circuit hard care realizeaza adunari este o parte esentiala a oricarui CPU. Tabela de adevar pentru adunarea intregilor pe 1 bit este prezentata in figura 2a. Sunt prezente doua iesri: suma intrarilor A si B, si transferul (carry) catre urmatoarea pozitie (spre stanga). Un circuit pentru calcularea atat a bitului suma, cat si a bitului de transport este ilustrat in figura 2b. Acest circuit simplu este cunoscut in general sub numele de "half adder" (sumator pe jumatate).
Desi un sumator pe jumatate este adecvat pentru adunarea bitilor de pondere mica a doua cuvinte de intrare multibit, el nu va face acest lucru pentru un bit pozitionat la mijlocul cuvantului deoarece el nu va folosi transportul de la rangul din dreapta. Ca solutie este nevoie de un sumator complet ca in figura 3. Din inspectarea circuitului, ar trebui sa reiesa clar ca un sumator complet este construit din 2 sumatoare pe jumatate. Linia de iesire "sum" este 1 daca un numar impar din bitii A, B si "carry in" sunt 1. Bitul "carry out" este 1 daca atat A cat si B sunt 1, sau numai unul din ei este 1 si bitul "carry in" este deasemenea 1. Impreuna cele 2 sumatoare pe jumatate genereaza atat bitul suma cat si bitul de transport.
Pentru a construi un sumator, sa zicem pentru doua cuvinte pe 16 biti, trebuie sa construim 16 replici ale circuitului din figura 3. Transportul unui bit "carry out" este folosit ca linie "carry in" pentru vecinul sau din stanga. Transportul la cel mai din dreapta bit este legat la 0.
Acest tip de sumator este denumit "ripple carry adder" (sumator cu propagare) deoarece in cel mai rau caz adaugand 1 la 11111 (binar), insumarea nu se completeaza pana cand transportul nu se propaga pe tot traseul de la cel mai din dreapta bit pana la cel mai din stanga bit.
Exista de asemenea, si sunt de obicei preferate, sumatoarele care nu prezinta aceasta intarziere, si care sunt mai rapide. Ca un exemplu simplu de sumator rapid considerati spargerea unui sumator pe 32 biti intr-unul pe 16 biti pentru prima jumatate si unul de 16 biti pentru jumatatea superioara. Cand incepe insumarea, sumatorul superior nu poate lucra deoarece nu va cunoaste transportul (carry in) timp de 16 insumari.
Oricum, luati in calcul aceasta modificare. In loc sa aveti o singura jumatate superioara, se poate realiza sumatorul cu 2 jumatati superioare in paralel duplicand hardware-ul pentru jumatatea superioara. Circuitul consta in 3 sumatoare pe 16 biti: unul pentru jumatatea inferioara si doua pentru cea superioara, U0 si U1, care ruleaza in paralel. Un zero este intodus in U0 ca transport (carry), iar in U1 este intodus 1 ca transport. Acum, ambele vor porni in acelasi timp cu partea inferioara, dar numai unul va fi corect. Dupa 16 cicluri de insumare se va cunoaste care este transportul in partea superioara, deci acum se poate selecta jumatatea superioara corecta din cele doua raspunsuri disponibile. Acest truc reduce timpul de insumare cu un factor de 2. Un astfel de sumator este denumit sumator cu selectia transportului (carry select adder). Acest truc poate fi repetat apoi pentru a construi fiecare sumator pe 16 biti din sumatoare pe 8 biti si asa mai departe.
1.3. Unitati logice aritmetice
Majoritatea computerelor contin un singur circuit pentru realizarea operatiilor AND, OR, NOT si SUM (insumare) a doua cuvinte masina. De obicei un astfel de circuit pentru cuvinte pe n biti este construit din n circuite identice pentru fiecare bit individual. Figura 4 este un exemplu simplu de astfel de circuit denumit ALU. Acesta poate calcula oricare din urmatoarele 4 functii: A AND B, A OR B, A+B, B , in functie de combinatia liniilor de intrare F0, F1: 00, 01, 10 sau 11. De remarcat ca A+B inseamna suma aritmetica a lui A si B, nu OR boolean.
Partea din stanga jos a ALU contine un decodificator pe 2 biti pentru a genera semnalele de control F0 si F1. In functie de valorile lui F0 si F1 numai unul din cele 4 linii este selectata.Setarea acestei linii permite ca iesirea din functia selectata sa ajunga la poarta OR pentru iesire. Partea din stanga sus contine logica de calcul pentru A AND B, A OR B si B negat, dar cel mult unul din aceste rezultate este trnsferat la poarta OR finala in functie de liniile de validare ce provin din decodor. Deoarece exact una din linii va fi 1, numai una din cele 4 porti AND ce conduc la poarta OR va fi validata, celelalte trei vor fi 0, independent de A si B. In plus pentru a putea utiliza A si B ca intrari pentru operatii logice si aritmetice, este de asemenea posibil sa se forteze la zero oricare din ele negand ENA sau ENB. Este de asemenea posibil sa se obtina A setand INVA. In conditii normale, ENA si ENB sunt ambele 1 si INVA va fi 0. In acest caz A si B sunt introduse in ALU fara modificari.
Coltul din dreapta jos al ALU contine un sumator complet pentru calcularea sumei dintre Asi B inclusiv manipularea bitilor de transport, deoarece este posibil ca astfel de circuite sa fie conectate impreuna pentru a realiza operatii la nivelul de cuvant. Circuite ca in figura 4 sunt disponibile si sunt cunoscute sub numele de "bit slices". Acestea permit proiectantului de calculatoare sa construiasca un ALU de orice marime doreste.