
|
|
|
Analiza spectrala a semnalelor de date in banda de baza.
1.1 INTRODUCERE TEORETICA
In cadrul acestui capitol se vor analiza spectrele semnalelor aleatoare. In continuare se vor considera cateva tipuri de semnale de date in banda de baza.
Analiza spectrala a unui semnal consta in exprimarea acestuia, analitic sau grafic, printr-o suma de functii cosinusoidale, precizand frecventele, amplitudinile si fazele acestora. Analiza spectrala a unui semnal se face su scopul de a determina banda de frecvente necesara pentru transmiterea acestuia pe un canal de telecomunicatii sau pentru a determina raspunsul circuitelor liniare la acest semnal.
Pentru analiza semnalelor periodice se utilizeaza seriile Fourier, iar pentru analiza semnalelor neperiodice transformata Fourier.
Deoarece semnalele periodice sunt exprimate prin sume discrete de semnale elementare de tip cosinusoidal sau exponential rezulta ca spectrele de amplitudini si cele de faza vor fi discrete, liniile spectrale asociate fiecarei componente existand numai la multiplii frecventei de repetitie.
Semnalele neperiodice, de durata finita, pot fi considerate ca un caz limita al semnalelor periodice, cu perioada tinzand la infinit. Cu cat perioada T a unui semnal devine mai mare, frecventa fundamentala devine tot mai mica, spectrul tot mai dens, iar amplitudinile componentelor spectrale din ce in ce mai mici. La limita nu se mai poate face o discriminare intre doua componente succesive, spectrul existand pentru orice w; spectrul discret devine un spectru continuu.
1.1.1 Semnale de date in banda de baza
IEEE de fineste "banda de baza" ca fiind banda de frecvente ocupata de un semnal (de date) inainte ca acesta sa moduleze un purtator (sau subpurtator) pentru a se obtine semnalul de transmis in linie sau semnalul radio. Un semnal de date in banda de baza este, prin urmare, un semnal de date asa cum el se prezinta la iesirea sau la intrarea unui echipament de prelucrare sau de prezentare a datelor.
Semnalul de date in banda de baza are un spectru de frecevente care incepe de la frecvente foarte joase (chiar de la frecventa zero). Un astfel de semnal poate fi transmis pe distante de ordinul sutelor si chiar miilor de metri pe liniile cu fire metalice, acestea avand o caracteristica de frecventa (de transfer) de tip trece jos, nefiind necesara deci o translatare a spectrului de frecvente. Distanta de transmisiune este limitata de cativa factori: atenuarea introdusa de linie, dependenta de caracteristicile liniei si de lungimea acesteia, zgomotul, dependent si el de lungimea liniei. In plus, semnalul de date insusi este distorsionat datorita caracteristicilor electrice ale mediului de transmisiune. Distanta de transmisiune poate fi marita prin utilizarea repetoarelor regeneratoare.
Este necesara totusi o anumita codare de linie pentru a asigura semnalului transmis o serie de caracteristici, dupa cum urmeaza:
sa nu aiba componenta de curent continuu si nici componente importante la frecvente foarte joase, deoarece echipamentul de transmisiune se cupleaza la linie prin transformatoare si acestea introduc o atenuare mare la frecvente joase;
sa prezinte un spectru de frecvente cat mai ingust din punct de vedere practic pentru a utiliza cat mai eficient banda de frecevente a liniei de transmisiune si pentru a evita zona de frecvente inalte in care atenuarea liniei este foarte mare;
sa prezinte o protectie cat mai buna fata de zgomot;
sa fie prezenta informatia de timp (tranzitii), necesara pentru sincronizarea bazei de timp a receptorului, indiferent de structura secventei de date;
sa nu necesite la receptie determinarea polaritatii absolute a semnalului sau, alfel spus, in cazul reprezentarii datelor in dubla polaritate, inversarea firelor liniei de transmisiune sa nu aiba efect asupra datelor reconstituite la receptie.
Facand o comparatie intre reprezentarea datelor in simpla polaritate si in dubla polaritate trebuie mentionat ca pentru transmiterea in linie este de preferat reprezentarea in dubla polaritate, deoarece aceasta asigura o protectie mai buna fata de zgomotul aditiv provenit din linia de transmisiune, la aceeasi tensiune maxima admisa pe linie si corectitudinea datelor reconstituite la receptie este mai putin afectata de variatia nivelului semnalului receptionat decat in cazul reprezentarii in simpla polaritate.
Exista un mare numar de reprezentari ale datelor (coduri de linie), fiecare corespunzand numai partial dezideratelor mentionate mai sus. In figura 1.1 sunt prezentate cateva dintre aceste reprezentari electrice ale datelor (semnale de date in banda de baza).
Cea mai utilizata metoda pentru a reprezenta o secventa binara foloseste semnalul binar fara intoarcere la zero (NRZ - Non Return to Zero, figura 1.1.a). Acest semnal nu este recomandat pentru transmiterea directa pe o linie de transmisiune in banda de baza pentru ca atenuarea foarte mare introdusa de transformatoarele de linie pentru componentele foarte importante, de frecventa joasa, ale semnalului, va determina deformarea sa intr-o asemenea masura incat nu va mai fi posibila reconstituirea fara erori a datelor la receptie. In plus, pentru un sir lung de simboluri de acelasi tip nu vor fi tranzitii in semnalul de date, ceea ce inseamna ca va lipsi informatia de timp necesara pentru sincronizarea bazei de timp a receptorului.
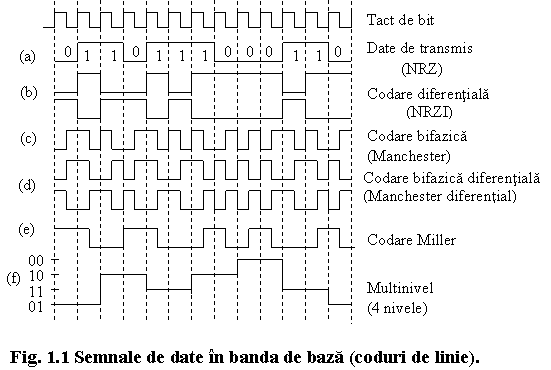
Pentru a nu avea componente importante la frecvente joase se poate folosi codarea bifazica, numita si Manchester (figura 1.1.c). Semnalul bifazic se obtine reprezentand simbolul 1 prin chiar tactul de bit iar simbolul 0 prin tactul de bit inversat. Semnalul bifazic prezinta tranzitii indiferent de structura secventei de date.
Pentru a evita necesitatea determinarii polaritatii absolute a semnalului la receptie, atunci cand datele sunt reprezentate in dubla polaritate, se foloseste codarea diferentiala, prin tranzitii, numita si codare fara intoarcere la zero, inversat (NRZI - Non Return to Zero Inverted, figura 1.1.b). Simbolului 1 ii va corespunde o tranzitie in semnal la inceputul intervalului de simbol iar pentru simbolul 0 nu va fi tranzitie. Altfel spus, simbolul 0 se reprezinta ca si simbolul anterior, indiferent de natura acestuia, iar simbolul 1 se reprezinta in mod diferit de simbolul anterior.
Folosind simultan codarea diferentiala si codarea bifazica rezulta codul bifazic diferential (Manchester diferential, figura 1.1.d). Elementele de semnal utilizate sunt cele de la codarea bifazica, dar fara a avea o asociere fixa cu simbolurile 0 si 1: simbolul 0 se reprezinta prin acelasi element de semnal ca si simbolul anterior, indiferent de natura acestuia, simbolul 1 se reprezinta in mod diferit de simbolul anterior (prin celalalt element de semnal).
Codarea Miller se obtine din codarea bifazica diferentiala prin suprimarea unei tranzitii din doua (figura 1.1.e). Altfel spus, semnalul in cod Miller prezinta tranzitii numai la tranzitiile de un anume sens din semnalul bifazic diferential. Acest cod prezinta avantajul unui spectru de frecvente mai concentrat, cu o pondere a componentelor de joasa frecventa depinzand de frecventa tactului de bit.
Reprezentarea multinivel utilizeaza un numar M de nivele care este, de regula, o putere a lui 2, M = 2m, fiecarui nivel corespunzandu-i un grup de m biti (figura 1.1.f, pentru M = 4). Aceasta reprezentare are avantajul unui spectru mai ingust, dar protectia fata de zgomot este mai mica din cauza distantei mai mici dintre nivelele semnalului (la o aceeasi putere medie a semnalului).
Dupa cum se poate constata, fiecare reprezentare are avantaje dar si dezavantaje, astfel ca alegerea unei anumite reprezentari va fi determinata de tipul aplicatiei.
Densitatea spectrala de putere a acestor semnale este prezentata in figura 1.2.
![]()
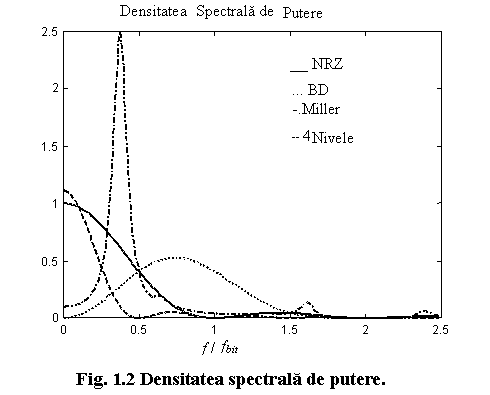
Se poate demonstra ca functiile de densitate spectrala de putere pentru cateva dintre cele mai utilizate semnale de date in banda de baza (considerate semnale aleatoare) sunt exprimate prin urmatoarele formule:
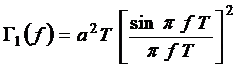 (NRZ, NRZI) (1.1)
(NRZ, NRZI) (1.1)
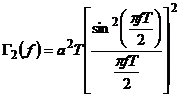 (Manchester, Manchester Diferential) (1.2)
(Manchester, Manchester Diferential) (1.2)
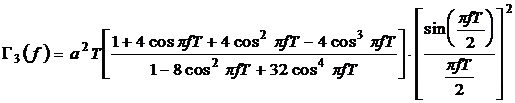 (Miller)(1.3)
(Miller)(1.3)
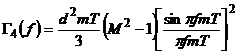 (multinivel)(1.4)
(multinivel)(1.4)
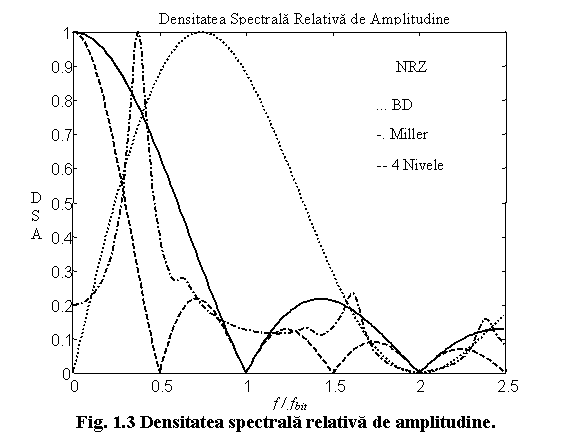
In practica este mult mai convenabil sa se lucreze cu densitatea spectrala relativa de amplitudine:
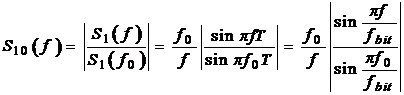 (1.5)
(1.5)
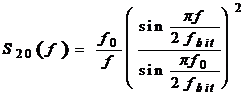 (1.6)
(1.6)
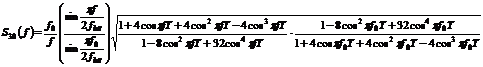 (1.7)
(1.7)
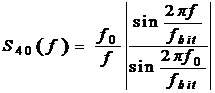 (1.8)
(1.8)
unde 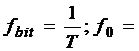 o frecventa de referinta. Densitatile spectrale
relative de amplitudine pentru expresiile de mai sus sunt reprezentate in
figura figura 1.3.
o frecventa de referinta. Densitatile spectrale
relative de amplitudine pentru expresiile de mai sus sunt reprezentate in
figura figura 1.3.
1.2 Utilizarea MATLAB si SIMULINK pentru ANALIZA SPECTRALA A SEMNALELOR DE DATE in banda de baza
1.2.1 Prezentare generala
In continuare vor fi prezentate modelele SIMULINK pentru generatoarele codurilor de linie NRZ, NRZI, Manchester, Manchester diferential, Miller si 4-Nivele. Aceste modele vor fi utilizate pentru a genera semnalele si apoi spectrele lor vor fi analizate cu ajutorul aceleiasi functii MATLAB ca si in lucrarea precedenta, functie ce poarta numele calcul_fft. Aceasta functie estimeaza componentele spectrului de amplitudine pentru un vector de esantioane in domeniu timp dat si pentru o anumita frecventa de esantionare. Functia returneaza doi vectori: unul cu valorile amplitudinilor din domeniul frecventa, rezultate in urma unor prelucrari efectuate la frecventele din al doilea vector.
1.2.2 Generatorul de semnal NRZ
Deschideti SIMULINK si apoi modelul nrz.mdl de la urmatoarea locatie: C:Student. Schema bloc a generatorului de semnal NRZ va fi afisata in SIMULINK, ca in figura 1.4.
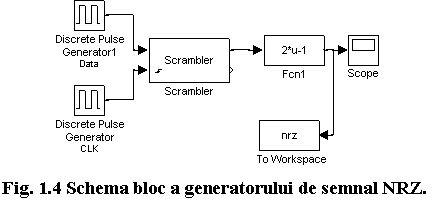
Primul bloc "Discrete Pulse
Generator" (cel de deasupra) furnizeaza un semnal de date 1:7 periodic, cu
o frecventa de bit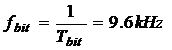 In consecinta,
parametrii acestui bloc vor avea urmatoarele valori: amplitude = 1, period
= 8 samples, pulse width = 1 sample, phase delay = 0 samples, si sample
time = 1/9600. Cel de-al doilea bloc "Discrete Pulse Generator" genereaza
un semnal de tact 1:1 cu frecventa = 9600Hz, utilizat in procesul de
aleatorizare. Parametrii acestui bloc vor avea urmatoarele valori:
amplitude = 1, period = 2 samples, pulse width = 1 sample, phase delay = 0
samples, si sample time = 1/19200. Blocul "Scrambler" mareste perioada
semnalului de date 1:7 de la intrare de N
= 127 de ori. De fapt, scrambler-ul este un registru de deplasare cu
reactie al carui polinom generator este
In consecinta,
parametrii acestui bloc vor avea urmatoarele valori: amplitude = 1, period
= 8 samples, pulse width = 1 sample, phase delay = 0 samples, si sample
time = 1/9600. Cel de-al doilea bloc "Discrete Pulse Generator" genereaza
un semnal de tact 1:1 cu frecventa = 9600Hz, utilizat in procesul de
aleatorizare. Parametrii acestui bloc vor avea urmatoarele valori:
amplitude = 1, period = 2 samples, pulse width = 1 sample, phase delay = 0
samples, si sample time = 1/19200. Blocul "Scrambler" mareste perioada
semnalului de date 1:7 de la intrare de N
= 127 de ori. De fapt, scrambler-ul este un registru de deplasare cu
reactie al carui polinom generator este ![]() (polinom primitiv); fiecare stare a
registrului este determinata de 7 biti si de aceea perioada
semnalului se mareste de
(polinom primitiv); fiecare stare a
registrului este determinata de 7 biti si de aceea perioada
semnalului se mareste de ![]() de ori. Parametrii blocului
"Scrambler' vor fi urmatorii: calculation base = 2, scramble
polynomial = [0 -1 -7], si initial state = [1 1 1 1 1 1 1]. De aceea,
secventa de date la iesirea scrambler-ului este inca o
secventa periodica, avand insa o perioada
foarte mare TNRZ = 127*8*Tbit = 1016*Tbit = 1016/9600 s =
0.10583333333333 s. Semnalele periodice a caror perioada este foarte mare poarta numele de semnale
pseudoaleatoare. Un semnal cu adevarat aleator are o
perioada care tinde la infinit. Deci, cu cat este mai mare perioada
semnalului, cu atat semnalul respectiv se apropie mai mult de unul cu
adevarat aleator. Blocul functional Fcn este utilizat pentru a
transforma secventa binara (1/0) intr-un semnal cu dubla
polaritate (+1/-1) care va fi de fapt chiar secventa NRZ analizata.
Blocul "To Workspace" salveaza iesirea codorului NRZ sub forma unui
vector (sir de esantioane luate din semnal, la momentele de
esantionare) in spatiul de lucru. Pentru acest bloc se vor fixa
urmatorii parametrii: variable name = nrz, sample time = 1/96000, and Save
format = matrix. In urma simularii, in spatiul de lucru MATLAB va fi disponibila
o variabila sir cu numele nrz.
de ori. Parametrii blocului
"Scrambler' vor fi urmatorii: calculation base = 2, scramble
polynomial = [0 -1 -7], si initial state = [1 1 1 1 1 1 1]. De aceea,
secventa de date la iesirea scrambler-ului este inca o
secventa periodica, avand insa o perioada
foarte mare TNRZ = 127*8*Tbit = 1016*Tbit = 1016/9600 s =
0.10583333333333 s. Semnalele periodice a caror perioada este foarte mare poarta numele de semnale
pseudoaleatoare. Un semnal cu adevarat aleator are o
perioada care tinde la infinit. Deci, cu cat este mai mare perioada
semnalului, cu atat semnalul respectiv se apropie mai mult de unul cu
adevarat aleator. Blocul functional Fcn este utilizat pentru a
transforma secventa binara (1/0) intr-un semnal cu dubla
polaritate (+1/-1) care va fi de fapt chiar secventa NRZ analizata.
Blocul "To Workspace" salveaza iesirea codorului NRZ sub forma unui
vector (sir de esantioane luate din semnal, la momentele de
esantionare) in spatiul de lucru. Pentru acest bloc se vor fixa
urmatorii parametrii: variable name = nrz, sample time = 1/96000, and Save
format = matrix. In urma simularii, in spatiul de lucru MATLAB va fi disponibila
o variabila sir cu numele nrz.
Valoarea Stop time pentru aceasta simulare este egala cu perioada semnalului NRZ, cu exceptia ultimului esantion, adica 1016/9600 s - 1/96000 s = 10159/96000 s 1.058229166666667e-001 s. Ultimul esantion nu se ia in calcul deoarece procesul de esantionare incepe la momentul t0 = 0; deci, utilizand o frecventa de esantionare de 10 ori mai mare decat frecventa de bit vor rezulta 10161 esantioane, primul si ultimul fiind identice. Din acest motiv ultimul esantion va trebui eliminat.
Ruland simularea pentru acesti parametrii, ecranul osciloscopului va afisa o perioada a semnalului NRZ esantionat.
Pentru analiza in domeniul frecventa a unui semnal periodic se va utiliza functia MATLAB numita calcul_fft. Aceasta functie estimeaza amplitudinea componentelor spectrale pentru un anumit vector in domeniul timp si pentru o frecventa de esantionare specificata. Functia intoarce doi vectori: unul cu valorile amplitudinilor in domeniul frecventa rezultate in urma prelucrarilor facute la frecventele din cel de-al doilea vector.
Considerand parametri de mai sus, se va determina spectrul de amplitudini al semnalului NRZ dat de vectorul nrz. Apelati functia calcul_fft cu urmatoarea comanda:
>>[f,A]=calcul_fft(nrz,96000);
Frecventa de esantionare este 96000Hz, aceeasi cu frecventa de esantionare utilizata pentru variabila nrz in blocul "To Workspace". A este vectorul ale carui elemente sunt valorile amplitudinilor, iar vectorul f contine valorile frecventelor. Acesti doi vectori au aceeasi lungime.
Se va utiliza functia stem pentru afisarea spectrului de amplitudini al vectorului nrz, reprezentand A ca functie de vectorul f:
>>stem(f,A)
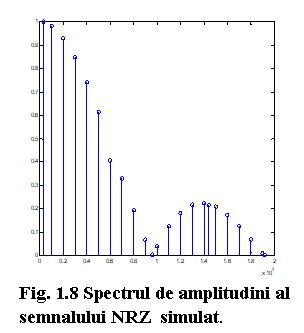
Imaginea care rezulta este ilustrata in figura 1.5.
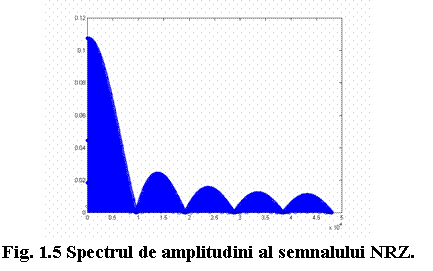
Observati ca spectrul de amplitudini al semnalului NRZ este inca un spectru discret (deoarece un semnal aleatoriu ar trebui sa aiba un spectru continuu), avand componente la multipli de frecventa de repetitie a semnalului (in acest caz particular, la multipli de 9600/1016Hz ). De asemenea, remarcati faptul ca anvelopa semnalului se anuleaza la multipli frecventei de bit (in acest caz la multipli de 9600Hz). Deci, semnalul va avea 1016 componente in fiecare lob.


Analiza spectrala a semnalului
de date se realizeaza cu ajutorul unui voltmetru selectiv. Acesta se
utilizeaza pentru a masura valoarea efectiva a amplitudinii
componentelor unui semnal. Un voltmetru selectiv este format, in principal,
dintr-un filtru trece banda care permite trecerea componentelor din banda
sa de trecere, de largime B, si taie celelalte componente. Caracteristica
reala a unui asemenea filtru este ilustrata in figura 1.6.
Masurarea corecta a amplitudinii unei componente se face atunci cand frecventa ei este egala cu frecventa centrala a filtrului fc . Daca aceste doua frecvente nu sunt egale, componenta va fi atenuata cu atat mai mult cu cat diferenta f-fc este mai mare. In figura 1.7 amplitudinea componentei masurate f va de doua ori mai mica decat in cazul f=fc.
Pentru a implementa un voltmetru selectiv, in MATLAB a fost creata o functie cu numele voltm_sel. Aceasta functie implementeaza un filtru trece banda Nyquist cu banda efectiva (banda la 3dB) egala cu 100Hz, centrata pe frecventa fc. Componentele filtrate, care sunt in banda de trecere a filtrului, sunt utilizate pentru a estima tensiunea efectiva cu formula:
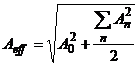 (1.9)
(1.9)
unde A0 este componenta de curent continuu (care este in banda de trecere doar pentru fc = 0Hz ) iar An sunt armonicele filtrate.
Functia voltm_sel estimeaza valorile efective ale tensiunii pentru un anumit vector din domeniul frecventa si o frecventa centrala a filtrului trece banda fc specificata. Functia intoarce o valoare scalara care este valoarea efectiva a tensiunii estimata cu formula (1.9). Considerand diferite valori pentru frecventa centrala, se pot masura valorile efective ale spectrului de amplitudini pentru semnalul NRZ.
Se vor determina tensiunile efective ale spectrului semnalului NRZ date de vectorul A la frecventa 0.3KHz. Apelati functia voltm_sel cu urmatoarea comanda:
>>Aef=voltm_sel(A,300)
In MATLAB va fi afisata valoarea estimata (in volti) a tensiunii efective la 0.3KHz.
Aef =
1.470269228974444e-001
Considerati acele valori ale frecventei astfel incat sa selectati cele mai importante regiuni din spectrul de amplitudini al semnalului NRZ prezentat in figura 1.5. In acest spectru, selectati limitele maxima si minima pentru fiecare lob. De exemplu, la frecventa de 9600Hz in spectrul de amplitudini se gaseste o valoare minima. Pentru a obtine un grafic mai detaliat considerati, in continuare, cateva valori intermediare ale frecventei.
Raportul Aef(f)/Aef(f0) se va determina la diferite frecvente, f0 fiind o frecventa de referinta, dupa care se va compara cu valorile teoretice S(f)/S(f0).
Aef(f) se va determina
intr-o gama de frecvente intre 0 si 2fbit. Se va alege apoi o frecventa de
referinta f0 corespunzatoare (de
preferinta la o valoare maxima a Aef(f) si intr-o zona in care Aef(f) nu variaza prea
mult) si se va calcula raportul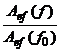
De exemplu, se considera urmatoarele valori ale frecventei: fI Hz.
Pentru a determina valorile simulate Aef(f) se utilizeaza fereastra de comenzi MATLAB si se apeleaza functia voltm_sel pentru urmatoarele valori ale frecventei:
>>Asim=[voltm_sel(A,300) voltm_sel(A,1000) voltm_sel(A,2000) voltm_sel(A,3000) voltm_sel(A,4000) +
voltm_sel(A,5000) voltm_sel(A,6000) voltm_sel(A,7000) voltm_sel(A,8000) voltm_sel(A,9000) +
voltm_sel(A,9600) voltm_sel(A,10000) voltm_sel(A,11000) voltm_sel(A,12000) voltm_sel(A,13000) +
voltm_sel(A,14000) voltm_sel(A,14400) voltm_sel(A,15000) voltm_sel(A,16000) voltm_sel(A,17000) +
voltm_sel(A,18000) voltm_sel(A,19000) voltm_sel(A,19200)];
Pentru a obtine valorile relative 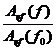 , se vor imparti elementele vectorului Asim la valoarea
maxima din acest vector (care este tensiunea efectiva la
frecventa f0 = 300 Hz ).
, se vor imparti elementele vectorului Asim la valoarea
maxima din acest vector (care este tensiunea efectiva la
frecventa f0 = 300 Hz ).
>>Arel=Asim/max(Asim);
Valorile teoretice S(f)/S(f0)
sunt calculate cu formula (1.5), pentru aceleasi valori ale
frecventei utilizate la determinarea valorilor simulate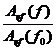 . Utilizati MATLAB pentru a specifica acest set de
valori ale frecventei:
. Utilizati MATLAB pentru a specifica acest set de
valori ale frecventei:
>>f1=[0.3 1 2 3 4 5 6 7 8 9 9.6 10 11 12 13 14 14.4 15 16 17 18 19 19.2]*1000;
Se poate utiliza fereastra de comenzi MATLAB pentru a determina valorile teoretice S(f)/S(f0) cu urmatoarea comanda:
>> S10=abs(sinc(f1/9600)/sinc(300/9600));
unde fbit = 9600Hz si frecventa de referinta f0 = 300Hz.
Pentru a compara spectrul de amplitudini rezultat in urma simularii cu cel teoretic utilizati urmatoarele comenzi:
>>figure(1);stem(f1,Arel)
>>figure(2);stem(f1,S10)
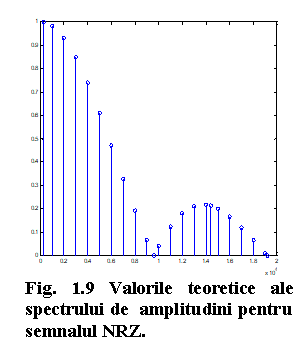
Vor fi afisate urmatoarele
figuri:
Deschideti modelul bifazic_dif.mdl de la urmatoarea locatie: C:Student. SIMULINK va afisa schema bloc a generatorului de semnal Manchester diferential, ca in figura 1.10.
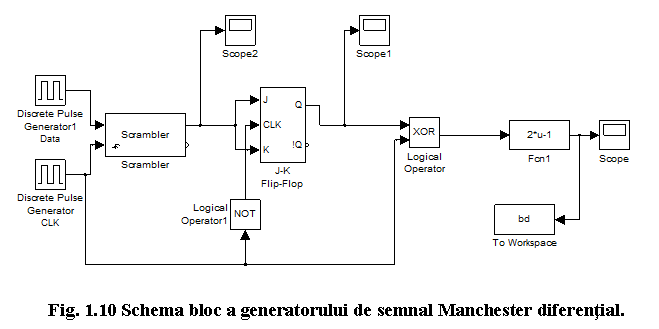
Aceasta schema include blocurile de generare a semnalului NRZ, deoarece se genereaza semnalul Manchester direfential plecand de la cel NRZ. Deci, la intrarile J si K ale bistabilului J-K avem acelasi semnal de la generatorul NRZ, adica secventa binara NRZ (elemente 0/1).
Bistabilul J-K realizeaza o codare diferentiala, deci la iesirea lui vom avea un semnal NRZI. Blocul XOR realizeaza operatia logica de adunare a tactului cu semnalul NRZI.
Blocul functional Fcn este utilizat pentru a converti secventa binara (1/0) intr-un semnal cu dubla polaritate, care va fi de fapt semnalul Manchester diferential analizat. Blocul "To Workspace" salveaza iesirea blocului Manchester diferential sub forma unui vector in spatiul de lucru (sir de esantioane luate din semnal la momentele de esantionare). Pentru acest bloc se vor fixa urmatorii parametrii: variable name = bd, sample time = 1/96000, si Save format = matrix. In urma simularii, in spatiul de lucru MATLAB va fi disponibila o variabila sir cu numele bd.
Valoarea Stop Time pentru aceasta simulare este egala cu perioada semnalului Manchester diferential, cu exceptia ultimului esantion, adica 1016/9600 s - 1/96000 s = 10159/96000 s 1.058229166666667e-001 s. Ultimul esantion nu este luat in calcul deoarece procesul de esantionare incepe la momentul t0=0; deci, utilizand o frecventa de esantionare de 10 ori mai mare decat frecventa de bit vor rezulta 10161 de esantioane, primul si ultimul fiind identice. Din acest motiv ultimul esantion trebuie eliminat.
Ruland simularea pentru acesti parametri, ecranul osciloscopului va afisa o perioada a semnalului Manchester diferential esantionat.
Utilizati functia MATLAB numita calcul_fft pentru analiza spectrului de amplitudini al acestui semnal.
Graficul care rezulta este prezentat in figura 1.11.
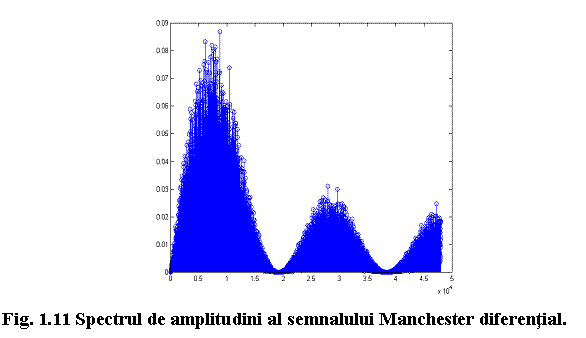
Observati faptul ca spectrul de amplitudini al semnalului Manchester diferential este inca un spectru discret (deoarece un semnal cu adevarat aleator ar trebui sa aiba un spectru continuu), avand componente spectrale nenule doar la multiplii frecventei semnalului (in acest caz particular la multipli de 9600/1016Hz). Remarcati, de asemenea faptul ca anvelopa se anuleaza la multiplii dublului frecventei de bit (in acest caz, la multipli de 19200Hz). Deci, exista 2032 componente in fiecare lob.
Utilizati functia MATLAB care implementeaza voltmetru selectiv, voltm_sel, si determinati tensiunile efective pentru spectrul de amplitudini al semnalului Manchester diferential, la diverse valori ale frecventei.
Considerati acele valori pentru frecventa centrala fc, astfel incat sa selectati cele mai importante regiuni in spectrul semnalului Manchester diferential prezentat in figura 1.11. Selectati limitele minima si maxima pentru fiecare lob. Pentru a obtine un grafic mai detaliat, luati in consideratie valori intermediare ale frecventei.
Raportul Aef(f)/Aef(f0) va fi determinat la diferite frecvente, f0 fiind frecventa de referinta; comparati apoi valorile obtinute cu cele teoretice S(f)/S(f0).
Valoarea Aef(f) va fi determinata
in gama de frecvente intre 0 si 2fbit.
Se va alege apoi o frecventa de referinta f0 (de preferinta
unde Aef(f) are valoarea
maxima si nu variaza prea mult), dupa care
se calculeaza raportul 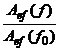
Valorile teoretice S(f)/S(f0) sunt calculate cu formula (1.6) pentru
aceleasi valori ale frecventei utilizate la determinarea valorilor
simulate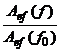
Puteti utiliza fereastra de comenzi MATLAB pentru a determina valorile teoretice S(f)/S(f0), cu urmatoarea comanda:
>>S20=f1/f0.*((sinc(f1/(2*9600))/sinc(f0/(2*9600))).^2);
unde fbit = 9600Hz, si frecventa de referinta f0 se alege ca mai sus.
Pentru a compara spectrul de amplitudini rezultat in urma simularii cu cel teoretic utilizati urmatoarele comenzi:
>>figure(1);stem(f1,Arel)
>>figure(2);stem(f1,S20)
1.2.4 Generatorul de semnal Miller
Deschideti modelul miller.mdl de la urmatoarea locatie: C:Student. Simulink va afisa schema bloc a generatorului de semnal Miller, ca in figura 1.12.
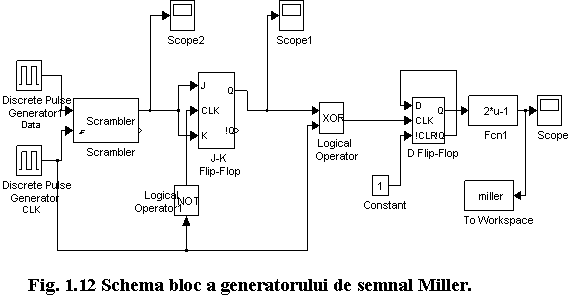
Schema bloc prezentata in figura 1.12 este identica cu cea a generatorului de semnal Manchester diferential prezentat in figura 1.10, pana la iesirea blocului XOR. Deci, la intrarile J si K ale bistabilului J-K avem acelasi semnal de la iesirea generatorului NRZ, adica chiar secventa binara NRZ (elemente 1/0). Bistabilul J-K realizeaza o codare diferentiala, astfel incat la iesirea lui vom avea un semnal NRZI. Blocul XOR realizeaza operatia logica de adunare a tactului cu semnalul NRZI. Pe intrarea de ceas a bistabilului D avem acelasi semnal de la iesirea generatorului Manchester diferential, adica secventa binara (elemente 0/1) Manchester diferential.
Bistabilul D realizeaza o codare Miller prin suprimarea unei tranzitii din doua in semnalul de date Manchester diferential. Rolul blocului functional Fcn este de a converti secventa binara (1/0) intr-un semnal cu dubla polaritate (+1/-1). De fapt, aceasta va fi chiar secventa de date Miller analizata.
Blocul "To Workspace" salveaza iesirea codorului Miller sub forma unui vector (sir de esantioane luate din semnal la momentele de esantionare) in spatiul de lucru. Pentru acest bloc vor fi setati urmatorii parametrii: variable name = miller, sample time = 1/96000, si Save format = matrix. In urma simularii, in spatiul de lucru MATLAB va fi disponibila o variabila sir cu numele miller.
Valoarea Stop time pentru aceasta simulare este egala cu perioada semnalului Miller, exceptie facand ultimul esantion, adica 1016/9600 s - 1/96000 s = 10159/96000 s 1.058229166666667e-001 s. Ultimul esantion nu se ia in calcul deoarece procesul de esantionare incepe la momentul t0=0. Deci, utilizand o frecventa de esantionare de 10 ori mai mare decat frecventa de bit vor rezulta 10161 esantioane, primul si ultimul fiind identice. Din acest motiv ultimul esantion va fi eliminat.
Ruland simularea pentru acesti parametri, ecranul osciloscopului va afisa o perioada a semnalului Miller esantionat.
Pentru a analiza spectrul de amplitudini al semnalului codat Miller se va apela functia MATLAB numita calcul_fft.
Rezultatul este ilustrat in figura 1.13:
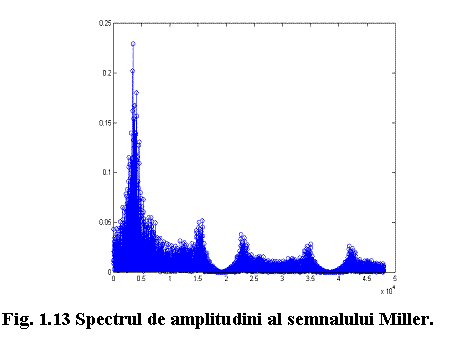
Remarcati faptul ca spectrul de amplitudini al semnalului Miller este inca un spectru discret (un semnal cu adevarat aleator are un spectru continuu), avand toate componentele la multipli frecventei semnalului (in acest caz, la multipli de 9600/1016Hz). Observati, de asemenea, ca anvelopa semnalului se anuleaza la frecvente egale cu multipli de 2fbit (in acest caz la multipli de 19200Hz). Deci, semnalul va avea 2032 de componente in fiecare lob.
Utilizati functia MATLAB care implementeaza voltmetru selectiv, voltm_sel, si determinati tensiunile efective pentru spectrul de amplitudini al semnalului Miller, la diverse valori ale frecventei.
Considerati acele valori pentru frecventa centrala fc, astfel incat sa selectati cele mai importante regiuni in spectrul semnalului Miller prezentat in figura 1.13; selectati limitele minima si maxima pentru fiecare lob. Pentru a obtine un grafic mai detaliat, luati in calcul valori intermediare ale frecventei.
Raportul Aef(f)/Aef(f0) va fi determinat la diferite frecvente, f0 fiind frecventa de referinta; comparati apoi valorile obtinute cu cele teoretice S(f)/S(f0).
Valoarea Aef(f)
va fi determinata in gama de frecvente intre 0 si 2fbit. Se va alege apoi o
frecventa de referinta f0
(de preferinta unde Aef(f)
are valoarea maxima si nu variaza prea mult), dupa care
se calculeaza raportul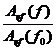
Valorile teoretice S(f)/S(f0) sunt calculate cu formula (1.7) pentru
aceleasi valori ale frecventei, utilizate la determinarea valorilor
simulate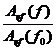
Puteti utiliza fereastra de comenzi MATLAB pentru a determina valorile teoretice S(f)/S(f0), cu urmatoarea comanda:
>>S30=abs((sinc(f1/(2*9600))/sinc(f0/(2*9600))).*
sqrt((1+4*cos(pi*f1/9600)+4*(cos(pi*f1/9600)).^2-4*(cos(pi*f1/9600)).^3)./
(1-8*(cos(pi*f1/9600)).^2+32*(cos(pi*f1/9600)).^4)*(1-8*cos(pi* f0/9600)^2+
32*cos(pi*f0/9600)^4)./(1+4*cos(pi* f0/9600)+4*cos(pi* f0/9600)^2-
4*cos(pi* f0/9600)^3)));
unde fbit = 9600Hz, si frecventa de referinta f0 se alege ca mai sus.
Pentru a compara spectrul de amplitudini rezultat in urma simularii cu cel teoretic utilizati urmatoarele comenzi:
>>figure(1);stem(f1,Arel)
>>figure(2);stem(f1,S30)
1.2.5 Generatorul de semnal 4-Nivele
Deschideti modelul fourlevels.mdl de la urmatoarea locatie: C:Student . SIMULINK va afisa schema bloc a generatorului de semnal 4-Nivele, ca in figura 1.14.
Schema bloc prezentata in figura 1.14 este identica cu cea a generatorului de semnal NRZ din figura 1.4 pana la intrarea blocului de intarziere si a bistabilului D 3 (D Flip-Flop3). Deci, la intrarea bistabilului D Flip-Flop3 avem un semnal NRZ (elemente binare 1/0).
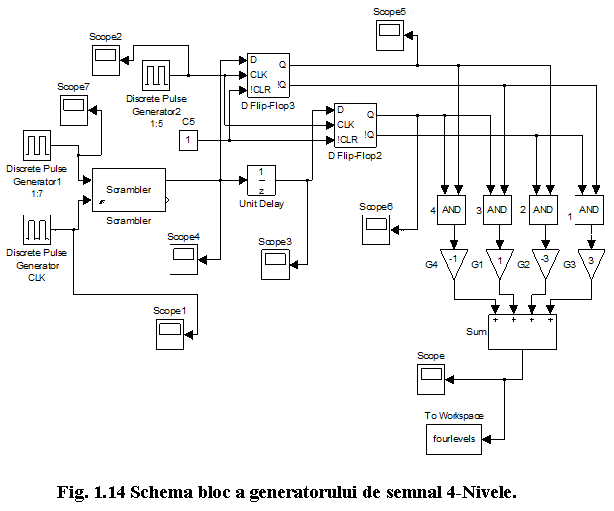
Blocurile
"Discrete Pulse Generator2", "Unit Delay, "D Flip-Flop2" si "D Flip-Flop3"
sunt utilizate pentru a imparti sirul de biti ce
reprezinta semnalul NRZ in doua siruri paralele. Bitii de ordin impar din sirul
NRZ sunt plasati la iesirea blocului "D Flip-Flop2", iar cei de ordin
par la iesirea blocului "D Flip-Flop3". Fiecare din perechile de biti
paraleli este utilizata pentru a selecta unul din cele 4 nivele: -3V, -1V,
+1V, +3V la iesirea codorului 4-Nivele (conform regulii de codare
prezentata mai sus). Aceasta selectie se realizeaza cu
ajutorul celor patru blocuri AND, a celor patru blocuri amplificatoare (fiecare
cu un castig diferit) si a sumatorului (SUM) cu patru intrari.
La iesirea blocului sumator vom avea un semnal 4-Nivele.
Blocul "To Workspace" salveaza iesirea codorului 4-Nivele sub forma unui vector (sir de esantioane luate din semnal la momentele de esantionare) in spatiul de lucru. Pentru acest bloc vor fi setati urmatorii parametrii: variable name = fourlevels, sample time = 1/96000, si Save format = matrix. In urma simularii, in spatiul de lucru MATLAB va fi disponibila o variabila sir cu numele fourlevels.
Aceasta schema introduce o intarziere (intre generarea semnalului NRZ si generarea semnalului 4-Nivele) de un interval de bit (1/9600s). Deci, luand o frecventa de esantionare de 10 ori mai mare decat frecventa de bit, semnalul va avea o intarziere de 10 esantioane.
Valoarea Stop time pentru aceasta simulare este egala cu perioada semnalului 4-Nivele plus un interval de bit (datorita intarzierii), exceptand ultimul esantion, adica 1016/9600 s + 10/96000 - 1/96000 s= 10169/96000 s 1.059270833333333e-001 s. Ultimul esantion nu se ia in calcul deoarece procesul de esantionare incepe la momentul t0=0; deci, utilizand o frecventa de esantionare de 10 ori mai mare decat frecventa de bit vor rezulta 10171 esantioane, primul si ultimul fiind identice. Din acest motiv ultimul esantion va fi eliminat.
Ruland simularea pentru acesti parametri, ecranul osciloscopului va afisa o perioada a semnalului 4-Nivele esantionat plus 10 esantioane de intarziere.
Eliminati primele 10 esantioane (datorate intarzierii) cu urmatoarea comanda:
>>fourlevels1= fourlevels(11:10170);
Variabila fourlevels1 selecteaza o perioada a semnalului 4-Nivele esantionat.
Utilizati functia MATLAB
numita calcul_fft pentru a analiza spectrul de amplitudini al semnalului
4-Nivele (pentru variabila fourlevels1)
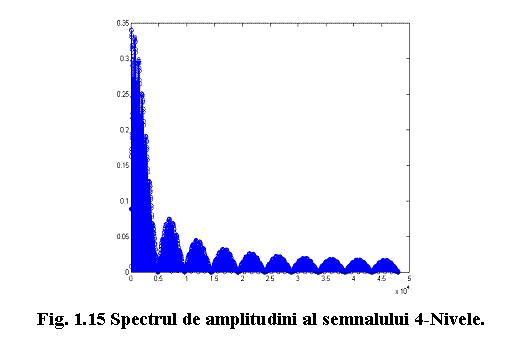
Imaginea care rezulta este prezentata in figura 1.15.
Remarcati faptul ca spectrul de amplitudini al semnalului 4-Nivele este inca un spectru discret (un semnal cu adevarat aleator are un spectru continuu), avand toate componentele la multipli frecventei semnalului (in acest caz, la multipli de 9600/1016Hz). Observati, de asemenea, ca anvelopa semnalului se anuleaza la frecvente egale cu multiplii de fbit /2 (in acest caz la multiplii de 4800Hz). Deci, semnalul va avea 508 componente in fiecare lob.
Utilizati functia MATLAB care implementeaza voltmetru selectiv, voltm_sel, si determinati tensiunile efective pentru spectru de amplitudini al semnalului 4-Nivele, la diverse valori ale frecventei.
Considerati acele valori pentru frecventa centrala fc, astfel incat sa selectati cele mai importante regiuni in spectrul semnalului 4-Nivele prezentat in figura 1.15; selectati limitele minima si maxima pentru fiecare lob. Pentru a obtine un grafic mai detaliat, luati in calcul valori intermediare ale frecventei.
Raportul Aef(f)/Aef(f0) va fi determinat la diferite frecvente, f0 fiind frecventa de referinta; comparati apoi valorile obtinute cu cele teoretice S(f)/S(f0).
Valoarea Aef(f)
va fi determinata in gama de frecvente intre 0 si 2fbit. Se va alege apoi o
frecventa de referinta f0
(de preferinta unde Aef(f)
are valoarea maxima si nu variaza prea mult), dupa care
se calculeaza raportul 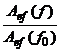
Valorile teoretice S(f)/S(f0) sunt calculate cu formula (1.8) pentru
aceleasi valori ale frecventei, utilizate la determinarea valorilor
simulate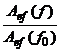
Puteti utiliza fereastra de comenzi MATLAB pentru a determina valorile teoretice S(f)/S(f0), cu urmatoarea comanda:
>>S40=abs(sinc(2*f1/9600)/sinc(2*f0/9600));
unde fbit = 9600Hz, si frecventa de referinta f0 se alege ca mai sus.
Pentru a compara spectrul de amplitudini rezultat in urma simularii cu cel teoretic utilizati urmatoarele comenzi:
>>figure(1);stem(f1,Arel)
>>figure(2);stem(f1,S40)
1. De ce este preferata determinarea rapoartelor S(f)/S(f0) sau Aef(f)/Aef(f0) si nu a valorilor S(f) sau Aef(f)?
2. Care sunt avantajele si dezavantajele codului bifazic?
3. Cand se recomanda utilizarea codului Miller?
4. Semnalele analizate sunt, de fapt, semnale periodice. Cate linii spectrale sunt intr-o banda egala cu banda de trecere a filtrului din voltmetrului selectiv?
5. Care sunt principalele cauze ale diferentei dintre rezultatele simulate si valorile teoretice?