|
|
|
Teorema lui Nernst
Ecuatiile de definire a functiilor U, H, S, F, G:
; 
; 
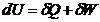; F = U - TS; G = H - TS
arata ca expresiile analitice ale functiilor U, H si S contin o constanta de integrare nedeterminata si deci, F si G contin un termen arbitrar de forma a + bT. In legatura cu aceste observatii se aminteste faptul ca valorile ΔU, ΔH, ΔS, corespunzatoare unor transformari finite in starea sistemului, sunt bine determinate, pe cand valorile corespunzatoare ΔF si ΔG sunt determinate numai in cazul cand ambele stari, initiala si finala, ale transformarii au aceeasi temperatura (v. exemplul XIV.13).
In studiul termodinamic al unui proces, cercetatorul trebuie sa calculeze ΔF sau ΔG, deci caracteristicile starii de echilibru a sistemului. Determinarea experimentala a starii de echilibru permite evaluarea acestor marimi, dar principiul al treilea al termodinamicii permite calculul lor (ΔF si ΔG) a priori, din datele termice (determinate calorimetric) ale sistemului (caldura de transformare si capacitatile calorice ale substantelor din sistem).
Prima forma de enuntare a principiului al treilea (teorema lui Nernst) este legata de calculul constantei de echilibru a unei reactii chimice din date termice.
Din ecuatia Gibbs-Helmholtz (v. ecuatia (XIV.35)):
este evident
ca 
la T = 0, daca 
nu are o valoare
infinita. Observatiile experimentale arata ca, la
scaderea temperaturii scade si 
, si deci apropierea diferentei 
de zero este de un
ordin superior. Teorema enuntata de Nernst se exprima matematic
prin ecuatiile:
(XV.1)
Ecuatiile (XV.1) trebuie limitate la solide.
Exemplul 1. Determinarile experimentale arata ca diferenta tinde catre zero
o data cu scaderea temperaturii. Sa se analizeze posibilitatile
matematice de verificare a conditiei la T = 0.
Rezolvare:
Conditia este verificata
in urmatoarele trei cazuri matematic posibile, caracterizate prin
ecuatiile: a, b, c si reprezentate in (fig. XV.1):
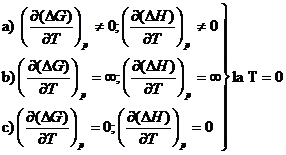
(Fig. XV.1.c) reprezinta teorema lui Nernst.
Oricare din cele doua curbe poate fi ΔG, respectiv ΔH, deoarece
poate fi negativ
sau pozitiv.
Ecuatiile (XV.1) implica si:
(XV.2)
(XV.3)
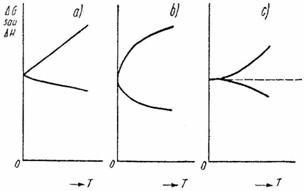
Fig. XV.1. Curbele ΔG si ΔH la 0 oK
Exemplul 2. Sa se arate ca exprimarea matematica a teoremei lui Nernst se poate face numai prin ecuatia (XV.2), necesara si suficienta.
Rezolvare:
Conform ecuatiei Gibbs-Helmholtz (XIV.35) rezulta:
nedeterminare care se ridica prin derivare, deci:
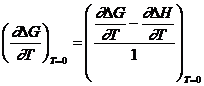
de unde:
(ΔS)T = 0 = (ΔS)T = 0 + (ΔCp)T = 0
si deoarece (ΔS)T = 0 nu este infinit de mare, rezulta:
(ΔCp)T=0 (ecuatia (XV.3))
De asemenea, si ecuatia 
este suficienta pentru a exprima complet teorema lui
Nernst, deoarece cu ecuatia Gibbs-Helmholtz se obtine:
(Sa se arate ca reciproca nu este adevarata).
Din ecuatia (XV.2) rezulta ca variatia de entropie a unei reactii, la temperatura T, poate fi calculata cu ecuatia:
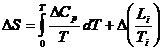(pentru reactia chimica 
)
deoarece constanta de integrare este nula. Li este caldura de transformare (latenta) de faza a substantelor A si B la Ti. Se obtine astfel:
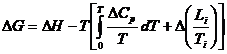
care permite calculul variatiei de entalpie libera din variatii de entalpie si de capacitate calorica a sistemului.
