Tehnici experimentale pentru detectia cuantelor gama cosmice de energie inalta - tehnica Cerenkov

Tehnici experimentale pentru detectia cuantelor gama cosmice de energie inalta - tehnica Cerenkov

Observarea cuantelor gama cosmice se poate face atat de pe sateliti cat si de la sol. Telescoapele montate pe sateliti detecteaza direct cuantele gama ce vin din Univers si le convertesc in perechi electron-pozitron ale caror urme apoi sunt inregistrate. Telescoapele pozitionate la sol detecteaza particulele incarcate secundare si fotonii Cerenkov sau cei proveniti din fluorescenta azotului atmosferic, acestea provenind din cuantele gama cosmice ce au interactionat cu atmosfera. Din cauza fluxurilor scazute pe care le au cuantele gama de energie inalta, 7 10^-15 fotoni m^-2 s^-1 pentru fotoni cu E=400 GeV[1]si a dimensiunilor relativ mici ale telescoapelor ce pot fi plasate pe sateliti, observatiile ce se pot face pe acestia abia ajung la cateva zeci de GeV. Pentru detectia cuantelor gama de energie mare sunt necesare arii de colectare mari si timpi de observare indelungati. Aceste conditii sunt indeplinite de catre telescoapele sau retelele de telescoape Cerenkov sau de catre retelele de detectie a particulelor secundare incarcate. In experimente recente se folosesc sisteme de detectie hibride pentru a imbunatati calitatea inregistrarilor.Ca urmare au fost cuprinsi si detectori de lumina fluorescenta. Cea mai folosita tehnica este cea de detectie a fotonilor Cerenkov,in sensul ca cele mai multe si mai importante descoperiri in domeniul cuantelor gama cosmice de energie mare s-au facut cu aceasta tehnica. Acesta este si motivul pentru care vom acorda un spatiu mai mare de prezentare acestei tehnici.

O clasificare[4] a detectorilor de cuante gama cosmice de energie mare se poate face alegand drept criteriu efectele pe care le produc radiatiile secundare la interactiunea cu substanta. Din acest punct de vedere exista:

a)     spectrometre sau fotometre care contin scintilatori sau detectori solizi care transforma cuantele gama in fotoni optici

b)     detectori de tip "imagistica" care se bazeaza pe producerea de catre cuantele gama de perechi e⁺e^- sau imprastieri Compton pentru a gasi directia de sosire a fotonilor gama; un exemplu de astfel de detector este "masca codata"

O alta clasificare[4] a detectorilor se poate face in functie de mediul in care se produce interactiunea foton gama - atom. Din acest punct de vedere in prezent exista atat detectori cu cristale scintilatoare cat si cu mediu solid (semiconductori).Acestia din urma sunt de germaniu sau din telurid cadmiu zinc ( CdZnTe).Au o rezolutie energetica si spatiala mai buna decat a celor cu cristale scintilatoare si au zgomotul mai mic. In utilizarea lor este insa necesara racirea la temperaturi scazute ceea ce face sa fie mai scumpi decat cei cu scintilatie.Ca si cei cu scintilatie se bazeaza pe ionizarea fotoelectrica a mediului.

Clasificarea pe care o propune Gus Sinnis utilizeaza drept criterii tehnicile experimentale si obiectivele detectiei, rezultand trei categorii :instrumente de mare sensibilitate, instrumente cu energie de prag scazuta si instrumente cu apertura deschisa/ciclu inalt de lucru[2].Primul tip de instrumente realizeaza imagini ale baii de lumina Cerenkov a caror forma si orientare sunt sensibile la directia si tipul radiatiior cosmice primare.Acest tip de detectoare au oglinzi de marime medie.Al doilea tip de detectoare au oglinzi de marimi uriase pentru a putea detecta radiatii cu energii scazute,deci sunt caracterizate de energii de prag coborate(mult sub 100 GeV).Energia de prag a unui telescop cu lumina Cerenkov este invers proportionala cu radacina patrata a ariei oglinzii Desi detectorii celui de-al treilea tip au energii de prag relativ mari ,totusi ei au unele avantaje fata de ceilalti. Pot lucra incontinuu si "vad" intreaga bolta cereasca. S-au facut eforturi de a le micsora energia de prag

1.Tehnica imagistica Cerenkov.Detectori de lumina Cerenkov

Tehnica bazata pe colectarea fotonilor Cerenkov emisi de catre particulele incarcate secundare masoara densitatea laterala a fotonilor,densitate cu ajutorul careia se esti-meaza energia cuantelor gama primare si variabilitatea sursei.

Detectorii de lumina Cerenkov au fost utilizati cu succes in programele Whipple Obser-vatory, CANGAROO I,II si III,CAT,HEGRA in domeniul energetic 300 GeV-10 TeV.

Avantajele pe care le prezinta utilizarea telescoapelor atmosferice Cerenkov(atmospheric Cherenkov telescopes ACT) constau in energia de prag scazuta, rezolutia unghiulara foarte buna si calitatea de a elimina eficient fondul.

Fig.1.1Fotografie a unui telescop de la Whipple Observatory avand o oglinda de 10m diametru (reproducere dupa [12])

Datorita campului mic de vedere telescoapele Cerenkov nu pot insa observa in acelasi timp decat o singura sursa.In plus intrucat sunt instrumente optice ele sunt afectate de conditiile atmosferice. Observatiile facute cu aceste telescoape nu se pot face decat in noptile fara luna si senine.Ca urmare ciclul lor de functionare este de circa 10%[3].

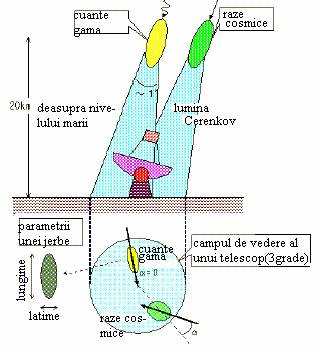
Fig.1.2 Desen reprezentand geometria detectiei jerbelor electromagnetice

Pentru determinarea spectrului in mod adecvat detectorul se foloseste in doua moduri: "on" si "off".In modul "on" detectorul este indreptat catre sursa ce urmeaza a fi observata pentru un interval de timp(de exemplu[7] 28 de minute siderale intr-o serie de experimente in programul Whipple Observatory).(Timpul sideral este timpul masurat prin unghiul orar al punctului vernal). In modul "off" detectorul este indreptat catre o regiune de pe cer lipsita de surse de cuante gama, imaginea fiind a fondului. Tehnicile bazate pe detectia luminii Cerenkov au fost utilizate in programele Whipple Observatory, CAT din Pirineii francezi, HEGRA, CANGAROO, etc.

Tehnica imagistica Cerenkov a jucat un rol foarte important in descoperirea unor surse discrete de cuante gama cu energii de ordinul TeV. Cu aceasta tehnica se pot reda grafic variatiile temporale ale acestor surse, determina pozitiile sursei pe cer si deduce spectrul energetic.In comparatie cu lumina fluorescenta ,pentru o energie primara data, productia luminii Cerenkov este mult mai mare pentru radiatia gama primara decat cea a radiatiilor primare incarcate [2],[7].Exista doua tipuri de tehnici cu lumina Cerenkov:

metoda imagistica; este folosita in programele HEGRA, Whipple ,CANGAROO,CAT

metoda esantionarii frontului de unda(folosita in experimentul HEGRA, acum 5 telescoape cu oglinzi de arie 8,5 m²)

1.1.Echipamente utilizate in tehnica Cerenkov

In aceasta tehnica[8] o oglinda sau un set de oglinzi reflecta lumina Cerenkov catre un set de tuburi fotomultiplicatoare aflat in planul focal al oglinzii; lumina ce vine dintr-o directie este reflectata catre un tub fotomultiplicator iar lumina ce vine dintr-o alta directie este reflectata catre un alt fototub. Astfel se obtine o distributie unghiulara a fotonilor Cerenkov sositi in acelasi loc la sol.

Fiecare tub fotomultiplicator este legat la un amplificator care separa semnalele analoge individuale printr-un convertor analog-digital si un discriminator. Cand un telescop este declansat pulsul semnal din fiecare din cele n[109 la Whipple Observatory] tuburi este integrat pentru Δt[=25 la Whipple] nanosecunde, digitalizat si inmagazinat ca fiind "unitati digitale"(du).O declansare a telescopului are loc atunci cand 2 dintre tuburile regiunii interioare verifica simultan un prag discriminator care corespunde la aproximativ 50 du.

Fiecare imagine inregistrata de catre telescop consta in atatea seturi de valori ale numa-rului de unitati digitale cati fotomultiplicatori contine telescopul(de exemplu la Whipple Observatory 109 valori).

Marimea pixelilor conduce la o anumita valoare a energiei de prag[4]. Pixel inseamna un pmt iar marimea sa se refera la apertura sa.

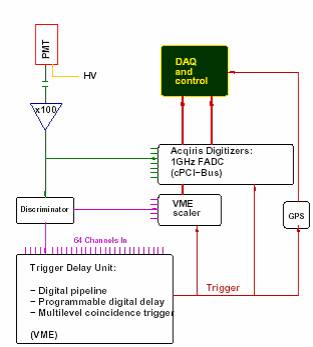
Fig.1.3 Desen reprezentand schema electronica utilizata in experimentul Stacee[10] unde simbolurile reprezinta: PMT-tub fotomultiplicator, HV-bloc de inalta tensiune,DAQ-blocul achizitiilor de date, Trigger Delay Unit-unitatea de intarziere a declansarii, FADC-numaratorul rapid analog digital, GPS-sistemul global de pozitionare

Intre experimentele enumerate anterior ca utilizeaza tehnica Cerenkov exista diferente in ceea ce priveste echipamentele utilizate. Diferentele constau in numarul telescoapelor utilizate, a marimilor oglinzilor, a numarului de tuburi fotomultiplicatoare, etc.

Tabelul I.Caracteristici ale unor telescoape sau matrici de telescoape (dupa [2]) .(valorile din paranteze sunt proiectate; intre timp unele date s-au schimbat[12])

1.2.Strategii pentru eliminarea fondului

Simularile Monte Carlo, impreuna cu detectiile realizate, arata ca fotonii Cerenkov proveniti din jerbele generate de catre cuantele gama primare reprezinta aproximativ 1% din fondul care insoteste fotonii.

In studiile timpurii ale cuantelor gama cosmice eliminarea fondului jerbelor generate ha-dronic din directii imtamplatoare s-a facut tinandu-se cont de a)marimea sau/si de forma imaginilor celor doua tipuri de jerbe, generate gama si generate hadronic; b)diferentele intre orientarea imaginii bazata pe directia spre origine, adica dupa directia sursei discrete sau a fondului izotropic.

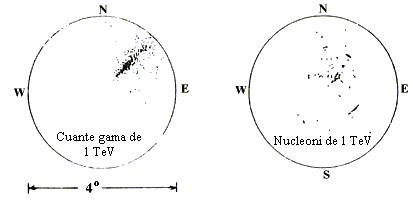
Fig.1.4 Reproduceri ale imaginilor detectate ale unei jerbe generate de catre cuante gama primare(stanga) si de catre hadroni(dreapta) dupa [1]

Exista mai multe strategii de eliminare a fondului care se bazeaza pe aceste caracteristici. Evaluarea eficacitatii fiecareia[7] dintre strategii se face cu ajutorul marimii:

Q=fractia de jerbe gama care indeplinesc criteriile de selectie/(fractia de jerbe a fondului care indeplinesc criteriile de selectie)^1/2 (1.2.1)

De exemplu in "analiza supertaieturilor" adoptata pentru a optimiza semnificatia statistica a semnalului inregistrat in 1988/89 dinspre constelatia Crabului valorile parametrilor geometrici au fost alese[7] :0,073<largime<0,15; 0,16<lungime<0,30; alfa<15,1;0,51<distanta <1,1

In prezent[7] se selecteaza acele imagini pentru care parametrii amintiti au valorile cu-prinse in anumite limite ce tin seama de configuratia camerei utilizate in experiment. Re-zultatul tipic pentru Q este 4.Folosirea acestor criterii de selectie are dezavantajul ca opereaza direct cu valori obtinute din extractia spectrului energetic al radiatiei, ori lungi-

mea si largimea jerbei cresc odata cu cresterea energiei.In aceasta situatie ar fi necesara adoptarea unor intervale ale marimilor celor 4 parametri diferite pentru fiecare domeniu de valori ale energiei. Pe de alta parte insa nici energia primara nu este bine cunoscuta. Marimea imaginii jerbei ofera o estimare a energiei primare, iar lungimea si largimea sunt corelate la randul lor prin logaritmul marimii jerbei.Valorile medii ale largimii, lungimii si unghiului alfa sunt obtinute cu precizie din termenii de ordinul intai ale dezvoltarii polinomiale ale variabilei ln(marimea jerbei).

O alta strategie este cea a "supertaieturilor extinse" conform careia se selecteaza acele imagini ale caror valori ale largimii, lungimii, distantei si unghiului alfa ce se gasesc intr-un interval simetric fata de valorile medii ale acestor parametri. Aplicata la Whipple Observatory strategia a selectat 95% dintre imaginile simulate. In aceasta strategie criteriile au fost:

largime+0,022-0,023 ln(marime) <0,048

lungime - 0,114 - 0,020(marime) <0,068

alfa - 9,16 +0,558 ln(marime) <13,5

Ambele strategii se bazeaza pe masurari directe ale marimii jerbei. Folosirea para-metrilor largime, lungime, distanta, unghiul alfa are avantajul ca acestia pot fi folositi atat individual cat si in combinatii in stabilirea unor criterii de selectie. Alte strategii se bazeaza pe simulari de jerbe atmosferice:"

O imbunatatire a coeficientului Q s-a obtinut in experimentul Whipple Obsevatory utilizand criteriile de selectie a imaginilor "fereastra elipsoidala a radiatiilor gama"[7].

Pentru a intelege aceasta metoda sa observam figura urmatoare:

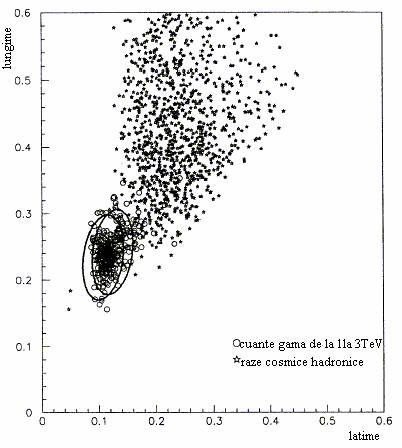
Fig.1.5 In aceasta figura sunt reprezentate lungimea si latimea evenimentelor produse de cuantele gama si care au fost obtinute prin simulare, urmele acestor jerbe fiind reprezentate prin cercuri. Evenimentele fondului sunt reprezentate prin stele iar dimensiunile sale sunt cele din datele experimentale. In figura au fost incluse doar imagini pentru care si distanta [7] .

Se poate constata ca se poate delimita o regiune elipsoidala in spatiul parametrilor unde se gasesc imagini ce pot fi acceptate. Pe figura au fost delimitate in planul latime-lungime doua elipse, fiecare corespunzand unei valori a distantei, care poate fi considerata ca este masurata pentru o axa normala pe pagina. Aceasta metoda de selectie a imaginilor are urmatoarele avantaje:

.intrucat foloseste un domeniu mai ingust de valori ale parametrilor este mai eficienta in alegerea jerbelor produse de cuantele gama decat criteriile ferestrei rectangulare de acceptare folosite la "supertaieturi"; acest fapt se datoreste corelarii variatiilor unor parametri

.utilizeaza un algoritm de calcul al analizei unei aglomerari relativ simplu pentru defi-nirea unui astfel de elipsoid din proprietatile statistice unui esantion mare de imagini simulate; acesta utilizeaza conceptul de distanta Mahalonobis a unui punct in spatiul parametric fata de centrul "aglomerarii gama"ale punctelor acestui spatiu.

Exista astfel o familie de elipsoizi ce difera intre ei prin "razele" lor in acest spatiu para-metric multidimensional.In acest mod, la aplicarea criteriilor se va utiliza un singur para-metru ce va fi utilizat la optimizarea unui set de date experimentale. Fereastra de selectie se defineste in modul urmator. Fiind data o imagine cu parametrii originali

si notand abaterile fiecaruia valoarea medie asteptata pentru imaginile gama este

(1.2.2)

Atunci distanta Mahalonobis a punctului imagine fata de centrul aglomerarii este data de

(1.2.3)

unde matricea ce defineste metrica spatiului parametric este inversa matricii

(covariante) moment de ordinul doi

(1.2.4)

In experimentul HEGRA s-au utilizat criterii bazate pe utilizarea parametrului "Straluci-rea suprafetei [14] etc.

Fig. VII.1.6 Reprezentare a imaginii dupa eliminarea fondului

1.3.Amplificarea telescopului, aria de colectare

Pentru estimarea energiei radiatiei primare se utilizeaza simulari ce sunt confruntate cu semnalele inregistrate de catre telescoape. Valorile marimilor(parametrilor) ce caracteri-zeaza semnalele inregistrate, cum ar fi de exemplu marimea jerbei, depind de amplifica-rea pe care o realizeaza telescopul. Amplificarea totala a telescopului se poate determina [10] ori prin masurare directa ori prin calibrare cu ajutorul jerbelor atmosferice.

Lumina Cerenkov detectata depinde in medie de urmatorii factori:

Absorbtia luminii Cerenkov de catre atmosfera

Reflectivitatea oglinzilor. Este cunoscut faptul ca reflectivitatea oglinzilor scade cu tim-pul in principal din cauza depunerii de praf ,adeziunii acestuia prin forte de tip Van der Waals[15]

Eficienta cuantica a fotomultiplicatorilor. In prima metoda se considera valoarea anunta-ta de catre fabricant. In a doua metoda se masoara pe un subset de fotomultiplicatori.

Amplificarea combinata a PMT-urilor/cabluri/amplificator/sistemul adc.

Ultimii trei factori dintre cei enumerati mai sus dau amplificarea totala a telescopului. Determinarea acestei amplificari este importanta pentru extragerea spectrului radiatiilor primare.In metoda intai (a supertaieturilor extinse) sunt disponibile masuratorile directe ale parametrilor telescopului cum ar fi cele pentru reflectivitatea oglinzilor, pierderilor prin cabluri, etc. Prin aceasta se obtine avantajul ca se folosesc masuratori relativ simple, dar are dezavantajul ca amplificarea depinde de un set masuratori dintre care una totusi nu se masoara direct si anume transmisia atmosferica.

In metoda a doua programele de simulari Monte Carlo sunt folosite pentru a calcula rata declansarilor initiate de radiatiile cosmice. Apoi ratele simulate sunt comparate cu datele experimentale inregistrate pentru a se estima amplificarea totala a telescopului. In

aceasta metoda se obtine avantajul ca este suficienta o singura declansare generata de catre fondul de radiatii,insa dezavantajul tine de modelarea cascadelor radiatiilor secundare

Fig. 1.7 Reprezentare a imaginii realizate dupa calibrarea telescopului Whipple Observatory din observarea Nebuloasei Crabului( cu 37 de pixeli ) intre anii 1983-1985

Aria efectiva de colectare la o anumita energie se calculeaza considerand ca jerba cade aleator pe o suprafata suficient de mare A₀ (de exemplu un cerc de raza 250m)si ca se inregistreaza numarul de imagini ce declanseaza telescopul si care indeplinesc criteriile de selectie.in aceasta situatie aria pentru energia E este: A(E)=A₀ (numarul de imagini ce indeplinesc criteriile la E/numarul de imagini simulate la E).

Aria de colectare pentru jerbele provocate gama se poate calcula

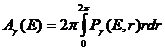(1.3.1)

unde reprezinta eficienta declansarii de catre jerbele gama de energie primara la o distanta a punctului de impact .Aria de colectare pentru jerbe de energie primara este determinata in principal prin aria efectiva a reflectorului telescopului

(1.3.2)

undeeste aria totala a oglinzii iar este eficienta conversiei foton-fotoelectron a canalelor camerei. Fiind data o arie fixa se poate obtine o arie de colectare maxima reducand pragul de declansare al telescoapelor. Dar la marginea energiilor joase acest prag este limitat de fluctuatiile fondului luminos din fiecare pixel al camerei.

1.4. Estimarea energiei; extractia spectrului

Problema estimarii energiei este importanta in cercetarea cuantelor gama cosmice de energie inalta intrucat concura la proiectarea unor modele de producere a cuantelor. Extragerea spectrului consta in stabilirea exponentului energiei si a limitei inferioare a energiei,pe de o parte,si in stabilirea probabiltatii cu care valorile acestor parametri sunt adevarate.

Estimarea energiei cuantelor gama primare se face pornind de la urmatoarele ipoteze:

. spectrul se considera a priori ca fiind de forma ,adica dependent de energia cuantelor dupa puterea

. raportul dintre puterea radio detectata si puterea gama detectata este la fel de mare cu raportul acelorasi puteri emise de sursa(Garmire si Kranshaar 1965);ipoteza aceasta

tine seama de faptul ca o sursa discreta ce emite radiatie sincrotronica contine si elec-troni de energie mare care emit gama.

Tehnica extragerii spectrului cuantelor gama primare a fost propusa si verificata pentru prima data in cadrul programului Whipple Observatory.Cu ajutorul ei au fost detectate cuantele gama de energii de ordinul TeV provenind de la pulsarul Crab. Tehnica a fost aplicata cu unele diferente in experimentele programelor HEGRA si CANGAROO. Algoritmul acestei tehnici comporta urmatoarele operatii[7]:

. se alege o metoda de eliminare a fondului, metoda trebuind sa fie predeterminata de eficienta impusa peste un ordin extins al energiilor cuantelor primare; se impun criterii de selectare a imaginilor jerbelor produse de cuantele gama primare, iar celelalte ce nu intrunesc conditiile impuse de catre criterii sunt eliminate

. se estimeaza aria de colectare a telescopului peste un domeniu extins de energii; aceasta arie depinde de maniera in care telescopul este "declansat" ca sa inregistreze o imagine si de eficienta metodei de selectie a imaginilor jerbelor electromagnetice

. se estimeaza energia cuantelor gama primare din caracteristicile imaginilor observate astfel incat sa se optimizeze rezolutia energetica a telescopului

. dupa ce energiile primare au fost estimate si daca ele sunt simetric distribuite fata de energia reala ce corespunde unui spectru rapid descrescator fluxurile corespunzatoare fiecarui interval energetic vor fi distorsionate de catre rezolutia energetica finita a teles-copului;acest lucru trebuie facut cu mare grija astfel incat sa se obtina dupa cum este asteptat un spectru energetic al sursei dependent de energie ca o lege de putere a energiei

. trebuie masurati direct sau estimati din datele experimentele parametrii telescopului (reflectivitatea oglinzii, amplificarea PMT. etc.);chiar si asa se introduce o incertitudine din cauza cunoasterii incomplete a transmisivitatii atmosferice a luminii Cerenkov

In experimentul din programul Whipple Observatory spectrul gama a fost extras prin doua metode, fiecare diferind de cealalta prin strategia de eliminarea a fondului si prin programul de simulare Monte Carlo. Utilizarea ambelor metode a permis verificarea vali-ditatii metodelor utilizate(cross-checking).Pentru prima metoda s-au folosit criteriile "su-pertaieturile extinse" pentru eliminarea fondului, iar aria de colectare si functia de rezolu-tie au fost calculate explicit.

In estimarea energiei se impune necesitatea utilizarii unor limite inferioara sii superioara a razei cercului de impact al jerbei cu solul. Aceasta intrucat in afara acestor limite apar distorsiuni[7] atat datorita dependentei densitatii laterale de raza de impact cat si datorita fluctuatiilor de la jerba la jerba.

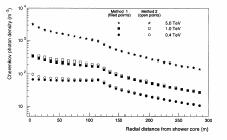
Fig. 1.8 Distributia laterala a luminii Cerenkov incidente simulata pentru mai multe energii. Se observa ca la o distanta de circa 130 m de inima jerbei apar distorsiuni ,iar pentru portiunea orizontala densitatea depinde de energie(dupa [7])

Aceste limite au fost alese in experimentul Whipple Observatory a fi 40 m si 125m[7]. De fapt nu raza de impact este cea care se masoara ci distanta unghiulara a centroidului imagine de la pozitia sursei in campul vizual .Ca urmare acestui parametru i se impun limite. In acelasi experiment aceste limite au fost 0,6⁰ si 1,0^0.

Cu metoda intai,dezvoltata in principal la Universitatea Iowa, energia fiecarei jerbe se estimeaza explicit. Notand cu si cu unde este energia reala a jerbei iar este energia estimata ,atunci[7]

x = - 8,11+2,56 ln (marime) - 9,25 distanta - 0,120 [ln(marime)]² +6,26 (distanta)² +

+0,0105 ln (marime)·(distanta)   (1.4.1)

Forma functiei de estimare de mai sus ,in care s-a folosit un polinom de gradul doi in ln(marime) si distanta pentru a descrie x , s-a potrivit cel mai bine cu simularile de jerbe

ce satisfac criteriile de selectie. Coeficientii polinomiali au fost astfel alesi incat sa minimizeze eroarea medie patratica, Σ( x - x )²,precum si eroarea absoluta Σ(x - x).

Pentru a compara raspunsurile diferitilor detectori la stimulii surselor si pentru estimarea unui flux absolut al radiatiilor gama peste un prag predeterminat al energiei este utila fo-losirea parametrului energie de prag. Pentru energii TeV nu exista inca un consens in definirea acestui parametru. Unii autori[7] au adoptat prescriptia lui Weekes(1976) de definire a "energiei de prag traditionale" ca fiind acea energie la care frecventa de declansare telescopului ar fi egala cu cea realizata de o sursa cu spectrul avand exponentul integral 1,6. In acest mod aria efectiva de colectare este definita in termenii unui detector ideal cu o arie de colectare care este constanta deasupra energiei de prag si zero sub ea.

Pentru exemplificarea aplicarii acestei metode in experimente prezentam date numerice impreuna cu comentariile aferente pentru cateva dintre sesiunile de observatii in programul Whipple Observatory

a)conditiile tehnice in care s-a desfasurat sesiunea de observatii 1986-1988

Camera din planul focal al telescopului a continut 37 de tuburi fotomultiplicatoare cu fo-tocatozi bialcalini. Tuburile erau aranjate intr-o grila de forma hexagonala. Tuburile alese au fost foarte sensibile la lumina UV, avand o eficienta cuantica mare. Timpul de sosire al fiecarui eveniment a fost masurat cu o precizie mai ridicata decat 0,5 ms si cu o pauza intre evenimente de 1μs.In conditiile de operare(noapte intunecoasa)curentul mediu din fiecare tub fotomultiplicator a fost de 0,33 fotoelectroni pe nanosecunda. Timpul de integrare al camerei a fost de 45ns.Declansarile realizate artificial ale camerei au condus la masurarea numarului de fotoelectroni per canal si per largime a portii;acesta a fost de 5,9.Numarul minim posibil de fotoelectroni per canal si per largime poarta a fost de 3,9; aceasta valoare constituie de fapt si deviatia Poisson standard. Observarile ON si OFF s-au facut pe durate de 28 de minute; sursa s-a gasit sub un unghi de ±0⁰,1 fata de axa optica a telescopului.

b)calibrarea consta in reducerea valorilor primare ale semnalelor inregistrate la valori ce tin seama de amplificarea telescopului.

In imaginile de mai jos se poate vedea cum arata imaginea initiala, adica inainte de calibrare si cum a aratat dupa calibrare (Fig. 1.8)

Fig. 1.9

S-au sustras din fiecare pixel asa-numitele valori piedestal, valori ce au ramas in general stabile in timpul detectiilor. Aceste valori s-au situat,dupa cum se poate constata, in jurul numarului de aproximativ 20 valori digitale.Ele reprezinta contributiile partilor electronice, de exemplu,la valorile semnalelor inregistrate. Marimea de 20 unitati digitale a fost prestabilita prin masurarea sau estimarea amplificarii telescopului. In plus,pentru a elimina efectele fluctuatiilor din noptile cu aglomerari de "zgomot", pentru masuratori, din anumite imagini ,s-a stabilit ca in tuburile fotomultiplicatoare in care semnalul a fost mai mic decat 10 unitati digitale( adica 14 fotoelectroni) sa se considere ca semnalul a fost nul. Acest prag de 14 fotoelectroni corespundea unei valori digitale de trei ori mai mare decat valoarea medie patratica si a fost stabilit prin simulari,simulari in care sa se obtina un prag de utilizare optima a camerei. S-au mai anulat semnalele din canalele in care valorile pulsurilor au fost mai mici decat 1% din suma incarcarilor tuturor canalelor. Aceasta din urma precautie a fost adoptata pentru a elimina semnalele mici aflate la distanta mare de centrul imaginii. Si aceasta valoare a fost obtinuta prin simulari.

c)selectarea imaginilor; eliminarea fondului

Pentru selectarea imaginilor se pot utiliza mai multe criterii de selectie. In experimentele Whipple Observatory,in sesiunile 1983-1985 si dec1986-feb1988,s-au utilizat doua stra-tegii de selectie: una in care s-au limitat valorile parametrului combinat azlat si alta in care selectia s-a facut prin utilizarea unor limite impuse celor 3 parametri independenti, latime, lungime si concentratie .

Limitele impuse in ambele strategii au fost determinate cu ajutorul simularilor Monte Carlo. Simularile au estimat raspunsurile camerelor telescoapelor la jerbele generate de catre cuantele gama primare si de catre protonii primari. De remarcat faptul ca in simulari s-au folosit parametrii reali ai camerelor. Simularile au fost realizate in conditiile in care camerele ar fi indreptate spre zenit(care ar fi si directia sursei),iar exponentii energiei pentru spectrele diferentiale ale celor doua tipuri de jerbe au fost presupusi a fi -2,2 pentru gama si -2,65 pentru fondul hadronic. In tabelul de mai jos sunt prezentate limitele (taieturile) impuse parametrilor imaginilor, pentru

Tabelul II

Se poate constata din tabel ca pentru ficare zona a camerei s-au impus alte valori ale li-mitelor; aceasta intrucat tuburile fotomultiplicatoarea din zone diferite au sensibilitate

spectrala diferita. Limitele au fost calculate in simulari astfel incat in fiecare dintre domeniile alese sa existe maximum de evenimente generate gama si contaminare minima cu fond al jerbelor hadronice.

S-au impus aceste limite datelor inregistrate in perioada dec1986-feb1988:

Tabelul III

Semnifictia statistica a observarilor din perioada dec1986-feb1988 este

(1.4.2)

Ca urmare a aplicarii limitelor impuse parametrului combinat azlat s-au stabilit urmatoa-rele valori:

Tabelul IV

Din acest ultim tabel se poate constata marirea semnificatiei statistice fata de situatia imaginii careia nu i s-a aplicat selectia.Pe de alta parte daca in prima situatie excesul de evenimente ON reprezenta 0,2% din numarul de evenimente OFF,in a doua situatie excesul reprezinta 14,7% din numarul de evenimente OFF.Se mai poate constata ca ex-cesul nu s-a modificat in valoare absoluta semnificativ.

Utilizand definitiile (II.4.5)-(II.4.10) si masurand coordonatele pixelilor incarcati se calculeaza valorile parametrilor latime,lungime,distanta,deplasarea imaginii si parametrul combinat azlat.Exemplificare:fie tabelul urmator cuprinzand coordonatele si incarcarile pixelilor din fig.1.9

Tabelul V

(Nota:valorile si unitatile de masura ale coordonatelor sunt fictive si au fost propuse pentru exemplificarea prelucrarii imaginilor )

Din valorile acestui tabel rezulta

(1.4.3)

(1.4.4)

(1.4.5)

(1.4.6)

(1.4.7)

(1.4.8)

(1.4.9)

(1.4.10)

(1.4.11)

(1.4.12)

(1.4.13)

(1.4.14)

(1.4.15)

distanta= (1.4.16)

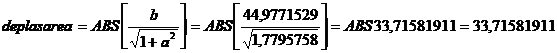
(1.4.17)

Rezultatele de mai sus pot fi ale unei observari ON sau ale unei observari OFF.Ansam-blul unei observari ON si al unei observari OFF din timpul aceleasi sesiuni de observari se numeste pereche ON/OFF.

Valorile reale ale parametrilor imaginii sunt prezentate in tabelul de mai jos:

Tabelul VI

d)stabilirea fluxurilor detectate se face cu ajutorul exceselor detectate, al timpilor de ob-servare si al ariilor de colectare

Ariile de colectare depind de energiile cuantelor gama primare si de unghiul de zenit si se stabilesc prin simulari Monte Carlo.

Astfel intr-o sesiune de observari, aplicandu-se limitele parametrului azlat pentru z<30⁰, s-au adunat 574 de evenimente din zona 1 si 463 din zona 2,pentru timpul de observare de 116·28 minute in ariile de colectare de π(88m)² in zona1 si π(117m)² in zona2.Atunci fluxul este

(1.4.18)

pentru cuante gama mai mari de 0,7 TeV.

Daca insa se tine cont de rezolutia energetica a telescopului si de spectrul sursei atunci in calculul fluxului se utilizeaza aria de colectare modificata. In plus fluxul poate fi calculat si in raport cu unitatea de energie a intervalului energetic pentru care se face calculul. In tabelul urmator sunt prezentate valorile unor astfel de fluxuri pentru o sesiune de observari in perioada 1988-1989

Tabelul VII

Pentru intervalul energetic ΔE=0,217 TeV

(1.4.19)

e)stabilirea spectrului consta in fapt in aproximarea distributiei aleatoare a cuantelor ga-ma cu o lege in care numarul de cuante emise depinde de energiile acestora dupa o lege de putere a energiei .In prima metoda "potrivirea" datelor experimentale cu aceasta lege s-a facut prin varierea energiei limita si a exponentului in asa fel incat abaterea medie patratica ale valorilor experimentale ale fluxului detectat fata de cel as-teptat sa fie minima

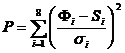(1.4.20)

unde este valoarea fluxului detectata in determinarea i, valoarea calculata a fluxului corespunzatoare aceleiasi determinari, iar deviatia standard. Exista mai

multe tehnici de minimizare a expresiei de mai sus;ele se raporteaza la tipul dependentei functieide variabilele de care depinde, precum si de tipul de distributie pe care o au diferentele.Tehnica minimizarii se gaseste in literatura de specialitate si sub numele de "metoda micilor patrate". Tipurile de distributii sub care se imprastie diferentele sunt Poisson, Gauss(normala) sau "hi patrat" .In conditiile in care numarul de determinari ale unei distributii Poisson este mare distributia se aseamana cu cea Gauss. La randul ei functia poate fi liniara sau nu in raport cu parametrii care trebuie ajustati. In situatia in care dependenta este liniara problema se poate rezolva analitic. In alte situatii, cum ar fi cea a unor dependente exponentiale expresia se poate liniariza prin logaritmare. Pentru situatii in care dependentele nu sunt in general liniare au fost propuse numeroase tehnici de minimizare. Una dintre ele, numita "cautare retea" ,se realizeaza numeric astfel: se imparte domeniul de definitie al parametrului ajustabil in intervale si se calculeaza valoarea functiei pe fiecare interval, pana se gaseste valoarea minima. Alte metode se numesc de tip gradient, de tip simplex etc.[16].In prezent au fost puse la punct mai multe programe soft de calcul al minimului [17],[18].Daca fluxul se considera a avea forma atunci aceasta expresie se poate liniariza prin logaritmare: si prin metoda micilor patrate se poate gasi valoarea minima pentru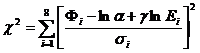intocmai dupa cum se procedeaza la liniarizarea oricarui set de determinari experimentale ale caror dependenta se asteapta sa fie liniara. Fata de abordarile in care nu este cazul sa se tina seama de "incarcarile" semnalelor ,in exemplul setului de date prelucrat in acest paragraf este necesar ca datele sa fie normate.

Notand 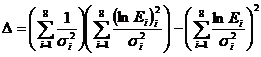(1.4.21)

atunci

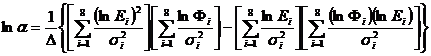(1.4.22)

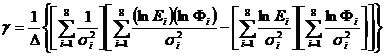   (1.4.23)

unde din tabelul de mai sus, fluxurile din ultima coloana a tabelului, iar abaterile standard ce insotesc in tabel valorile fluxurilor.

Cu valorile din tabel se gasesc:

(1.4.24)

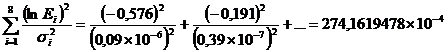   (1.4.25)

   (1.4.26)

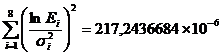(1.4.27)

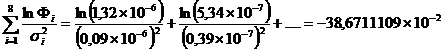(1.4.28)

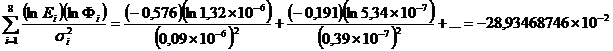(1.4.29)

Introducand aceste valori in relatia(1.4.22)   se obtin si (gama este negativ intrucat in calcule s-a considerat valoarea sa algebrica) de unde .Cu aceste valori ale celor doi parametri ajustabili se poate calcula valoarea functiei .Calcule mai exacte, ce tin cont si de aria de colectare modificata, au condus la valorile , ,respectiv.In alte experimente in care s-au masurat fluxurile dinspre Nebuloasa Crabului spectrul a deviat de la forma de lege putere[7] Tehnica minimizarii expresiei de mai sus tine cont de faptul ca are o distributie normala. Aceasta tehnica poate fi aplicata oricarei observabile ale carei date experimentale prezinta o imprastiere ce poate fi descrisa de o lege liniara sau nu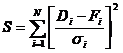undereprezinta valoarea asteptata a marimii fizice care cores-punde datelor experimentale,iarabaterea standard asteptata a marimii fizice[19] . Daca in aceasta expresie s-ar inlocui sicu valoarea medie pe fiecare interval i, cu valoarea asteptata, respectiv cu abaterea standard, atunci fiecare termen al sumei ar fi patratul unei variabile,ale unei unitati de variatie independenta, de medie nula. Conform teoremei limitei centrale, daca in acelasi interval al marimii fizice se inregistreaza un numar mare de evenimente, atunci acestea sunt distribuite normal. Cu valorile adevarate ale lui si ale lui , devine

(1.4.30)

adica o forma patratica careia ii corespunde o matrice identitate .Rangul ei este .Modelul distributiei acestei forme patratice este distributia de tip cu grade de libertate(Cramer,p234).Se defineste

(1.4.31)

unde se numeste abaterea datei experimentale de la cea mai buna ajustare fata de modelul prezis. Prin cea mai buna ajustare se intelege situatia in care parametrii mo-delului au fost ajustati ca sa minimizeze .De remarcat este faptul ca dependentele

parametrilor modelului prezis nu trebuie in mod necesar sa fie liniare, dar sa fie de doua ori diferentiabile. S-ar putea crede ca abaterile sunt independente unele de altele, dar nu este asa. Cea mai buna ajustare introduce o dependenta intre ele. Cramer arata ca exista o transfomare neortogonalaastfel incat unde este vectorul abatere adevarata de componente prezentate mai sus.Rangul formei patratice se arata ca este mai mic decat al formei cu un numar ,unde numarul este numarul para-metrilor ajustabili neechivalenti. Acest rezultat conduce si la afirmatia ca este distri-buit cu grade de libertate. In experimentul Whipple; cei doi parametri au fost si .Intrucat rezulta ca cea mai buna ajustare se face pentru 6 grade de li-bertate.

Cu datele din tabelul de mai sus s-a obtinut pentru 6 grade de libertate lasi (aici este modulul ).Cu aceste valori spectrul ridicat pentru sesiunea de determinari din 1988-1989 se scrie

(1.4.32)

Evaluandu-se intervalul de incredere pentru care este adevarat acest spectru se poate ridica un contur in plan al punctelor pentru care ia valoarea minima, cel interior in desenul de mai jos

Fig.VII.1.10

Urmatoarele contururi sunt desenate pentru valori ale lui care cresc cu o unitate. Conturul desenat cu linie intrerupta corespunde lui pentru care nivelul de incredere este de 68% pentru si .

Pentru verificarea metodelor utilizate in extragerea spectrelor adeseori se folosesc si alte metode. Se face astfel o verificare incrucisata. In experimentul Whipple din 1988-1989 s-a mai folosit o metoda pentru extragerea spectrului. In aceasta metoda s-au folosit alte criterii de selectie(fereastra elipsoidala),iar extractia s-a facut prin ajustarea datelor de intrare a programului Monte Carlo de simulare a jerbelor atmosferice pana cand se potrivesc cu imaginile selectate ale celor inregistrate. In aceasta a doua metoda nu mai este necesara estimarea ariei de colectare si nici estimarea rezolutiei energetice.

Rezultatele celor doua metode au fost in acord.

1.5. Dezvoltari ale tehnicii imagistice cu lumina Cerenkov

Dintre toate tehnicile de detectie a cuantelor gama cosmice de energie foarte inalta cea mai eficienta este cea bazata pe lumina Cerenkov.Acest fapt este confirmat de detectiile pe care detectorii acestia le-au facut: descoperirea surselor extragalactice de radiatie gama de energie foarte mare. Deasemeni investitiile in detectia cuantelor gama se fac in detectori de acest tip.

Experimentul HEGRA foloseste in prezent un sistem stereoscopic pentru detectia cuantelor gama, adica mai multi "ochi" ce vad lumina Cerenkov. Utilizarea sistemului stereoscopic permite o mai buna determinare a directiei de sosire a radiatiei primare si deci o mai buna estimare a energiei primare.

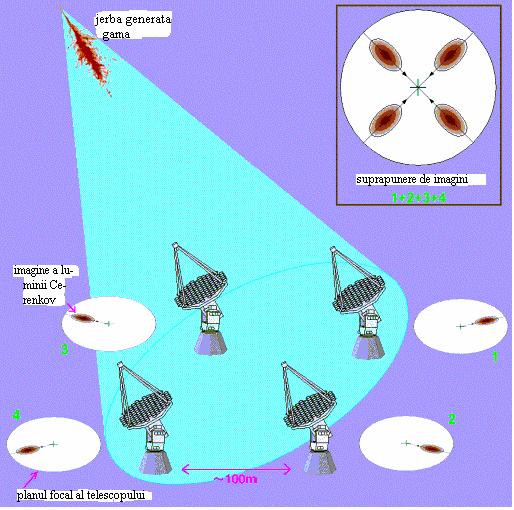
Fig. VII.1.11 Desen reprezentand un sistem stereoscopic cu patru "ochi"

Tot in experimentul HEGRA s-au imbunatatit criteriile de eliminare a fondului, adoptan-duse "limitele dinamice" pentru parametrii Hillas [20].In acest sistem de criterii se mareste timpul de observare "off" fata de cel "on" prin utilizarea masuratorilor facute cand sursa gama nu este observata. Cu acest sistem de criterii a crescut eficienta detectiilor gama de energii mari pentru unghiuri de zenit mici si a jerbelor cu parametrul de impact mic.

Limita de 200 GeV impusa observarii jerbelor produse de cuantele gama prin detectia luminii Cerenkov de catre fondul cerului de noapte si fara luna a condus la imbunatatirea detectiei si pentru noptile cu luna, deci la coborarea pragului amintit.

Viitorul experiment VERITAS va realiza o sensibilitate foarte mare pentru energii coborate si apertura mare a detectiei prin operarea telescoapelor in paralel(modul sensibil).[21]

2.Retele la sol de detectori de particule secundare incarcate

In regiunea energiilor peste 40 GeV destul de multe particule secundare incarcate ajung la sol prin intermediul jerbelor atmosferice extinse(EAS).Acestea pot fi detectate cu ajutorul retelelor de detectoare cu scintilatori. Avand campul de vedere(field of view FOV) complet extins la intreaga bolta cereasca ele pot observa 24 de ore din 24 toate sursele simultan. Calitatea observatiilor lor nu este influentata de conditiile meteorologi-ce .Detectorii acestor retele nu acopera insa toata suprafata solului unde reteaua este plasata. Acest fapt face ca reteaua sa nu detecteze decat o parte a particulelor secundare incarcate ce ating solul. Pentru a realiza detectia cuantele gama primare trebuie sa aiba energii suficient de mari pentru a genera cascade cu numar mare de particule secundare. Se spune ca retelele de acest tip au energii de prag mari, mai mari decat ale telescoapelor sau retelelor de telescoape Cerenkov. In experimentul Tibet s-a reusit totusi obtinerea unor energii de prag coborate.[3]

Detectorii cu scintilatii utilizati la sol se aranjeaza in retele astfel incat sa acopere aria ce urmeaza a fi monitorizata sub forma unei grile in care distantele intre detectori variaza de la experiment la experiment(EAS ground array). In experimentul Pierre Auger [22] distanta va fi de 1-1,5km.

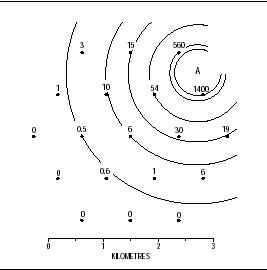
Fig.2.1 Figura reprezinta dispunerea in teren a detectorilor cu scintilatii utilizati in experimentul Volcano Ranch; punctele reprezinta pozitiile detectorilor iar cifrele de langa ele densitatile(pe m²) de evenimente ale unei jerbe cu energii de peste 10²⁰eV(reproducere dupa [22])

Aceste retele de detectori la sol constituie mari calorimetre de esantionare, asemanatoare celor folosite in experimentele din laboratoare[22], dar avand un strat detector localizat la adancimea maxima X_max si care este mult mai putin dens. Atmosfera joaca rolul materialului absorbant al calorimetrului, adica placile de plumb sau otel.

Pentru detectorii cu scintilatie materialele utilizate sunt cristalele scintilatoare care au proprietatea ca atunci cand sunt ciocnite de particule de energii mari emit lumina.

Fig.2.2 Desen reprezentand procesul de scintilatie

Radiatiile gama primare genereaza in cristale particule incarcate ce emit lumina. La trecerea prin cristalele scintilatoare fotonii produc imprastieri Compton, perechi e⁺e^- si fotoabsorbtie. Insumand energiile eliberate in astfel de procese se poate afla energia radiatiilor primare. Cele mai obisnuite scintilatoare[1] se fac din iodura de sodiu NaI sau iodura de cesiu CsI. Pentru a ajuta aceste materiale se introduc mici cantitati de impuritati numite "activatori" cum ar fi de exemplu thallium sau sodiu. In aceasta situatie materialele detectorilor se simbolizeaza NaI(Tl) sau CsI(Na). Retelele tipice de detectori

scintilatori desfasoara[1] intre 100m² si 1000m² de material scintilator dispersat pe o

suprafata de 10⁴ m² sau chiar pana la 10⁵ m² de teren. Avand o asa de mare suprafata de esantionare a particulelor ele sunt sensibile doar la cuantele gama cosmice de energii ~100 TeV.Recente progrese datorate de exemplu ridicarii detectorilor la altitudini mai mari au condus[2] la o energie de prag sub sau aproape de 1 TeV. Acesti detectori "vad" intreaga bolta cereasca si lucreaza continuu. Un exemplu de astfel de detector este cel din colaborarea Tibet construit la altitudine mare(4 km asl) [2].La aceasta altitudine mult mai multe jerbe supravietuiesc pana la sol.

Fig. 2.3 Fotografie a retelei de scintilatori a programului Tibet(reproducere dupa [23])

Fig. 2.4 Desen reprezentand dispunerea detectorilor in experimentul Tibet(reproducere dupa [23])

Alte experimente experimente de detectia cuantelor gama cosmice de energie inalta de tip " EAS ground array" sunt :AGASA,SPASE,GRAND,GREX

Retelele de detectori de la sol sunt proiectate si utilizate pentru masurarea densitatii laterale a particulelor[2],[22] din jerba la sol si a timpilor de sosire a acestor particule la sol pentru diferite distante fata de ceea ce se numeste "miezul" jerbei. Cu ajutorul densitatii laterale(sau profilul lateral) se poate determina energia radiatiilor primare prin intermediul simularilor[22].In experimentul grupului Volcano Ranch estimarea energiei primare s-a facut pe baza unor considerente ce au tinut cont de calcule de dezvoltare a cascadelor jerbelor atmosferice si nu pe baza utilizarii unor simulari de tip Monte Carlo.Timpii relativi de sosire sunt folositi la reconstructia directiei radiatiei primare cu o

precizie de 2⁰ sau chiar mai buna[22].Intrucat densitatea laterala este sensibila atat la compozitia primara cat si la modelul de interactiuni utilizat se alege[2] ca densitate de referinta in determinarea energiei primare, densitatea particulelor la distanta de 600m,intrucat asa dupa cum rezulta din simulari aceasta nu mai este sensibila la cei doi factori. Particulele pot fi atat primare cat si secundare. Cu ajutorul timpilor de sosire masurati se poate reconstrui directia radiatiilor primare[12].

Asa dupa cum am aratat mai inainte particulele secundare din jerbele atmosferice, pe masura ce jerba evolueaza in atmosfera,se imprastie fata axa jerbei, adica directia de sosire a radiatiei primare. Planul tangent la frontul jerbei pe axa jerbei se numeste planul jerbei. Frontul jerbei este curbat intrucat nu toate particulele din jerba se propaga cu aceeasi viteza. Punctul continut in planul jerbei si al axei jerbei totodata se numeste miezul jerbei.Miezul jerbei este asemanator unei surse de particule ce se deplaseaza de-a lungul axei jerbei. Departe de miezul jerbei particulele sunt intarziate cu o dipersie

temporala in general proportionala cu distanta pana la miezul jerbei[22].Aceasta impras-tiere temporala creste odata cu cresterea adancimii maxime. Muonii tind sa ajunga mai

devreme decat electronii si fotonii intrucat ei sufera mai putine imprastieri si astfel au o cale mai directa spre sol.

2.1.Determinarea directiei de sosire a cuantelor gama primare

Ordinea logica de determinare a directiei radiatiei primare se prezinta dupa cum urmeaza. Initial se determina ceea ce se numeste centrul de gravitatie al jerbei, adica punctul in care jerba ce atinge solul contine si axa jerbei. Apoi pentru determinarea axei jerbei si deci a directiei radiatiei primare se tine cont de simetria circulara a jerbei fata de axa. Jerbele care sosesc vertical sau aproape de verticala locului vor lovi solul dupa un contur circular.Daca jerba are o pozitie oblica, adica mai departe de zenit atunci inter-sectia dintre planul solului si cascada este de forma eliptica .Ca urmare directia se

construieste ca fiind directia perpendiculara pe planul jerbei in punctul in care inima jerbei a atins solul si care se numeste centrul de gravitatie(cog in engl centre of gravita-tion).

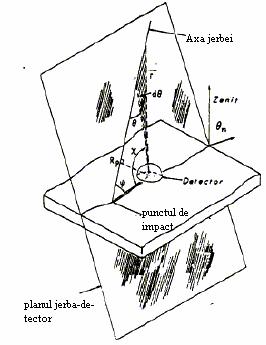
Fig. 2.5 Desen reprezentand geometria detectiei unei jerbe

Daca trei statii[22] inregistreaza jerba atunci directia jerbei se calculeaza prin metoda triangulatiei. Daca sunt mai mult de trei detectori atunci se utlizeaza o metoda patratica. Cu ajutorul directiei axei solului se calculeaza distanta laterala a detectorului.

2.2.Estimarea energiei cuantelor gama primare

Pentru estimarea energiei radiatiilor primare se interpoleaza si/sau extrapoleaza masuratorile densitatii laterale a numarului de particule(sau mai degraba a energiei absorbite de la particula incarcata de catre detector pe unitatea de suprafata) la suprafata solului la o cantitate a aceleasi densitati dar obtinuta prin simulare astfel incat acestea sa se potriveasca pentru o anumita energie primara presupusa in simulare[22].

2.3.Eficienta detectiei cuantelor gama de energie inalta cu detectori cu scintilatie

Exista opinia ca detectia cuantelor gama de energie foarte inalta cu detectori cu scintila-tie nu este eficienta[12],[8].Motivul ar fi acela ca pentru energii mai mari decat 30 TeV aceste sisteme au o slaba capacitate de a discerne intre jerbele produse de catre cuantele gama si cele produse de catre razele cosmice[12].Totusi autorii acestor opinii recunosc urmatoarele calitati ale acestor detectori: arii mari de colectare(>10000m²), foarte buna rezolutie unghiulara(~0,5⁰), rezolutie moderata a energiei(~100%), apertura FOV mare (~2sr) si ciclu de utilizare permanent(~100%).Tocmai acest din urma para-metru a facut ca spectrul diferential al sursei Mrk 501 sa fie imbunatatit in experimentul Tibet fata de experimentul Whipple Observatory,unde ciclul de utilizare a fost de 10% [25].Tot datorita ciclului de utilizare permanent in experimentul HEGRA s-a folosit o re-tea de scintilatori pentru observarea fondului difuz gama in domeniul 1-100 TeV[9]. Pentru a imbunatati capacitatea scintilatorilor in discernerea jerbelor generate gama de cele generate hadronic s-a observat ,din simularile Monte Carlo, ca acestea din urma se dezvolta mai incet dupa adancimea maxima astfel incat ratia log₁₀(N_s/L₉₀) la o pozitie fixa este presupusa mai mare pentru jerbele hadronice decat pentru cele gama [9].Marimile N_s si L₉₀ reprezinta numarul de fotoni si electroni ajunsi la detector, respectiv densitatea laterala a cascadei de fotoni Cerenkov masurate in detectie cu lumina Cerenkov. Prin urmare o imbunatatire a detectiei cu scintilatori,realizata in experimentul HEGRA este utilizarea simultana a acestei detectii impreuna cu cea cu lumina Cerenkov [9]. Simularile Monte Carlo au aratat ca parametrii formei distributiei laterale, determinati ca sa se potriveasca cu datele experimentale colectate de scintilatori, au un potential mai mare de discernere intre jerbele produse hadronic de cele produse gama decat parametrul 1/R_L. R_L= -1(d lnρ(r)/dr) este raza luminii Cerenkov la o distanta 50m<r<120m de inima jerbei[9].

Ideal ar fi ca telescoapele sa aiba un timp de lucru cat mai lung si o apertura mare precum a retelelor la sol pentru regiuni energetice cum sunt cele explorate de telescoapele Cerenkov. Astfel s-ar explora intreg cerul la energii de ordinul TeV. Pentru a realiza aceste deziderate cu o retea EAS, aceasta ar trebui ridicata la altitudini si mai mari, pen-tru a detecta o fractie mai mare de particule incarcate ce ajung la sol, sau de a mari sen-

sibilitatea la detectia fotonilor ce ajung la sol de catre EAS .Experimentul Milagro incor-poreaza aceste ultime doua idei ajungand la un prag de 250 GeV in conditiile mentinerii unui timp de lucru(duty factor) mare si a unei aperturi mari[3].

3.Detectori de lumina de fluorescenta

Sunt utilizati pentru determinarea profilului longitudinal, adica a dependentei numarului de particule secundare de adancimea in atmosfera si apoi de aici, pentru determinarea energiei primare.In deplasarea lor prin atmosfera radiatiile secundare alcatuite din particule incarcate excita moleculele de azot ,iar acestea prin dezexcitare emit radiatii in domeniul apropiatUV,300nm-400nm[22].Lumina emisa este practic izotropa[24].De la o anumita distanta detectorul in fluorescenta vede jerba ca un spot de lumina a carei miscare este de-a lungul axei jerbei. Intensitatea luminii de fluorescenta, corectata din punct de vedere al efectelor geometrice si atmosferice, reflecta dezvoltarea longitudinala a jerbei, N=N(X), si integrala sa este proportionala cu energia cedata atmosferei. Am notat cu X adancimea la care se afla jerba la un moment dat,adancime care se masoara in g cm^-2 . Tehnica detectiei cu ajutorul fluorescentei are marele avantaj ca masoara direct cascadele electromagnetice la nivelul solului oferind astfel o masurare calorimetrica a energiei jerbei pentru fiecare impact in parte si aceasta independent de modelele utilizate pentru simularea jerbelor,independent de compozitia primara si de variatiile in adancimea maxima a cascadei. Rezolutia energetica tipica in aceasta tehnica este de 20% pe cand in celelalte tehnici ajunge la 40%[5] .Se determina direct si adancimea maxima.

Detectia prin fluorescenta poate fi utilizata[24] atat pentru jerbele produse de catre radiatii primare incarcate cat si de catre cele neutre cum sunt radiatiile gama. Aceasta tehnica a fost folosita de exemplu intr-unul dintre experimentele Fly's Eye[2].

Experimentul Pierre Auger Observatory este proiectat sa utilizeze un sistem hibrid de detectie: detectori de particule incarcate(EAS array) si detectori de fluorescenta, pentru observari in domeniul energetic mai mare decat 10¹⁹ eV. Pana in prezent nici un experi-ment nu a evidentiat posibilitatea existentei unor cuante gama primare de energii atat de mari,dar exista lucrari ai caror autori admit posibilitatea existentei unor astfel de cuante

sau pun in discutie acest lucru. In aceasta situatie am considerat ca este justificat sa informam cititorul despre tehnica luminii fluorescente.

3.1 Determinarea directiei axei jerbei si a timpilor de sosire

Reconstructia directiei de deplasare a jerbei se face cu ajutorul planului detector-jerba (SDP). Axa jerbei este constransa sa se afle in acest plan ce contine detectorul cu fluorescenta si directia de observatie a unui anumit pixel spre jerba. Acest plan se determina prin compararea semnalelor colectate in fiecare tub dupa mai multe directii si alegerea directiei pentru care semnalul atinge amplitudinea. Vectorul normal la acest plan poate fi determinat[22] cu o precizie de 0,2⁰. Intr-o a doua etapa se determina orientarea si pozitia axei jerbei inauntrul SDP.

3.2 Determinarea energiei primare

Energia primara se estimeaza din cantitatea de totala de fluorescenta[2] conform relatiei[22]:

E_em= (E_c/l_r N_e(x)dx (3.2.1)

unde E_em este energia totala disipata pe cale electromagnetica, E_c/l_r este raportul dintre energia critica a electronilor si lungimea de unda a radiatiei,iar N_e(x) este numarul de electroni observat in jerba ca o functie de adancimea atmosferica x.

Intrucat o particula incarcata din cascada depoziteaza[22] in medie 2,2 MeV in atmosfera in fiecare interval de adancime de 1g/cm² atunci relatia de mai sus se poate scrie

E_em= 2,2 MeV/g/cm² N_e(x)dx    (3.2.2)

Intr-o abordare riguroasa N_e ar fi trebuit sa fie numarul total de particule incarcate din jerba. Intrucat insa numarul de electroni este mult mai mare decat al celorlalte particule s-a folosit in calcul numarul de electroni[22].Totusi dupa efectuarea calculelor cu acest numar se face o corectie de circa~10% la valoarea energiei totale primare E_em pentru a tine seama de existenta si celorlalte particule incarcate (muoni,neutrini, hadroni,etc.) din jerba. Deducerea lui N_e din cantitatea de fluorescenta detectata depinde de cunoasterea cu precizie a factorilor responsabili de producere a luminii si de transmisia prin aer, de calibrarea sistemului optic de detectie si de determinarea traiectoriei[22].Marimea

energiei electromagnetice ce atinge solul se obtine printr-o aproximare a unei forme

functionale la profilul longitudinal si integrarea sa pe o suprafata de detectie. Dar aceasta energie este o limita inferioara a energiei radiatiei primare, intrucat din ea lipseste o cantiate ce corespunde energiei transportate de muoni si neutrini. Energia neluata in calcul poate fi estimata din densitatile de muoni masurate de catre retelele de telescoape la sol.

Informatii despre compozitia primara se pot afla din marimea numita "adancime maxima" si notata X_max (masurata g/cm²) la care jerba atinge maximul de densitate de particule. Media acestei adancimi este legata de energia primara E prin

<X_max>=X^'₀ ln(E/E₀) (3.2.3)

Aici X^'₀ este numit rata elongatiei iar E₀ este energia caracteristica ce depinde de com-pozitia primara[24].Daca se determina X_max si X^'₀ din profilul longitudinal al jerbei

masurat de catre detectorul de fluorescenta,atunci se poate determina E₀ ,deci compozitia primara,dupa ce se determina cantitatea de fluorescenta totala.

Bibliografie:

1. http:// www.imagine.gsfc.nasa.gov./docs/ask astro/ask an astronomer.html

2. Gus Sinnis.Current Status of VHE Astronomy,arXiv:astro-ph/9906242 v1 14 Jun 1999

3. J.F.McCullough-Status of the Milagro Gamma Ray Observatory ,HE 6.1.02, The 26th ICRC proceedings,vol.2 pag.369

4.Vacanti G.G.,et al.,Gamma-ray Observations of the Crab Nebula at TeV Energies,ApJ,377,467-479,1991 August 20

5.Bird D.J.,et al.,The High Resolution Fly's Eye ( HiRes ) Project

6.Tanimori T. Construction of New 7m Imaging Air Cerenkov Telescope of CANGAROO ,The 26th ICRC proceedings,vol.I pag.203

7. .G.Mohanty,S.Biller,D.A.Carter-Lewis,D.J.Fegan,A.M.Hillas,R.C.Lamb,T.C. Weekes,M.West,J.Zweerink,Measurement of TeV gamma-ray spectra with the Cherenkov imaging technique,Astroparticle Physics 9(1998) 15-43

8.J. Szabelski ,Cosmic Rays:Studying the Origin,The Andrzej Soltan Institute for Nuclear Studies Cosmic Ray Laboratory,2 July 1997,arXiv:astro-ph/9710191 v1 17 Oct 1997

9.Aharonian . F.A. et al., Limits on the TeV .ux of di.use gamma rays as measuredwith the HEGRA air shower array HEGRA Collaboration Astroparticle Physics 17 (2002) 459-475

10.Covault C. E et al., The Status of the STACEE Observatory, Proceedings of ICRC 2001: 2810 Copernicus Gesellschaft 2001

11.Weekes T.C.,et.,Observation of the TeV Gamma Rays from the Crab Nebula Using the Atmospheric cerenkov Imaging Technique,The ApJ,342:379-395,1989 July 1

12. Catanese M.& Weekes T.C.-VERY HIGH ENERGY GAMMA-RAY ASTRONOMY ;Invited Review to appear in Publ.Astron.Soc.of the Pacific,astro-ph/9906501,30 Jun 1999

13.Badran H.M.si Weekes T.C.,improvement of gamma-hadron discrimination at TeV energies using a new parameter,image surface Brightness,Astroparticle Physics 7(1997) 307-314

14.Petry D.si Kranich D.,Development of "Dynamical Supercuts" for the HEGRA 5 m² Cherenkov Telescope

15.Barrio J.A.,et al.,The Magic Telescope,Design study for the construction of a 17m Cerenkov telescope for Gamma-Astronomy above 10 GeV,March 1998,Version 5, University of Leeds

16. Leo W.R., Statistics and the Treatement of Experimental Data,Springer Verlag 1992 17. Numerical Algorithms Group: NAG Fortran Library, Mayfield House, 256 Banbury Road, Oxford, OX2 7DE, United Kingdom; 1101 31st Street, Suite 100, Downers Grove, Ill. 60515, USA

18. James F.E.,. Roos M: ``Minuit'', program for function minimization, No. D506, CERN Program Library (CERN, Geneva, Switzerland)

19.Lampton M.,et al.,Parameter Estimation in X-Ray Astronomz, ApJ,208, 177-190, 1976 August 15

20.Petry D.si Kranich D.,Development of "Dynamical Supercuts" for the HEGRA 5 m² Cherenkov telescope

21.Weekes T.C. et al.,arXiv:astro-ph/0108478 v1 29 Aug 2001

23. Amenomori M., Performance of the Tibet-III Air-Shower ArrayThe Tibet AS Collaboration ,Proceedings of ICRC 2001: 573 Copernicus Gesellschaft 2001 ICRC 2001

24. Bhattacharjee .P si Sigl G.,Origin and Propagation of Extremely High Energy Cosmic Rays,arXiv:astro-ph/9811011 v2 Aug 1999

25.AMENOMORI M.,et al., (The Tibet ASc Collaboration) ApJ, 532:302»307, 2000 March 20