Proprietatile dielectricilor liniari, izotropi si omogeni

Proprietatile dielectricilor liniari, izotropi si omogeni

a. Susceptivitatea si permitivitatea electrica.

b. Dielectrici anizotropi.

c. Discontinuitatea vectorilor si la suprafata de separatie a doi dielectrici polarizati.

d. Energia campului electrostatic in dielectrici.

e. Condensatorii in prezenta dielectricilor.

f. Relatia Clausius - Mossotti.

g. Aplicatii.

a. Susceptivitatea si permitivitatea electrica

Asa cum am aratat in paragraful I.6.c., vectorul polarizare si vectorul intensitate a campului electric au aceeasi orientare. Deci intotdeauna in interiorul unui dielectric, in prezenta unui camp electric extern, apar dipoli electrici orientati in sensul campului aplicat.

Se numesc dielectrici perfecti sau liniari, dielectricii pentru care polarizarea, in orice punct, este proportionala cu campul electric aplicat. Pentru astfel de dielectrici, putem scrie:

                   (I.105)

unde se numeste susceptivitate electrica a mediului. Avand in vedere ceea ce am spus mai sus, intotdeauna este pozitiv.

Relatia fundamentala a mediilor dielectrice (vezi formula I.98) se transcrie astfel:

       (I.106)

Coeficientul

               (I.107)

se numeste permitivitatea absoluta a mediului.

Deoarece susceptivitatea electrica este intotdeauna pozitiva, rezulta ca permitivitatea absoluta a mediului este intotdeauna mai mare decat permitivitatea vidului.

Daca susceptivitatea electrica nu depinde de directia campului electric aplicat, mediul se numeste izotrop. In cazul in care susceptivitatea electrica este aceeasi in toate punctele dielectricului mediu se numeste omogen.

Pentru mediile liniare, izotrope si omogene relatiile electrostaticii au o forma mult simplificata. Astfel, legea lui Gauss, tinand cont de faptul ca permitivitatea este constanta, devine:

                    (I.108)

Ecuatia lui Poisson se scrie:

(I.109)

iar relatia (I.104) devine:

                     (I.110)

Deci, ecuatiile electrostaticii, pentru mediile liniare, izotrope si omogene, au aceeasi forma ca in vid. Putem spune acum ca vidul este un mediu dielectric liniar, izotrop si omogen.

b. Dielectrici anizotropi

In dielectricii studiati pana acum vectorii , si sunt paraleli. In general, nu este necesar ca cei trei vectori sa aiba aceeasi orientare. Mediile dielectrice, in care intensitatea campului electric, inductia electrica si polarizarea nu au aceeasi directie se numesc neizotrope. In mod obisnuit, sunt anizotropi dielectrici monocristalini (cu exceptia dielectricilor ce cristalizeaza in retele cu simetrie cubica, ce se comporta ca si mediile izotrope).

Si unele substante amorfe sau aflate in stare lichida pot deveni neizotrope daca sunt actionate de forte mecanice sau daca se afla in campuri electrice sau magnetice (toate aceste aspecte vor fi tratate pe larg in cursul de optica).

In asemenea dielectrici anizotropi, relatia dintre vectorii si este:

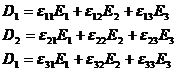    (I.111)

Dupa cum se observa, in aceste cazuri, permitivitatea electrica este un tensor de ordinul 2.

c.Discontinuitatea vectorilor si la suprafata de separatie a doi dielectrici polarizati

O importanta deosebita o prezinta comportarea vectorilor _{si la suprafata de separatie a doi dielectrici. Vom studia aceasta problema la suprafata de separatie a doi dielectrici liniari si izotropi.}

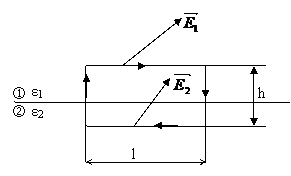
_{Fig. 70 - Campul electric in apropierea suprafetei de separatie a doi dielectrici.}

_{Presupunem ca h este un infinit mic de ordin superior in raport cu 1. Circulatia campului electric de-a lungul conturului, este:}

deci:

          (I.112)

La suprafata de separatie a doi dielectrici, componenta tangentiala a intensitatii campului electric este aceeasi de o parte si de alta a suprafetei de separatie.

Sa studiem polarizarea celor doua medii in apropierea suprafetei de separatie (vezi figura 71). Fie densitatea sarcinilor reale la suprafata de separatie si densitatile sarcinilor superficiale fictive de la suprafata de separatie. Presupunem ca h este un infinit mic de ordin superior in raport cu 1. In conformitate cu legea lui Gauss:

rezulta:

                                (I.113)

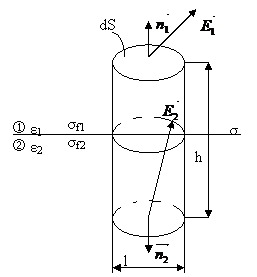
Fig. 71 - Polarizarea la suprafata de separatie a doi dielectrici

Dupa cum rezulta din formula (I.113), componenta normala a vectorului intensitate a campului electric sufera un salt la trecerea de la un dielectric la altul.

Relatia (I.113) poate fi scrisa si astfel:

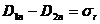                                  (I.114)

Modificarea componentei normale a inductiei campului electric, la trecerea de la un dielectric la altul, este egala cu densitatea superficiala de sarcina reala de pe suprafata de separatie dintre cei doi dielectrici.

Datorita modificarii vectorului intensitate electrica, la suprafata de separatie dintre dielectrici liniile de camp sufera o "frangere". Fie situatia din figura 72.

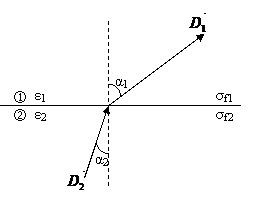
Fig. 72 - Modificarea directiilor liniilor inductiei electrice la trecerea dintr-un dielectric in altul.

Presupunem densitatea de sarcina superficiala reala egala cu 0. Din figura 72 rezulta ca:

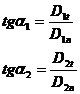
Tinand cont si de formula (I.114) si cum:

rezulta:

                  (I.115)

In concluzie, daca la limita de separatie a doi dielectrici izotropi si liniari, ajunge un camp electric, in conditiile in care nu exista sarcina reala, rezulta urmatoarele relatii de legatura pentru componentele vectorilor si _:

                              (I.116)

Importanta vectorului _{consta in faptul ca liniile de camp ale acestuia nu se intrerup la trecerea prin suprafata de separatie a doi dielectrici in lipsa sarcinilor reale; in aceleasi conditii liniile campului} sunt intrerupte. Un alt motiv ce justifica introducerea vectorului _{este sa se elimine necesitatea de a lua in considerare in mod explicit vectorul polarizare , care este legat de sarcinile de polarizare, (inaccesibile).}

_{d. Energia campului electrostatic in dielectrici}

Fie un dipol, _{, intr-un camp electric extern. Energia dipolului in campul electric extern este egala cu suma energiilor sarcinilor dipolului:}

                      (I.117)

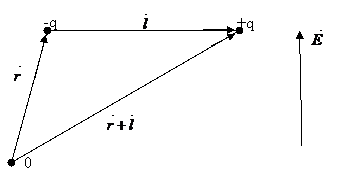
Fig. 73 - Interactiunea dintre un dipol si un camp electric

Dezvoltand in serie potentialul in raport cu , rezulta:

Oprindu-ne cu dezvoltarea la termenii de ordinul 1, obtinem:

Formula (I.117), devine:

                              (I.118)

Momentul electric dipolar, al unui element de volum dv, dintr-un dielectric va inmagazina energia:

dW_dip=-          (I.119)

Energia totala inmagazinata in interiorul dielectricului este integrala releatiei (I.119). Presupunand ca mediul dielectric este liniar si izotrop, obtinem:

W_dip=

Energia inmagazinata in campul electric din interiorul dielectricului considerat este:

Variatia energiei inmagazinate in campul electric prin introducerea dielectricului este:

(I.120)

Evident:

(I.121)

Energia suplimentara inmagazinata in domeniul spatial in care se introduce dielectricul fata de situatia in care in acest domeniu nu s-ar afla substanta este:

(I. 122)

e. Condensatorii in prezenta dielectricilor

Fie condensatorul plan paralel din figura 74.

Fig. 74 - Condensatorul plan paralel avand ca mediu izolator vidul.

Dupa cum stim, capacitatea acestui tip de condensator este data de formula (I.77).

Sa presupunem ca incarcam condensatorul electric cu sarcina superficiala s. Sarcina de pe armaturi va crea intre placile condensatorului un camp electric uniform de intensitate:

E₀= (I.123)

Introducand intre armaturile condensatorului, un dielectric acesta se va incarca cu o sarcina superficiala fictiva (vezi figura 75).

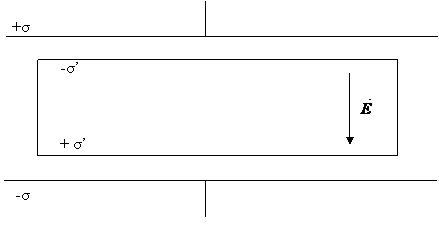
Fig. 75 - Condensatorul plan paralel avand ca mediu izolator un dielectric.

Conform celor spuse anterior, sarcinile fictive vor produce un camp electric de intensitate:

E'=-                       (I.124)

Intensitatea campului electric total dintre armaturi va fi:

E=E₀+E'=E₀-                        (I.125)

Dupa cum se vede, intensitatea campului electric dintre armaturi, in prezenta dielectricului, este mai mica decat in vid. Acest lucru poate fi pus in evidenta prin masurarea tensiunii de la bornele condensatorului. Se poate observa experimental ca tensiunea scade prin introducerea dielectricului.

Conform formulelor (I.105) si (I.124) rezulta:

                               (I.126)

Inlocuind acest rezultat in (I.125) obtinem:

E=

Diferenta de potential dintre placi va fi:

V=Ee=

Inlocuind acest rezultat in formula fundamentala a condensatorilor avem:

C=

Sau:

C=                                      (I.127)

Constatam ca si in cazul in care intre placile condensatorului se afla un dielectric formula capacitatii condensatorului plan are aceeasi forma ca in vid. Acelasi rezultat se obtine si in cazul altor geometrii ale condensatorului. Deoarece permitivitatea absoluta a dielectricului este mai mare decat cea a vidului, rezulta ca si capacitatea condensatorilor intre armaturile carora se afla dielectrici este mai mare decat in cazul in care intre placi nu s-ar afla nimic.

f. Relatia Clausius - Massotti

Un dielectric este caracterizat, la nivel macroscopic, de permitivitatea electrica e iar la nivel microscopic de polarizabilitatea moleculara a. Vrem sa determinam o relatie intre acesti parametri. Vom analiza cazul dielectricilor liniari, izotropi si omogeni iar, pentru a simplifica problema, ne vom referi la cazul polarizarii uniforme.

Deoarece densitatea de sarcina fictiva este data de relatia (I.94) rezulta, in cazul polarizarii uniforme, ca aceasta este nula. Vor ramane numai sarcini fictive superficiale.

Dupa cum stim, momentul electric dipolar al moleculelor este dat de relatia de la paragraful I.6.c. Pentru a - l afla pe sa practicam, fictiv o cavitate sferica a carei raza este de acelasi ordin de marime cu distanta intermoleculara. Vom scoate molecula din interiorul cavitatii si vom determina intensitatea campului electric in centrul ei. Campul electric din centrul sferei poate fi scris astfel:

=++                   (I.128)

unde este campul electric aplicat din exterior, este campul electric produs de sarcinile electrice de polarizare de pe suprafata dielectricului, este campul electric produs de sarcinile de polarizare de pe suprafata sferei. Pentru a - l calcula pe sa consideram figura 76.

Fig. 76. - Referitor la calculul campului electric in interiorul unei cavitati circulare din interiorul unui dielectric.

Densitatea de sarcina electrica superficiala de pe pereti sferei este: σ_fi=-Pcosq

Pe elementul de suprafata al sferi se va afla sarcina:

dQ=σ_fir²dS

Aceasta sarcina va crea in O, pe axa oz, campul:

dE_z=-

Campul electric total pe axa Oz este:

E_z=

Deci, in general:

Notand cu: =+ campul electric produs de sarcinile aflate la distanta mare de O, rezulta:

                     (I.129)

Acest camp produce polarizarea atomului din centrul sferei. Daca in unitatea de volum se gasesc n atomi, vectorul polarizare al dielectricului va fi:

Notand cu M masa molara, cu r densitatea si cu N_A numarul lui Avogadro, rezulta:

N_A=

Tinand cont de relatia precedenta, exprimand polarizarea prin susceptibilitate si aceasta din urma prin permitivitate, rezulta:

                   (I.130)

Ecuatia (I.130) se numeste relatia Clausius - Massotti. Marimea se numeste polarizabilitate moleculara. In functie de natura proceselor care determina momentul dipolar al moleculei, polarizabilitatea moleculara depinde de inversul temperaturii absolute, asa cum se vede in figura 7

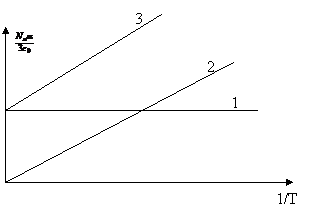
Fig. 7 Dependenta polarizabilitatii moleculare de inversul temperaturii absolute.

Dreapta 1 corespunde dielectricilor pur nepolari. Dreapta 2 corespunde dielectricilor polari a caror polarizabilitate electronica este neglijabila. Dreapta 3 corespunde unui dielectric in care au loc ambele tipuri de polarizare.

Asemenea reprezentari grafice, realizate pe baza datelor experimentale, permit sa se determine si momentul dipolar .

g. Aplicatii

Problema 1

Sa se calculeze campul electric in interiorul si exteriorul unei sfere de raza r, uniform polarizate in absenta unui camp electric extern.

Campul electric creat de o sfera polarizata intr-un punct exterior sferei este egal cu campul electric dat de un dipol de moment =, plasat in centrul sferei. este polarizarea dielectrica.

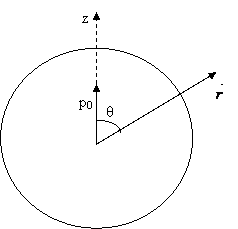
Fig.78. Referitor la problema 1.

Potentialul in toate punctele frontierei sferice este:

Cum rcosθ z, rezulta:

Intensitatea campului electric in interiorul sferei este:

Deci:

Campul exterior va fi:

sau:

Problema 2

Sa se calculeze potentialul electric intr-un punct exterior al unei coloane din material uniform polarizat cu intensitatea de polarizare . Suprafata sectiunii transversale a coloanei este S iar coordonatele coloanei sunt z₁ si z₂.

Un element al cilindrului de inaltime dz are un moment dipolar . Contributia sa la potentialul din punctul M este:

Potentialul intregii coloane va fi:

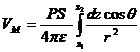
Cum dzcosθ=-dr, rezulta:

Fig. 79 Referitor la problema 2.