Memorii asociative bidirectionale

MEMORII ASOCIATIVE BIDIRECTIONALE

1. Notiuni de baza

O retea asociativa bidirectionala (Kosko, 1987) este o retea neuronala ce consta din doua straturi de neuroni complet interconectate. Doi neuroni din acelasi strat nu sunt interconectati, insa fiecare neuron poate avea (sau nu) o legatura cu

el insusi. Toate conexiunile interneuronale sunt bidirectionale. Informatia circula intre cele doua straturi, in ambele sensuri. Daca dinamica straturilor conduce la o comportare de ansamblu stabila a retelei, atunci structurile de acest tip se numesc memorii asociative bidirectionale (MAB).

Fie F_x si F_y cele doua straturi si W matricea ponderilor conexiunilor de la campul F_y la campul F_x. Matricea ponderilor conexiunilor spre campul F_x este W^T. Exista trei tipuri de memorii asociative:

1. Memorii asociative interpolatorii.

Aceste memorii realizeaza o functie A, astfel incat

A(Rⁱ) = Sⁱ, i=1,2 ,p.

Daca vectorul de intrare R difera de unul din vectorii R' printr-un vector D, adica avem

R = Rⁱ + D ,

atunci iesirea memoriei difera de S' printr-un anumit vector E :

A(Rⁱ + D) = Sⁱ + E .

Memorii heteroasociative.

Memoriile heteroasociative realizeaza o functie A, astfel incat

Daca R este mai apropiat (in sensul distantei Hamming) de R', adica

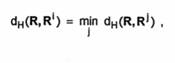
atunci avem

A(R) = Sⁱ.

3. Memorii autoasociative.

in cazul memoriilor autoasociative, in multimea de instruire formele asociate coincid cu formele cheie, adica

Sⁱ = Rⁱ, i = 1,2 p.

Memoriile de acest fel realizeaza o functie A pentru care

A(Rⁱ) = Rⁱ, i = 1,2 p.

Daca R este un vector pentru care

atunci

Asociatorul Liniar

Consideram multimea de instruire compusa din perechile

(x¹,y¹), (x²y²) (xP.yP),

unde x' e Rⁿ si y' e R^m. Ca de obicei, vom considera ca xⁱ si yⁱ sunt vectori coloana si presupunem ca vectorii xⁱsunt ortonormati:

Si

Aceste conditii se mai pot scrie sub forma

unde 5 este simbolul lui Kronecker.

In acest caz, putem construi o memorie interpolatorie definind functia

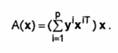
Vectorii fiind ortonormati, avem

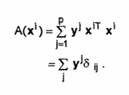
Am obtinut, deci

Daca x este un vector astfel incat

atunci iesirea corespunzatoare este

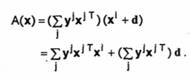
Cu notatia

iesirea retelei se mai poate scrie

Acest mecanism de memorare a listei de asociere

poate fi considerat drept o varianta a legii de invatare a lui Webb si se numeste regula produsului exterior.

Se pune in mod natural intrebarea, ce ponderi trebuie sa aiba reteaua, pentru ca ea sa realizeze functia A. Examinand expresia acestei functii, rezulta ca putem defini ponderile asociatorului liniar ca fiind elementele unei matrici W, unde

Se observa ca matricea ponderilor este suma matricelor de corelatie ale formelor din multimea de instruire.

Fie r un neuron din campul de iesire F_y si s un neuron din campul de intrare F_x. Ponderea w_rs a conexiunii (r, s) se va scrie

Functia A se poate scrie, acum, sub forma

Sa notam ca W nu este, de regula, simetrica. Ponderea conexiunii (r, s) nu este, deci, egala cu cea a conexiunii (s, r):

Notam cu X matricea (n x p), avand pe coloana i componentele vectorului x': X = (x¹ x² xP) .

Notam, de asemenea, cu Y matricea (m x p) ce are pe coloana i vectorul yⁱ

Y = (y¹ y² ... yP).

Cu aceste notatii, matricea W a ponderilor conexiunilor se va scrie sub forma

3. Functionarea Asociatorului Liniar

Dupa calcularea matricei W, daca retelei asociative i se prezinta vectorul de intrare x, ea va genera vectorul de iesire y, unde

Tinand cont de forma matricei W, iesirea retelei se scrie

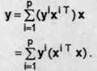
Se observa ca iesirea y a retelei neuronale este o combinatie liniara a vectorilor

Coeficientii acestei combinatii liniare sunt produsele scalare

Din acest motiv, o astfel de retea se numeste Asociator liniar.

Consideram, acum, un caz particular de asociator liniar. Daca formele fiecarei asociatii coincid, adica daca avem

yⁱ = xⁱ, i = 1, 2 p ,

atunci obtinem o retea numita Autoasociator liniar. In acest caz, matricea W a conexiunilor este suma matricelor de autocorelatie corespunzatoare vectorilor de instruire

Avem, deci

In general, un autoasociator este o retea instruita sa reproduca elementele unei multimi de invatare

Daca retelei i se prezinta vectorul xⁱ, se doreste ca, dupa cateva iteratii (sau chiar dupa una singura), iesirea retelei sa fie, de asemenea, xⁱ. Astfel, reteaua a memorat (codificat) multimea de instruire.

Este interesant de remarcat in cazul autoasociatorilor, ca si al oricarei memorii, comportarea acestora cand li se prezinta intrari ce difera usor de exemplele de instruire deja memorate. Daca intrarea este apropiata (in sensul unei anumite distante) de x', atunci reteaua tinde sa reproduca forma x'. Rezulta, astfel, ca autoasociatorii pot fi considerati ca fiind memorii adresabile prin continut. Exemplele de instruire memorate reprezinta cunostinte invatate (ce pot fi considerate drept 'amintiri'). Autoasociatorul va fi capabil sa regaseasca o informatie completa, pornind de la elemente partiale (incomplete) sau de la versiuni distorsionate ale respectivei informatii.

Aceasta discutie poate fi extinsa si la modele mai generale de memorii implementate cu retele neuronale, consideratiile precedente ramanand valabile.

Revenind la Asociatorul liniar, sa notam ca acesta nu implica nici o instruire. Matricea W a ponderilor se calculeaza pornind de la formele multimii de invatare si aceasta matrice nu se modifica in cursul functionarii retelei.

De asemenea, Asociatorul liniar prezinta fenomenul de regasire perfecta ('perfect recall'):

Daca vectorii xⁱ nu mai sunt ortogonali, regasirea cu regula Webb considerata (legea produsului exterior) nu mai este perfecta.

Deoarece vectorii xⁱ sunt din Rⁿ, rezulta ca exista cel mult n vectori reciproc ortogonali. Aceasta inseamna ca n este numarul maxim de vectori ce pot fi memorati cu regasire perfecta, folosind algoritmul de invatare bazat pe regula Webb considerata.

O alta regula de regasire se poate defini folosind produsul boolean a doi vectori. Sa admitem ca vectorii xⁱ si yⁱ au componentele 0 si 1. n acest caz, matricea W se defineste ca

unde cuam notat suma booleana. Rezulta ca ponderea conexiunii (i, j) se va scrie

4. Memorii Liniare Optimale

In cazul in care vectorii xⁱ nu sunt ortonormali, putem sa definim o masura a erorii Asociatorului liniar. Daca rⁱ este iesirea reala a asociatorului si yⁱ este iesirea dorita, se defineste eroarea asociata perechii (xⁱ, xⁱ) ca fiind

Eroarea totala E este suma erorilor corespunzatoare celor p vectori de intrare. Avem, deci

Putem deduce ca matricea W a ponderilor pentru care aceasta eroare este minima are forma

unde X⁺ este pseudoinversa matricei X. Daca X are p coloane liniar independente, atunci pseudoinversa sa este

X⁺ = (X^TX⁾'¹X^T.

Memoriile asociative liniare optimale sunt retele in care ponderile sunt date de matricea W ce minimizeaza eroarea E. Algoritmul recursiv al lui Greville furnizeaza o metoda iterativa eficienta pentru calculul pseudoinversei.